1.1. Корректность по Адамару

Ж.Адамар определил два условия, которым должна удовлетворять корректно поставленная краевая (начально-краевая) задача для уравнений с частными производными: существование и единственность решения [1, c.12]. Вместе с тем хорошо известно о третьем условии корректности по Адамару в отношении непрерывной зависимости решения от данных задачи. Действительно, он уделил пристальное внимание исследованию этого аспекта применительно к теореме Коши-Ковалевской, посвященной решению дифференциального уравнения

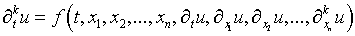(1.1)

(системы аналогичных уравнений), где f – аналитическая функция своих аргументов в окрестности начала координат, с начальными условиями

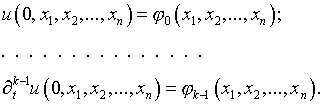(1.2)

Как отметил Ж.Адамар, при рассмотрении задачи (1.1), (1.2), носящей имя Коши, возникают три следующих вопроса [1, c.17]:

• Имеет ли она решение?
• Является ли решение единственным? (В совокупности, корректно ли поставлена задача?).
• Наконец, как вычислить это решение?

Теорема Коши-Ковалевской (в ее авторской интерпретации) утверждает, что, за исключением ряда особых случаев, указанная задача имеет единственное решение, аналитическое вблизи начала координат. При этом функции
j ₀, … , j _k-1 в (1.2) могут быть не только аналитическими, но и регулярными, то есть непрерывными со своими производными до некоторого порядка. Подразумевается известная возможность равномерного приближения j ₀, … , j _k-1 рядами Тейлора по степеням x₁, … , x_n на которые переносятся все операции с аналитическими функциями, включая дифференцирование до соответствующего порядка.

Однако такой подход встретил резкую критику Ж.Адамара. По его мнению, вопрос заключается не в том, насколько подобная аппроксимация влияет на начальные данные, главное – как значительно в результате изменится решение? Подчеркнута неэквивалентность понятий малого возмущения для данных задачи Коши и ее решения [1, c.39]. В этой связи Ж.Адамар привел свой знаменитый пример о решении дифференциального уравнения

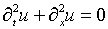(1.3)

с условиями

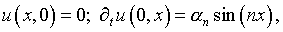(1.4)

где a _n – функция, быстро убывающая с ростом n.

Выражение в правой части (1.4) может быть сколь угодно малым и тем не менее приведенная задача имеет решение

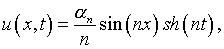(1.5)

которое, если a _n = 1/n или 1/nm , или 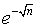, весьма велико для любого значения t, отличного от нуля (вследствие превалирующего роста 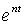и соответственно 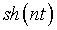). Итак, функция (1.5) не зависит непрерывно от начальных данных и, следовательно, задача (1.3), (1.4) является некорректной.

О регулярности правых частей (1.2) Ж.Адамар заметил: “… поистине один из наиболее любопытных фактов теории заключается в том, что уравнения, по виду очень близкие, ведут себя совершенно противоположным образом” [1, c.29].

Вопросам корректной постановки задач Коши посвящено трудно обозримое количество исследований, авторы которых занимались как выделением соответствующих классов дифференциальных уравнений, так и минимизацией ограничений, предъявляемых к начальным условиям (см. [2]). Однако нас более всего интересует собственно характер зависимости решения от данных задачи и с этой точки зрения классическое утверждение Ж.Адамара: “Аналитическая задача всегда корректно поставлена в смысле, указанном ранее, когда есть механическое или физическое истолкование вопроса” [1, c.38].

Как отметили В.Я.Арсенин и А.Н.Тихонов [3], последнее поставило под сомнение целесообразность изучения некорректных задач, к которым авторы отнесли: решение интегральных уравнений первого рода; дифференцирование функций, известных приближенно; численное суммирование рядов Фурье, когда их коэффициенты известны приближенно в метрике l₂; аналитическое продолжение функций; решение обратных задач гравиметрии, а также плохо обусловленных систем линейных алгебраических уравнений; минимизацию функционалов в условиях несходящихся последовательностей координатных элементов; некоторые задачи линейного программирования и оптимального управления; проектирование оптимальных систем и, в частности, синтез антенн. Подчеркнуто, что это далеко не полный перечень, так как некорректные задачи возникают при исследовании широчайшего спектра проблем физики и техники.

Г.Е.Шилов в выступлении на заседании Московского математического общества, посвященном памяти Ж.Адамара [4], высказал следующее: “Наше время внесло коррективы в установки Адамара, поскольку выяснилось, что некорректные по Адамару задачи могут быть содержательными (как, например, задача о восстановлении потенциала поля по данным рассеяния); но, конечно, изучение корректных задач, провозглашенное Адамаром, явилось цементирующим средством для формирования всей теории” (имеется в виду функци-ональный анализ). Данная цитата заимствована из биографического очерка Е.М.Полищука и Т.О.Шапошниковой [5], в котором также отмечено, что с течением времени мнение Ж.Адамара о важности для практики только корректных задач стали понимать не столь абсолютно.

Вместе с тем делались и достаточно резкие заявления:

“Более того, Адамар выдвинул утверждение о том, что некорректные задачи вообще не имеют смысла. А поскольку (как это видно с современных позиций) большинство прикладных задач, описываемых уравнениями первого рода, являются некорректными, то данное утверждение выдающегося математика, по-видимому, сильно затормозило в 20–50 гг. ХХ века развитие теории, методов и практики решения указанного класса задач” [6, c.12].

“До последнего времени считалось, что некорректные задачи лишены физического смысла и их не имеет смысла решать. Однако имеется много важных прикладных задач физики, техники, геологии, астрономии, механики и т.д., математически описываемых адекватно и тем не менее являющихся некорректными, что сделало актуальной проблему разработки эффективных методов их решения” [6, c.225] *.