1.3. Теорема Банаха об обратном операторе в аспекте корректности

Приведем выдержку из [5, c.175]: “Первоначально Адамар определял корректность задачи лишь условиями разрешимости и единственности, энергично настаивая на непрерывной зависимости решения от начальных данных только при обсуждении задачи Коши. Вот что он написал в книге “Теория уравнений в частных производных”, вышедшей в Пекине через год после его смерти: “Это третье условие, которое мы ввели в “Лекциях о задаче Коши …”, но не рассматривали как часть определения хорошо поставленных задач, было присоединено, и совершенно справедливо, Гильбертом и Курантом [12]. Мы принимаем здесь их точку зрения”.

Е.М.Полищук и Т.О.Шапошникова сопроводили этот текст комментарием [5, с.175–176]: “С математической точки зрения вопрос о необходимости включения требования непрерывности решения относительно данных представляется довольно деликатным. Дело в том, что согласно известной теореме Банаха о замкнутом графике, однозначная разрешимость линейной задачи влечет ограниченность обратного оператора, а тем самым – и непрерывную зависимость решения от правых частей”. Отмечено, что на решение задачи могут также влиять вариации коэффициентов дифференциальных уравнений и контура рассматриваемой области, вследствие чего использование трех условий корректности является предпочтительным.

Вместе с тем к рассматриваемой проблематике в большей мере относится теорема Банаха об обратном операторе [20, c.34–36], являющаяся следствием указанной выше. Ее формулировка, данная А.Н.Колмогоровым и С.В.Фоми-ным, гласит [21, c.259–260]: Пусть А – линейный ограниченный оператор, взаимно однозначно отображающий банахово пространство В₁ на банахово пространство В₂. Тогда обратный оператор А^-1 ограничен.

Л.А.Люстерник и В.И.Соболев [22, c.159–161] в дополнение подчеркнули, что подразумевается взаимно однозначное отображение всего банахова пространства В₁ на все банахово пространство В₂. Наряду с этим оговорена ситуация, при которой “… оператор, обратный к ограниченному линейному оператору, оказывается хотя и линейным, но определенным не на всем пространстве В₂, а лишь на некотором линейном многообразии и неограниченным на этом многообразии”.

Несколько иная трактовка той же теоремы в [23, c.60] сводится к следующему: Если линейный ограниченный оператор А, отображающий банахово пространство В₁ на все банахово пространство В₂, имеет обратный – А^-1, то А^-1 ограничен. При этом отмечено, что данное утверждение утрачивает силу, если отказаться от полноты одного из указанных пространств. 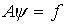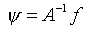Содержится также пояснение: из существования и единственности решения уравнения при всякой правой части из В₂ следует непрерывная зависимость решения от .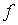

Л.В.Канторович и Г.П.Акилов внесли дополнение, касающееся отображения в обозначенных условиях на замкнутое подпространство банахового пространства В₂ [24, c.454]. Суть в том, что замкнутое подпространство банахова пространства само является банаховым пространством.

С.Г.Михлин привел доказательство теоремы [25, c.507]: Для того, чтобы линейная задача 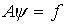была корректной в паре банаховых пространств В₁, В₂, необходимо и достаточно существование ограниченного оператора А^-1. отображающего все пространство В₂ на В₁. При этом автор четко разграничил категории существования и единственности решения краевой задачи с ее корректностью в целом, предполагающей как следствие непрерывность зависимости от данных (третье условие по Адамару). В этой связи характерно определение: “Краевая задача называется корректной в паре банаховых пространств В₁ и В₂, если ее решение единственно в В₁ и существует при любых данных из В₂ и если достаточно малому изменению начальных данных в норме В₂ соответствует сколь угодно малое изменение решения в норме В₁” (с.204).

Подчеркнуто, что рассматриваемая задача может оказаться корректной в одной паре пространств и некорректной в другой. При этом некорректность интегрального уравнения Фредгольма первого рода (1.6) установлена от противного: если задача корректна – существует ограниченный оператор А^-1 и, следовательно, тождественный оператор I = A^-1A вполне непрерывен в соответствующем бесконечномерном пространстве, что противоречит положениям общей теории [23]. С.Г.Михлин также вполне благосклонно отметил направление приближенного решения некорректных задач, возглавляемое А.Н.Тихоновым.

В аналогичном по содержанию курсе [26] С.Г.Михлин повторил приведенные формулировки, однако А.Н.Тихонов не упомянут вовсе, тогда как обсуждение уравнения (1.6) получило весьма интересное развитие (с.171). Показано как задача его разрешения становится корректной, если пару пространств В₁, В₂ заменить на такую, в которой оператор А уже не будет вполне непрерывным. Общие соображения проиллюстрированы следующим примером. Пусть 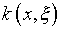и 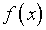удовлетворяют условиям из п.1.2, включая (1.7). Тогда по теореме Пикара решение уравнения (1.6) имеет вид

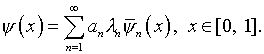(1.10)

Оказывается, если в качестве В₁ сохранить 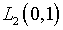, а В₂ принять также гильбертовым пространством функций, нормированных согласно (1.7), то есть – l₂, решение уравнения (1.6) превращается в корректно поставленную задачу и соответственно оператор А^-1 – ограничен.

Спустя еще одно десятилетие, С.Г.Михлин фактически отказался от исследований, связанных с проблемой корректности [27]: “Автор придерживается классической точки зрения, по которой задача, к решению которой применяются математические методы, должна рассматриваться как поставленная точно. Конечно, существуют и другие мнения (с.7) … Тем самым мы пренебрегаем так называемыми неустранимыми погрешностями, связанными с постановкой упомянутой задачи как задачи естествознания или социально-научных дисциплин (погрешности измерений, недостаточная точность основных гипотез и т.п.)” (с.17).

М.М.Лаврентьев и Л.Я.Савельев охарактеризовали исследование вопроса о разрешимости уравнения (1.6) с привлечением соображений типа [26] как тривиальное, поскольку при экспериментальном определении 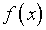трудно представить, чтобы соответствующая погрешность оказалась малой в норме пространства l₂ [28, c.217]. Наряду с этим отмечено, что, вообще говоря, для любого операторного уравнения можно подобрать пары пространств, в которых задача его разрешения была бы корректной.

Г.М.Вайникко и А.Ю.Веретенников обратили внимание на сложность описания таких пространств. Более того, даже интегральное уравнение Вольтерра первого рода



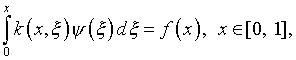
допускающее регуляризацию



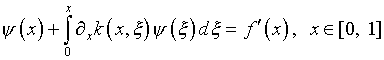
и элементарно разрешимое в квадратурах, по соображениям нормы для зачастую приходится рассматривать как некорректно поставленную задачу [29, c.6].

В отношении пары пространств, реализующих условия корректной постановки, представляет интерес оригинальное замечание К.И.Бабенко [30, c.304]: “Известный пример Адамара (1.3), (1.4), дающий решение задачи Коши вида (1.5), говорит вовсе не об отсутствии непрерывной зависимости от начальных данных, как его обычно трактуют, а о том, что малые изменения начальных данных могут привести к тому, что мы выходим из совокупности начальных данных, для которых существует решение задачи Коши”. Кстати, Р.Рихтмайер продемонстрировал корректность процедуры численной реализации весьма сложной задачи указанного типа с представлением искомых функций двумерными степенными рядами и использованием специальных приемов подавления погрешностей арифметических операций [31, п.17.В].

В контексте настоящего изложения представляют также интерес две теоремы, приведенные В.А.Треногиным [32, c.225]:

Пусть Е₁ и Е₂ – бесконечномерные нормированные пространства, причем Е₂ полно. Если А – вполне непрерывный линейный оператор из Е₁ в Е₂, отличный от конечномерного, то его область значений 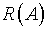не является замкнутым множеством в Е₂.

Пусть А – вполне непрерывный оператор из бесконечномерного нормированного пространства Е₁ в нормированное пространство Е₂, причем 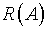на существует обратный оператор А^-1. Тогда А^-1 неограничен на 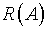.