| |
|
|
|
2.2. Краткий экскурс в развитие обозначенных концепций
2.4. Обратные задачи для дифференциальных уравнений математической
физики
2.5. Альтернативные воззрения и разработки
2.6. Сопоставление основополагающих концепций А.Н.Тихонова
и В.М.Фридмана
2.7. Плохо обусловленные конечномерные задачи и вопросы дискретизации
2.8. Кризис технологии математического моделирования
Изложение настоящего подраздела основывается на монографии А.Н.Тихонова и В.Я.Арсенина [1], которую буквально пронизывает концепция адекватности некорректных постановок и, в частности интегральных уравнений первого рода, задачам математической физики. В качестве иллюстрации показано, что решение интегрального уравнения Фредгольма первого рода
 |
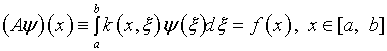(2.1) |
с
и 
непрерывными
по 
может
претерпевать сколь угодно значительные изменения, как в метрике 
так
и 
при
малых в 
вариациях
правой части, вида 
Ситуация с возмущением ядра 
по существу аналогична, в связи с чем авторы ставят вопрос: что следует понимать
под решением уравнения (2.1),
когда 
и 
известны приближенно? По их мнению, такая задача должна рассматриваться
как «недоопределенная» и соответственно для отбора возможных решений необходимо
привлекать дополнительную информацию о функции 
качественного, или же количественного характера, «которая обычно имеется». В
этой связи обратим внимание на соображения Н.Г.Преображенского относительно
системы линейных алгебраических уравнений, получаемых дискретизацией (2.1)
[2, c.130]:
«Анализ показывает, что выбирая достаточно высокий порядок приближения мы превращаем [указанную систему] в сколь угодно плохо обусловленную … . В этих условиях необходимо внесение в алгоритм какой-либо априорной нетривиальной дополнительной информации, с помощью которой только и можно надеяться отфильтровать вуалирующие ложные варианты и выделить решение, наиболее близкое к истинному. Любые чисто математические ухищрения, не привлекающие дополнительных априорных данных, эквивалентны попытке создания информационного perpetuum mobile, производящего информацию из ничего».
На априорной количественной информации базируется так называемый метод подбора
решения некорректно поставленных задач. Показано, что если компакт 
метрического пространства 
взаимно однозначно и непрерывно отображается на множество 
метрического пространства 
то обратное отображение
на
также непрерывно. Соответственно предположение о принадлежности
решения, в частности уравнения (2.1),
компакту
позволяет считать оператор 
на множестве 
непрерывным.
Практическая реализация сводится к аппроксимации
рядом с параметрами, изменяющимися в ограниченных пределах (так,
чтобы
представляло замкнутое множество конечномерного пространства),
которые находятся из условия минимизации невязки удовлетворения уравнению (2.1).
Отметим отсутствие сколько-нибудь общих рекомендаций в отношении выбора 
В свете изложенного, М.М.Лаврентьев сформулировал понятие корректности по Тихонову для уравнения (2.1) [3]:
1) Априори
известно, что решение этого уравнения 
существует
и принадлежит множеству пространства
2) Решение
единственно
на множестве
3) Оператор
непрерывен
на множестве 
пространства 
Если – компакт
(случай назван «обычным») последнее условие становится следствием предыдущих.
Задачи, в которых оператор
неограничен на множестве 
и множество возможных решений
не является компактом, названы существенно некорректными. Для них Тихонов выдвинул
идею построения регуляризирующего оператора
в некотором смысле близкого
к 
область значений которого при отображении из 
в
допускала бы согласование с правой частью уравнения (2.1),
известной приближенно. При этом 
должен содержать параметр регуляризации 
зависящий от точности исходной информации.
Оператор 
назван регуляризирующим для уравнения (2.1),
в случае если он обладает свойствами:
1) Определен для любых 
и
2) При 
где
и
–
соответствующие точные выражения, существует такое 
что
для любого 
найдется
Здесь
Подразумевается возможность выбора 
так,
что при 
регуляризированное
решение 
то
есть 
Вместе
с тем, отмечена алгоритмическая сложность построения зависимости для
которой оператор 
являлся
бы регуляризирующим, применительно к классам практически важных задач. Вопросам
разрешения данной ситуации посвящены многочисленные публикации последователей
Тихонова, о которых будет сказано ниже.
Непосредственно в [1],
построение
выполнено с привлечением аппарата вариационного исчисления, сводящего определение
к минимизации функционала
 |
(2.2) |
Для уравнения (2.1) его стабилизирующую компоненту рекомендовано использовать в виде
 |
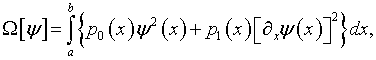(2.3) |
где
>= 0 – заданные функции.
В случае симметричного ядра
процедура минимизации (2.2)
эквивалентна решению интегро-дифференциального уравнения
 |
(2.4) |
при условиях
 |
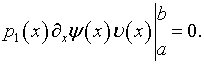(2.5) |
Здесь 
– произвольная
вариация функции 
не
выводящая ее из класса допустимых.
По мнению авторов [4], подавляющее большинство обратных задач являются некорректно поставленными, причем попытки их решения, ввиду огромной практической важности, предпринимались на протяжении длительного периода. «Но только в результате … появления фундаментальных работ академика А.Н.Тихонова была создана современная теория решения обратных задач, в основу которой легло понятие регуляризующего алгоритма» (с.7). Далее излагается процедура численной реализации интегральных уравнений Фредгольма первого рода, связанных с интерпретацией астрофизических наблюдений, путем выделения компакта возможных решений в классе монотонно ограниченных функций.
Как отметил О.А.Лисковец [5]: «… корректность по Тихонову достигается за счет сужения допустимого множества решений до класса корректности» (с.13). Представляет интерес также следующая цитата из указанной монографии: «В отличие от господствовавшего прежде мнения о том, что все задачи, описывающие физическую реальность, корректны, по современным представлениям каждая реальная задача регуляризуема, то есть имеет хотя бы один регуляризатор» (с.14).
Заключение В.А.Морозова [6, c.9]:
«Метод регуляризации А.Н.Тихонова оказался необременительным на практике, так
как не требовал фактического задания компакта М, в котором содержится искомое
решение уравнения (2.1).
… Основная трудность применения данного метода заключается в формулировке алгоритмических
принципов выбора параметра регуляризации 
». Из его же монографии [7,
c.4]: «Значимость статьи А.Н.Тихонова [8]
трудно переоценить. Она послужила толчком для выполнения целого ряда работ других
исследователей в самых различных областях математического анализа и естествознания:
спектроскопии, электронной микроскопии, идентификации и автоматическом регулировании,
гравиметрии, оптике, ядерной физике, физике плазмы, метеорологии, автоматизации
научных исследований и ряде других разделов науки и техники».
Мнение В.В.Воеводина [9, с.43]: «Успех применения метода регуляризации к решению неустойчивых систем алгебраических уравнений объясняется в значительной мере тем, что А.Н.Тихонов и его последователи не ограничились исследованиями отдельных фрагментов этой сложной задачи, а рассмотрели весь комплекс связанных с ней вопросов. Это в первую очередь четкая постановка самой задачи, построение устойчивого к возмущению входных данных алгоритма ее решения, разработка эффективного численного метода, получение оценок отклонения реально вычисляемого объекта от искомого в зависимости от возмущения входных данных и ошибок округления».
Из предисловия к сборнику статей [9] А.А.Самарского и А.Г.Свешникова: «Фундаментальное значение для всей современной математики имеет выяснение Андреем Николаевичем Тихоновым роли некорректных задач в классической математике и ее приложениях (обратные задачи). Им предложен принципиально новый подход к этому классу задач и развиты методы построения их устойчивых решений, основанные на принципе регуляризации».
Результаты исследований, посвященных установлению параметра регуляризации
подытожены в [10]. В
предположении о том, что погрешности определения свободного члена 
и ядра
уравнения (2.1) известны,
используются различные принципы минимизации невязки вида
При этом, вычисление параметра как
корня соответствующего уравнения не вызывает затруднений, однако выбор 
по
существу, сопряжен со значительной неопределенностью. Главное препятствие состоит
в том, что весьма проблематичной является достоверная оценка погрешности, обусловленной
«мерой несовместности» конкретно рассматриваемого уравнения 
Значительные усилия предпринимались с целью сокращения объема информации,
необходимой для вычисления параметра
. Заметный шаг в этом направлении сделан А.Н.Тихоновым и В.Б.Гласко, предложившими
критерий минимизации по
функционала 
[11] (см. также [1,
п.2.7]), однако его теоретическое обоснование оказалось возможным лишь для сравнительно
узких классов задач. Ряд способов определения
связан с использованием решений уравнения (2.1)
для функций
специального вида.
В [10] освещено
также состояние исследований по оценке точности методов решения интегрального
уравнения (2.1). При этом
в случае принадлежности
компакту серьезных осложнений, как правило, не возникает, и основной интерес
представляют алгоритмы регуляризации. Если в (2.3)
и параметр
– конечен, (2.4)
становится интегральным уравнением Фредгольма второго рода, на которое, в предположении
известной погрешности определения
и 
распространяется общая теория приближенных методов Л.В.Канторовича [12,
п.14.1].*
Вместе с тем, как показал В.А.Винокуров [13],
при отсутствии априорной информации о решении уравнения (2.1),
оценка погрешности вычисления
средствами регуляризации принципиально неосуществима. Правомерно лишь ставить
вопрос о сходимости вычислительной процедуры, или же регуляризуемости соответствующей
задачи.
Отметим в этой связи высказывание А.Б.Бакушинского и А.В.Гончарского [14,
c.13]: «К сожалению, в общем случае невозможно оценить меру близости
к 
без дополнительной информации о решении уравнения (2.1).
Это характерная особенность некорректных задач. В общем случае регуляризирующий
алгоритм гарантирует лишь асимптотическую сходимость приближенного решения к
точному при
».
С именем М.М.Лаврентьева связывают случай практической реализации метода Тихонова, состоящий в упомянутом выше сведении задачи (2.4), (2.5) к решению интегрального уравнения Фредгольма второго рода
 |
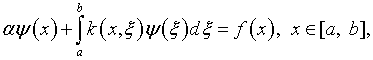(2.6) |
где
– малый
параметр.
Показано, что 
при
и 
Здесь
–
погрешность определения ядра 
аналогичная
(см.
п.2.1).
Метод В.К.Иванова [15]
позволяет находить так называемое квазирешение, минимизирующее невязку удовлетворения
(2.1) для класса функций
где 
– компакт. Квазирешение уравнения (2.1)
на таком компакте имеет вид:
 |
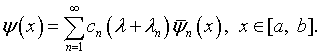(2.7) |
Здесь
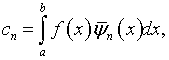
где
и 
– соответственно
характеристические числа и собственные функции ядра 
параметр
и представляет
положительный корень уравнения
 |
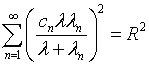(2.8) |
при условиях соответственно
 |
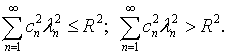(2.9) |
Специальные методы регуляризации разработаны для ситуаций, в которых о решении уравнений вида (2.1) имеется значительный объем информации статистического характера (спектральные плотности, математические ожидания и т.п.). Так, В.Н.Вапник [16] вполне конструктивно использовал специфику задач о распознавании образов, связанную с неоднозначностью и вследствие этого экстремальным поведением искомых функций. Обращает внимание содержащееся в указанной монографии определение (с.8), которое, по всей видимости, подразумевалось многими, однако не находило столь отчетливой формулировки:
«Задача восстановления зависимостей по эмпирическим данным была и, вероятно, всегда будет центральной в прикладном анализе. Эта задача является математической интерпретацией одной из основных проблем естествознания: как найти существующую закономерность по разрозненным фактам».
Пусть
– симметричное положительно определенное ядро и уравнение (2.1)
разрешимо. Тогда, как показал В.М.Фридман [17],
последовательность функций, определяемых итерациями
 |
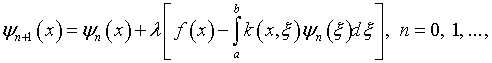(2.10) |
сходится в 
к решению уравнения (2.1)
при произвольном выборе начального приближения 
и 
где 
– наименьшее характеристическое число ядра 
М.А.Красносельский [18]
распространил данный результат на любое имеющее решение уравнение вида (2.1)
с линейным ограниченным оператором 
в гильбертовом пространстве 
Доказана теорема о сходимости к решению последовательных приближений
 |
(2.11) |
где
–
тождественный оператор; 
– оператор,
сопряженный 
Заметим, что в случае интегрального оператора (2.1)
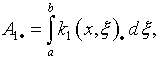
где
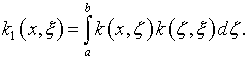
Известен целый ряд процедур убыстрения сходимости итераций по Фридману (см. [10]). Например, при условиях, которые оговорены в отношении процедуры (2.10):
 |
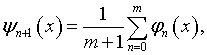(2.12) |
где
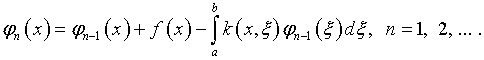
Г.М.Вайникко и А.Ю.Веретенников [19] исследовали итерационный алгоритм неявного типа:
 |
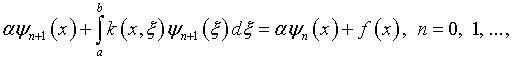(2.13) |
где
параметр
Следует подчеркнуть, что в отличие от регуляризации вида (2.6),
базирующейся на малости
для рассматриваемого подхода характерно итерирование при, напротив, достаточно
большом значении указанного параметра. Наряду с этим, к достоинствам процедур
(2.10) – (2.13)
относится возможность конструктивного использования апостериорной оценки погрешности
решения для завершения итераций.
В простейшем случае находится номер 
при
котором впервые
где
и
– погрешности
определения соответственно и 
– постоянные,
удовлетворяющие ряду требований по обеспечению устойчивости вычислительных операций.
Исследовано также влияние на сходимость последовательных приближений ошибок, малых
в вероятностном смысле.
Авторы [20] привели доводы о целесообразности сочетания регуляризации уравнения вида (2.1), параметром которой является номер итерации, с алгоритмами типа наискорейшего спуска. Такой подход восходит к публикации В.М.Фридмана [21] и реализуется, в частности, по схеме
 |
(2.14) |
где
что адекватно выбору шага спуска из условия минимума функционала невязки
Сформировавшиеся в данной области подходы отражает монография О.М.Алифанова, Е.А.Артюхина и С.В.Румянцева [20]. В процедуре математической постановки задач выделены структурная и параметрическая идентификация, подразумевающие соответственно качественное описание рассматриваемых процессов посредством дифференциальных операторов и наделение модели количественной информацией.
Использована также трактовка физических процессов в категориях причины и следствия. К причинным показателям отнесены граничные и начальные условия с их параметрами, коэффициенты дифференциальных уравнений, а также область определения задачи. Следственные показатели отражают состояние исследуемого объекта, представляя, главным образом, поля различного рода физических величин.
Восстановление причинных показателей по информации о физических полях рассматривается в качестве обратной задачи. Одним из ключевых, является соображение (с.11): «Нарушение естественной причинно-следственной связи, имеющее место в постановке обратной задачи, может привести к ее математической некорректности, чаще всего неустойчивости решения. Поэтому обратные задачи представляют собой типичный пример некорректно поставленных задач».
В привязке к искомым функциям выделены следующие типы обратных задач идентификации физических процессов для уравнений в частных производных:
1) Ретроспективные – установление предыстории некоторого состояния процесса.
2) Граничные – восстановление граничных условий или содержащихся в них параметров.
3) Коэффициентные – определение коэффициентов уравнений.
4) Геометрические – нахождение геометрических характеристик контура области или координат точек внутри нее.
Отмечено принципиальное различие между обратными задачами идентификации и управления по отношению к ширине классов возможных решений. Если в первом случае их увеличение сопряжено с осложнениями при численной реализации, то во втором, наоборот, является благоприятным фактором. Кстати, алгоритмическое обеспечение [20] почти всецело базируется на методах решения интегральных уравнений первого рода, к которым сводятся конкретно рассматриваемые задачи теплообмена.
При постановке обратных задач математической физики первостепенную значимость имеет доказательство соответствующих теорем существования и единственности решения. В этой связи можно отметить общий подход, схематично обозначенный А.Л.Бухгеймом [22, с.133-134]. Итак, рассматриваются уравнения
 |
(2.15) |
где
–
оператор прямой задачи; 
– «информационный»
оператор, описывающий закон изменения правой части; 
– заданный,
а 
и
– искомые
элементы соответствующих функциональных пространств.
Применение оператора
к первому уравнению (2.15)
дает 
что равносильно
где
– коммутатор
операторов и 
Смысл коммутирования объясняется тем, что, как правило, о функции
ничего, кроме (2.15),
неизвестно и поэтому оператор
проще изучать на решении прямой задачи 
которое удовлетворяет некоторой совокупности краевых условий. Существенно, что
в типичных приложениях оператор
не «портит» часть граничных условий, отражающую область определения
оператора 
В результате осуществляется своеобразная факторизация обратной задачи (2.15)
в произведение двух прямых задач, порождаемых операторами
и
при условии, что коммутатор им в некотором смысле «подчинен».
В тривиальном случае 
исходная
задача распадается на две более простые: 
Для
описания свойств используемых операторов привлекаются априорные оценки.
Представляют интерес выдержки из введения монографии Р.Латтеса и Ж.-Л.Лионса [23]: «В этой книге мы предлагаем метод квазиобращения, предназначенный для численного решения некоторых классов граничных задач, некорректных по Адамару. Практическая и теоретическая важность таких задач все более осознается исследователями». И далее: «Основная идея метода квазиобращения (универсальная в численном анализе!) заключается в надлежащем изменении операторов, входящих в задачу. Это изменение производится введением добавочных дифференциальных членов, которые
а) достаточно «малы» (могут быть устремлены к нулю);
б) «вырождаются на границе» (для того, чтобы, например, предупредить возникновение сложных граничных условий, а также условий, в которые могут войти неизвестные, подлежащие определению)».
В частности, некорректная постановка задачи теплопроводности
|
(2.16) |
где 
– известная
функция, заменена следующей, с малым параметром 
:
|
(2.17) |
Авторы отмечают (с.36): «При численной реализации естественно выбирать
наименее возможным, однако в задачах рассматриваемого типа следует ожидать
численную неустойчивость при 
. Поэтому можно рассчитывать только на то, что для каждой задачи существует
некоторое оптимальное значение 
равное 
». На отсутствие сходимости «в обычном смысле» решения задачи (2.17)
к точному решению, то есть при 
обратили внимание А.Н.Тихонов и В.Я.Арсенин [1,
c.52].
По мнению Ю.И.Любича, сколько-нибудь общая теория интегральных уравнений первого рода отсутствует и лишь в отдельных случаях удается использовать специальные методы. Примером является известное уравнение Абеля [24, c. 83].
Весьма показательно замечание К.И.Бабенко [25, c.310]: «Хотя с точки зрения потери информации алгоритмы и не оцениваются, нам представляется, что это важная характеристика и ее нужно учитывать». Далее, продемонстрирована неоптимальность в этом смысле целого ряда алгоритмов, включая процедуры численной реализации некорректно поставленных задач.
Глубокий анализ методологических аспектов рассматриваемой сферы представил
Р.П.Федоренко [26, пп.
40, 41]. В частности, путем минимизации функционала (2.2)
ему не удалось установить параметр регуляризации
так как при малых значениях возникали осцилляции искомой функции, а с его ростом
величина 
существенно превосходила практически допустимую. Автор пришел к выводу о том,
что причина заключается в неадекватности теории [1]
задачам управления, которые характеризуются разрывностью решений.
Исследуя задачу (2.16),
Р.П.Федоренко высказал соображение: «Все методы решения некорректных задач состоят
в том, чтобы так или иначе запретить появление в искомом ответе высоких гармоник
с большими или даже просто конечными коэффициентами. Но что такое «высокая частота»,
начиная с какого номера 
нужно считать функцию 
лишней, только портящей решение? Это, конечно, зависит от 
». Подразумевается разложение в ряд Фурье гипотетически известного решения соответствующей
прямой задачи
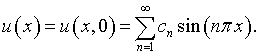
Показано, что при использованном авторами [23]
значении 
и погрешности удовлетворения в 
последнего условия (2.16)
–
порядка 
приходится ограничиваться всего лишь 
В этой связи подвергнут критике метод Р.Латтеса и Ж.-Л.Лионса, которые при решении
задачи (2.17) на сетке
с шагом 
получили совершенно неприемлемую компоненту 
а именно – 
И это при
на уровне 0,05; в условиях, когда 
Обратим также внимание на замечание [26,
с.360] о том, что кроме собственно факта ограниченности регуляризирующего оператора
(см. п.2.1), исключительно важной характеристикой является его норма 
от величины которой непосредственно зависит соотношение между точностью данной
функции 
и решением 
*
Действительно, представим уравнение (2.6) в каноническом виде
 |
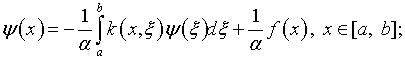(2.18) |
пусть 
и ядро
определяется выражением (1.8).
В этом случае при 
его решение [27]:
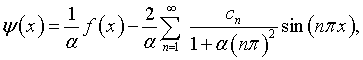
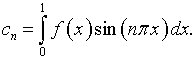
Как можно заметить, при малых значениях
погрешность представления функции
способна существенно исказить
(см. также сноску относительно уравнения (2.18)
в п.2.2).
В конструктивном плане Р.П.Федоренко рекомендует использовать традиционные постановки обратных задач дифференциального, или же вариационного характера с привлечением дополнительных условий, рационально сужающих классы возможных решений. При этом в качестве главного фактора достижения желаемой результативности указан разноплановый анализ качественных особенностей решений рассматриваемых задач, сопряженный с элементами вычислительного эксперимента.
Какие же значения параметра регуляризации
характерны для вычислительной практики? Авторы [28]
отмечают, что при решении одномерных задач восстановления зависящей от времени
плотности теплового потока на поверхности – по результатам измерений температуры
во внутренних точках тел, соответствующий диапазон весьма представителен: 10-7
– 10-4. Редакторы данной монографии придерживаются иной точки зрения:
«Можно привести много примеров решения обратных задач теплопроводности, когда
область приемлемых значений 
оказывается достаточно узкой» (с.141).
Основной аппарат численной реализации [28] трактуется его авторами как дополнение метода наименьших квадратов процедурой сглаживания осцилляций решения при высоком порядке аппроксимации. В этой связи подчеркнута родственность регуляризации по Тихонову с алгоритмами сингулярных разложений, а также гребневой регрессией (или демпфированием), которые широко применяются для подавления неустойчивости процедур метода наименьших квадратов [29].
В ряде публикаций выражена ориентация на осуществление регуляризации уравнения
(2.1) без искажений исходного
оператора по типу (2.4)
или (2.6). Так, А.П.Петров
[30] предложил постановку
задачи, в рамках которой 
посредством представления 
где 
– случайный процесс, отражающий погрешности данных и вычислений. Вместе с тем,
автору не удалось использовать формально достигаемую при этом корректность для
построения эффективного алгоритма численной реализации. Причина, по-видимому,
в недостаточности структуры
для адаптивной компенсации невязки удовлетворения (2.1).
А.В.Хованский [31]
привел доводы в плане того, что регуляризации должен подвергаться алгоритм решения
уравнения (2.1), а не оператор
(на чем базируется теория [1]).
Представляет интерес выдержка: «Более того, в тихоновской регуляризации в нерасчлененном
виде присутствуют два совершенно разных понятия: точность и устойчивость, и
происходит перекачка одного в другое. В то же время давно существует идея предобусловливания
оператора [32], хотя
лишь в контексте метода сопряженных градиентов и в мультипликативной форме».
Однако, метод сопряженных градиентов – это фактически итерации по Фридману
вида (2.14). Заметим,
что заложенная в них нелинейность способствует сглаживанию известного замедления
сходимости процедуры (2.10)
с приближением к решению уравнения (2.1).
Отмеченный эффект продемонстрировал А.Д.Мышкис [33]
с помощью представления компонентов (2.10)
рядами по собственным функциям ядра
При этом получены соотношения
где
и 
– коэффициенты
указанного разложения функций соответственно 
и 
При увеличении количества членов в представлении решения, с целью, казалось
бы, его уточнения, коэффициент сходимости 
приближается
к единице и, вследствие накопления вычислительной погрешности, итерации становятся
«контрпродуктивными».
Отметим эффективный прием подавления неустойчивости процедуры численной реализации интегрального уравнения Фредгольма второго рода
 |
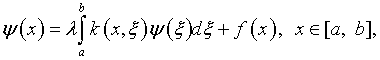(2.19) |
«расположенного на
спектре», то есть в случае, когда 
где 
– характеристическое число, предложенный П.И.Перлиным [34,
c.105-107].
Эта задача некорректна как по условию
единственности решения, так и вследствие вырожденности системы линейных алгебраических
уравнений, получаемых дискретизацией. Вместе с тем, возмущение правой части нулевым
(в пределах точности вычислений) компонентом
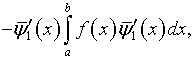
где
– нормированная
собственная функция ядра, сопряженного 
позволяет
радикально улучшить ситуацию.
Смысл в том, что теоретически решение уравнения (2.19)
разлагается в ряд по степеням 
и при согласованной с этим обстоятельством идентичности вычислительных операций
– удается компенсировать возникающую погрешность.
Исходная предпосылка А.Н.Тихонова (1943г.), позволившая рассматривать некорректно
поставленные задачи путем априорного сужения класса возможных решений, представляется
своего рода преломлением общей методологии исследования вопросов существования
и единственности в сфере численного анализа. Заметим, что 1935 г. датируется
доказательство Тихоновым известной теоремы о единственности решения обратной
задачи теплопроводности в неограниченной
-мерной области при дополнительном условии вида 
Рельефной иллюстрацией этих соображений служит алгоритм поиска квазирешения
(2.7) – (2.9).
За методом регуляризации Тихонова (1963г.) – глобальная идея предельного
перехода к точному решению по малому параметру задачи, о чем со всей определенностью
сказано в [1, c.56]:
«Отметим, что регуляризующие операторы, зависящие от параметра, использовались
в математике со времен Ньютона. Так, классическая задача приближенного вычисления
производной 
по приближенным (в метрике 
) значениям 
может решаться с помощью оператора
».
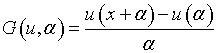Далее вместо точного значения функции подставлено
приближенное – 
где
На
основании произведенных выкладок утверждается: «Если брать 
где
при
то
при
и,
следовательно, при 
».
Следует отметить, что, используя методологию малого параметра, Тихонов получил фундаментальные результаты в области исследования дифференциальных уравнений с сингулярным возмущением вида
где
- малый параметр; 
– нелинейная функция (1948–1952 гг.).*
Решение этой системы уравнений не зависит непрерывно
от параметра 
Предельный переход
порождает объект исследования с совершенно иными свойствами. Подразумевается,
в первую очередь, проблема так называемого нарушения устойчивости корня уравнения
Тем не менее, Тихонов сумел построить весьма конструктивную теорию, на основе
которой был развит целый ряд плодотворных направлений как фундаментального,
так и прикладного характера. Значимость достижений Тихонова в сфере системного
анализа детально проанализировал Н.Н.Моисеев [36,
п.5].
Однако свойства интегрального уравнения (2.6)
при 
также радикально меняются и в этой связи, вообще говоря, возникает определенная
аналогия. Можно предположить, что Тихонов предпринял попытку использовать положения,
разработанного им аппарата теории сингулярных возмущений для решения некорректно
поставленных задач.
Это соображение подтверждает цитата из монографии С.А.Ломова [37, c.12]: «В настоящее время становится ясным, как выделять в сингулярно возмущенных дифференциальных уравнениях малые члены, которыми можно пренебречь. Оказалось, что для этого необходима дополнительная информация о решении».
Известно замечание Ж.Адамара о том, что к распространению методов теории обыкновенных дифференциальных уравнений на неодномерные задачи математической физики следует подходить с большой осторожностью [38, c.38]. Вместе с тем на рубеже 50-х гг. теория сингулярных возмущений стала эффективно использоваться при исследовании сложных задач для уравнений с частными производными (работы М.И.Вишика и Л.А.Люстерника, О.А.Олейник, К.О.Фридрихса и ряд других). Кстати, поясняя концептуальную основу своего метода квазиобращения, на перечисленных авторов, а также Тихонова ссылаются Латтес и Лионс [23, c.11].*
Одновременно они указали, что приоритетной публикации Тихонова по методу регуляризации [8] (см. также [39]) предшествовала статья Д.Л.Филлипса [40], результаты которой применительно к интегральным уравнениям аналогичны. В монографии Ф.Наттерера [41] данная регуляризация фигурирует как метод Тихонова – Филлипса. Гораздо скромнее оценил достижения последнего В.А.Морозов [6, c.10]: «Некоторые рекомендации по использованию этого метода содержатся в работах Л.В.Канторовича [42] и Д.Л.Филлипса [40]. Теоретического обоснования этого подхода в указанных работах нет».
Из хронологической справки о наиболее существенных
результатах в области построения алгоритмов решения интегральных уравнений первого
рода [10, c.234]: «1962
г. – работа Филлипса [40],
в которой предложен вариационный метод условной минимизации функционала (с использованием
ограничений на гладкость решения) и высказана идея … выбора значения параметра
регуляризации
».
Обращаясь к достижениям В.М.Фридмана, заметим, что весьма сложно судить о предпосылках, заложенных в основу итерационной процедуры (2.10). На первый взгляд, подобного типа вычислительный прием имеет множество аналогов, однако весьма неожиданной оказалась его, в определенном смысле, адекватность объекту исследования – некорректной задаче решения интегрального уравнения Фредгольма первого рода.
В дальнейшем, с целью улучшения сходимости, Фридман использовал также нелинейный алгоритм (2.14). Как представляется, различного рода способы определения номера заключительной итерации и повышения скорости сходимости (см. [14, 19, 20]), несмотря на их актуальность для практических приложений, следует рассматривать в качестве технического сопровождения методологии Фридмана.
В настоящее время алгоритмы метода сопряженных градиентов считаются одними из наиболее эффективных при решении больших плохо обусловленных разреженных систем линейных алгебраических уравнений, к которым сводится, пожалуй, большая часть задач математического моделирования [32, 43, 44]. Как указал Дж.Ортега [32], данный метод был предложен М.Р.Хестенсом и Э.Л.Штифелем (1952 г.), однако на протяжении длительного периода в силу ряда обстоятельств широко не применялся. Интерес к нему резко возрос на рубеже 70-х гг., когда удалось осознать реальную сферу приложений, потенциал упомянутого выше предобусловливания и адаптивность к распараллеливанию вычислительных операций в сочетании с архитектурой современных компьютеров.
Итак, приоритетность метода сопряженных градиентов обеспечило его преломление на класс задач линейной алгебры, характеризующихся неустойчивостью численной реализации, то есть по существу некорректно поставленных. Подчеркнем в этой связи, что «методы типа наискорейшего спуска» Фридмана [21] можно трактовать в качестве несколько упрощенных представителей семейства методов сопряженных градиентов [20, п.2.1; 43, п.7.1]. Как представляется, В.М.Фридман, первым целенаправленно применивший итерации для решения некорректно поставленной задачи, в значительной мере предвосхитил последующее развитие вычислительной математики.
В этой связи обращает внимание позиция М.А.Красносельского
и соавторов [18]. О
роли В.М.Фридмана в разработке итерационной процедуры (2.11),
являющейся аналогом (2.10),
сказано следующее: «Переход к уравнению 
указывался для некоторых случаев И.П.Натансоном [45].
Для интегральных уравнений Фредгольма второго рода он применялся еще Г.Виарда
[46]. Для интегральных
уравнений первого рода он использован по существу в работе В.М.Фридмана [17]»
(с. 73). При этом качественное различие объектов исследования осталось без комментариев.
Неординарность подхода Фридмана подчеркивает, замечание
Натансона [45]: «Для
решения интегрального уравнения первого рода наш метод неприменим. Это можно
было предвидеть заранее, потому, что в случае применения метода свободный член
в уравнении 
может быть совершенно произвольным, в то время как уравнение (2.1)
разрешимо не при всех
». Далее приведено развернутое обоснование вырожденности соответствующей дискретной
задачи.
Градиентный алгоритм Фридмана [21]
упомянут авторами [18]
исключительно в контексте уравнения 
у которого оба оператора
и
ограничены (с.115). Из резюме В.М.Фридмана к статье [21]:
«Приведено новое доказательство сходимости методов типа наискорейшего спуска
для линейного операторного уравнения и при этом не предполагается как в работах
Л.В.Канторовича [47]
и М.А.Красносельского, С.Г.Крейна [48],
что нуль есть изолированная точка спектра оператора».*
В настоящем подразделе
обозначает систему линейных алгебраических уравнений. Число обусловленности
матрицы
(см., например, [49]).
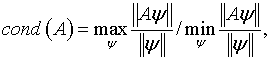
где
– множество
векторов евклидового пространства, представляет собой повышающий коэффициент между
относительной погрешностью данных и решения. Наряду с этим 
характеризует
меру близости к вырожденной
матрице, для которой решение соответствующей системы линейных алгебраических уравнений
не существует, или же не является единственным.
Алгоритм решения вырожденной системы линейных алгебраических
уравнений, базирующийся на методе наименьших квадратов, изложен в монографии
А.Н.Малышева [50]. Вначале
матрица
с помощью специального преобразования приводится к двухдиагональной и находятся
ее собственные значения, которые разбиваются на две группы: 
так, чтобы 
было не слишком велико. Затем с помощью достаточно трудоемкой процедуры «исчерпывания»
второй группы собственных значений строится матрица 
начиная с некоторого значения
устойчиво обратимая. Точность получаемого таким образом обобщенного решения
определяется по невязке 
с привлечением эвристических соображений.
Как представляется, в плане методологии данная схема напоминает алгоритм В.К.Иванова [15], который отражают расчетные соотношения (2.7) - (2.9).
Л.Хейгеман и Д.Янг [43] исследовали способ предобусловливания, используемый при решении систем линейных алгебраических уравнений, близких к вырожденным, для ускорения итераций метода сопряженных градиентов:
где
При
этом данная процедура предполагается симметризуемой в смысле существования невырожденной
матрицы 
такой,
что матрица 
является
симметричной и положительно определенной.
С помощью
исходную
задачу оказывается возможным свести к решению гораздо лучше обусловленной системы
линейных алгебраических уравнений 
где
Формально, выбор предобусловливателя не вызывает затруднений,
однако на практике приходится разрешать противоречие между условиями, которым
должна удовлетворять матрица
: «близость» к
для сокращения числа итераций; «быстрое» вычисление произведений вида 
[51]. В указанной работе
И.Е.Капорина проанализированы различные подходы к построению предобусловливателей
для систем линейных алгебраических уравнений общего вида. Аналогичная проблематика
в изложении Ортега [32]
ориентирована, главным образом, на разреженные матрицы.
Сложность задач линейной алгебры, возникающих при реализации
современных методов исследований в области механики сплошной среды, охарактеризована
следующим образом [51]:
«Матрицы соответствующих систем имеют довольно большой размер (до сотен тысяч
ненулевых элементов), достаточно сильно заполнены (до сотен и даже тысяч ненулевых
элементов в каждой строке), не имеют диагонального преобладания, не являются
-матрицами и довольно плохо обусловлены. В общем, можно рассчитывать лишь на
симметрию и положительную определенность матрицы системы».*
Заметим, что, например, в сейсмической томографии [44] приходится довольствоваться численной реализацией дискретных аналогов интегральных уравнений первого рода. Их ядра не представимы аналитически, так как параметры используемых моделей определяются с помощью натурных экспериментов.
В свете изложенного, архаичными могут показаться соображения Р.В.Хемминга [52, c.360]: «Говорят, что система линейных уравнений является плохо обусловленной, если, грубо говоря, уравнения почти линейно зависимы. Много усилий ушло на изучение того, как решать плохо обусловленные системы. Однако можно поставить вопрос: требуется ли решать такие системы в практических ситуациях? В какой физической ситуации окажутся полезными ответы, когда они так ощутимо зависят от коэффициентов системы? Обычно справедливо следующее: вместо ответа ищут систему почти линейно независимых уравнений. В свете этой информации задача может быть лучше понята и обычно переформулирована снова более удовлетворительным образом. Вполне вероятно, что плохо обусловленные системы уравнений, если исключить ошибки округления и измерения, являются действительно линейно зависимыми и, следовательно, не отражают физической ситуации».
Обратим внимание, на позициях корректности по Адамару – признанный практик. Из предисловия к [52], написанного Р.С.Гутером: «Имя Р.В.Хемминга – известного американского ученого, бывшего президента ассоциации по вычислительным машинам, руководителя математической службы «Bell Telephon Laboratories» и его работы в области вычислительной математики и теории информации достаточно хорошо известны и не нуждаются в особых рекомендациях. … Книга «Численные методы для научных работников и инженеров», бесспорно, является выдающимся явлением в математической литературе».
Весьма интересно мнение Хемминга о приоритетности вычислительных процедур [52, c.90]: «Часто думают, что главные проблемы численного анализа сосредоточены вокруг интерполяции; но это не так. К ним относятся скорее такие операции, как интегрирование, дифференцирование, нахождение нулей, максимизация и т.д. в случаях, когда все, что мы имеем или можем вычислить – это некоторые узлы функции, причем они обычно известны не точно, а приближенно, так как бывают испорчены погрешностью округления».
Итак, задача должна ставиться корректно, несмотря на неизбежные погрешности данных. Очевидно, такая позиция свидетельствует о предпочтении алгоритмической эффективности качеству исходной информации. Заметим, что упомянутая в выдержке интерполяция подразумевает приближенное представление данных задачи для проведения операций на ЭВМ с использованием конечномерной аппроксимации.
Однако в вычислительной математике распространена альтернативная концепция, отражением которой являются следующие замечания К.И.Бабенко [25]: «Для ряда областей численного анализа теория приближения является тем фундаментом, на котором покоится здание численного алгоритма» (с.138). «Вводимая в алгоритм информация характеризуется прежде всего ее объемом… . Все остальные характеристики, как, например, точность являются производными и не дают истинного представления о вводе» (с.281).
Здесь информация подразумевается
в смысле колмогоровской теории -энтропии,
отождествляющей ее с протяженностью задаваемой таблицы или алфавита, символами
которого оперирует алгоритм. Соответственно проблематика численного анализа трактуется
в категориях, образно выражаясь, издержки поиска нужных слов и стирания таблиц
при проведении операций.
Вместе с тем, близкие Хеммингу воззрения о взаимосвязи между методом исследования и используемой информацией активно развиваются группой специалистов во граве с Дж.Траубом и Г.Васильковским. Авторы [53] отмечают (сс. 9, 6): «В этой книге мы строим общую математическую теорию оптимального уменьшения неопределенности. Нас интересуют два основных вопроса: 1) Можно ли уменьшить неопределенность до заданного уровня? 2) Сколько это будет стоить? Цель теории информационной сложности – дать единый подход к исследованию оптимальных алгоритмов и их сложности для задач, в которых используется неполная, неточная или платная информация, и применить общую теорию к конкретным задачам из разных областей».
При этом под сложностью подразумевается количество арифметических операций, время их реализации, ресурсы памяти компьютера и т.п. Кстати, трактование понятия информации [52, 53] коррелирует с красноречивым высказыванием Р.Беллмана и С.Дрейфуса [54, c.342]: «К счастью, в некоторых случаях имеется очень простой способ преодоления этой трудности. Вместо того, чтобы пытаться изучать информацию как «улыбку чеширского кота», мы рассмотрим действительный физический процесс, в котором информация используется для выработки решений.* Величина информации может быть тогда измерена через эффективность решений.
Таким образом, полезность информации зависит от ее применения – это наиболее разумная концепция!»
Следует заметить, что, конечно же, и процедура конечномерной аппроксимации в задачах математической физики, на которой акцентирует внимание К.И.Бабенко, является очень важной. В самом деле, получаемая дискретная модель может оказаться некорректной, а используемые алгоритмы численной реализации расходящимися даже при решении вполне ординарных задач. Пример неустойчивой разностной схемы привели С.К.Годунов и В.С.Рябенький [55, п.4.9].
Бабенко подчеркнул также отсутствие каких-либо общих методов построения конечномерных аналогов [25, c.622]: «… обеспечение только аппроксимации недостаточно» … нужно добиться еще, чтобы дискретная задача «сохраняла тип исходной непрерывной задачи». По его мнению, для достижения указанной цели «необходимо детальное исследование в каждом конкретном случае; и это наиболее нетривиальная часть работы».
Весьма интересным представляется по существу программное заявление О.М.Белоцерковского и В.В.Щенникова в предисловии [56]:
«Бурное развитие вычислительной техники, которое особенно ярко проявилось в последние 10–15 лет, с особой остротой поставило проблему создания принципиально новой технологии решения задач на ЭВМ. … Исторически сложилось так, что проблемы численного моделирования (в это понятие мы включаем собственно математическое моделирование, сопряженное с численным экспериментом), будучи заметно продвинуты еще в «домашинный» период и развиваясь опережающими темпами в последующие периоды, оказались наиболее консервативной компонентой современной математической технологии решения задач на ЭВМ. Прибегая, может быть к излишней с точки зрения математиков образности изложения, можно охарактеризовать сложившуюся ситуацию двумя устойчивыми тенденциями:
- увеличение сложности математических моделей;
- построение очень изощренных математических методов.
И та и другая тенденция неизбежно приводят к технологическому тупику, поскольку создают практически трудно преодолимые сложности в решении задачи создания программно-аппаратных средств поддержки функционирования всей технологической цепочки … . Не претендуя на глубину и значимость аналогии, мы отваживаемся утверждать, что ситуация, складывающаяся в современном численном моделировании, схожа с ситуацией, наблюдавшейся в механике перед появлением основных идей и концепций квантовой механики».
Во вступительной статье [56] те же авторы акцентируют внимание на феномене накопления погрешностей округлений при численной реализации алгоритмов, включающих до 1012 операций, а также отсутствии реальных средств оценки погрешности решений, в частности, эволюционных задач. По их мнению: «… вполне обоснованным является следующее заключение: априори любая эволюционная задача на больших временах является численно (или вычислительно) некорректной в смысле отсутствия практически значимого решения. …
В случае же, если отсутствует априорная или апостериорная информация о погрешности приближенного решения, нельзя говорить о существовании решения. Этот вывод вполне согласуется с теоремой А.Н.Тихонова, утверждающей, что задача с данными об операторе и правой части не имеет решения во множестве приближенных чисел».
Белоцерковский и Щенников назвали конструктивной идею ассамблирования дискретных моделей рассматриваемых задач с целью повышения точности информации о решении посредством специальной суперпозиции. Предложено также искать решение в классе функций с ограниченной вариацией, что придало бы разностному оператору задачи сглаживающие свойства.
Известно сколь большое внимание уделял методологии математического моделирования Н.Н.Яненко (см. [2]). Выдвинутую им концепцию преодоления обозначенного кризиса поясняет О.М.Белоцерковский [57, c.106]:
«Исследование разностных схем, аппроксимирующих различные классы уравнений математической физики, приводит Н.Н.Яненко к расширению понятия схемы. Впервые он начинает рассматривать разностную схему как самостоятельный объект исследования, как математическую модель, адекватную той или иной физической модели. Это фундаментальное положение основано на глубоком понимании основ дифференциального и интегрального исчисления.
Действительно, физико-математические модели, описываемые дифференциальными, интегральными или интегро-дифференциальными уравнениями, получают из дискретных моделей путем осреднения и предельного перехода по тем или иным параметрам. Это имеет место, например, в модели сплошной среды, где для достаточно большого числа элементов в единице объема путем осреднения и предельного перехода по объему приходят к понятию сплошной среды. В этой связи можно трактовать разностную схему как самостоятельную математическую модель, обладающую теми или иными свойствами».
Обратим внимание на основополагающие, пожалуй, соображения Яненко [2]: «Объекты современной математики, теоретическое «ядро» которой составляют топология, геометрия, алгебра и функциональный анализ, представляют собой идеальные логические конструкции, образующие некоторую операционную систему. Мы будем называть их идеальными объектами, подчеркивая тем самым, с одной стороны, их практическую недостижимость и нереализуемость, а с другой – их прекрасные операционные качества, позволяющие совершать действия без потери информации. Идеальные объекты математики являются по своей сути инфинитными, требующими бесконечного числа операций» (с. 12).
«Развитие экспериментальной базы и инструмента исследования – ЭВМ – повысило интерес к таким конечным объектам как машинные числа, программы, конечные автоматы. В связи с этим принятое в ХХ веке определение математики как науки о бесконечном следовало бы заменить другим, более правильно отражающим ее сущность, т.е. как науки о соотношении конечного и бесконечного» (с.18).
Представляет интерес выдержка из [58, с.89]:
«Сделаем общее замечание о смысле постановки математически некорректных задач. Упомянутая выше меньшая ценность некорректно поставленных задач в старой литературе [Петровский И.Г. Лекции об уравнениях с частными производными. – М.: Физматгиз, 1961] трактовалась даже как их полная бессмысленность. Сейчас признается, что это не так. … Но конечно остается фактом значительная чувствительность некорректно поставленных задач к малым ошибкам. Непонимание этого может приводить к парадоксам».
На основании изложенного, можно сделать важный, как представляется, вывод: при построении концептуальных основ математического моделирования ведущие специалисты, по существу, руководствуются положением о неприменимости к его задачам теоремы Банаха об обратном операторе. Заметим, что Н.Данфорд и Дж.Шварц отнесли ее к трем основным принципам линейного функционального анализа, которые охарактеризовали как весьма плодотворные [59, c.61].*
Из руководства К. Морена [60, с.51]: «Эта теорема [о замкнутом графике] в последние годы приобрела репутацию самой важной теоремы функционального анализа, если этот последний рассматривать с точки зрения приложений».
Попытку обновления упомянутых фундаментальных основ, в акценте особой роли вычислительной математики, предпринял А.В.Чечкин [61], предложивший дифференциацию разделов математики на классические и неклассические. Соответственно: «арифметика, математический анализ, алгебра, геометрия, теория вероятности и др.; математическая логика, теория информации и статистика, теория нечетких множеств, теория алгоритмов и рекурсивных функций, методы вычислительной математики, теория разностных схем, теория кубатурных формул, методы решения некорректных задач и др.» (с.8). При этом в качестве критерия выбран факт наличия абсолютно полной, или же частичной информации о рассматриваемых объектах (точки, функции и т.д.).
Выдержка из аннотации раздела [61, c.78]: «Определяется и изучается новый вид отображений, являющихся обобщением классического понятия. Классические отображения осуществляют соответствие между точками множеств. При этом подразумевается, что точки известны с абсолютной точностью. Новые отображения, названные ультраотображениями, осуществляют соответствие между информациями о точках множеств. Основная конструкция ультраотображений, названная ультраоператорами, позволяет по отдельным сведениям о точке прообраза получать отдельные сведения о точке образа.
Определяется ультранепрерывность ультраоператоров, являющаяся широким обобщением понятия устойчивости методов. Выясняется, что для любого опорного оператора можно построить ультранепрерывный оператор над ним. Выделяется класс ультранепрерывных ультраоператоров, названных тихоновскими, для которых опорные операторы не являются непрерывными». И далее: «Они связаны с идеями и методами решения некорректных математических задач А.Н.Тихонова».
Возвращаясь к вопросу об адекватной дискретизации, приведем выдержку из резюме монографии А.А.Дезина [62], которая: «Посвящена описанию основных структур многомерного анализа и рассмотрению внутренним образом определяемых дискретных задач анализа и математической физики. Имеется в виду, что речь идет не просто об аппроксимации заданного континуального объекта, а о построении его аналога, отправляясь от понятий, допускающих дискретную трактовку».
Доводы о противоречии физическому смыслу дифференциальных моделей некоторых классов задач механики сплошной среды привел М.А.Зак [63]. В этой связи им разработан общий подход, всецело базирующийся на положениях теоретической механики при своеобразной интерпретации принципа наименьшего принуждения Гаусса.
Альтернативна позиция К.Трусделла, полагающего, что в целом континуальная механика деформируемого тела «по существу своему не только тоньше, красивее и величественнее, чем весьма скудный частный случай, называемый «аналитической механикой», но и гораздо лучше подходит для моделирования реальных тел» [64, c.10].
