2.5. Альтернативные воззрения
и разработки
По мнению Ю.И.Любича, сколько-нибудь
общая теория интегральных уравнений первого рода отсутствует и лишь
в отдельных случаях удается использовать специальные методы. Примером
является известное уравнение Абеля [24, c.
83].
Весьма показательно замечание
К.И.Бабенко [25, c.310]:
“Хотя с точки зрения потери информации алгоритмы и не оцениваются,
нам представляется, что это важная характеристика и ее нужно учитывать”.
Далее предметно продемонстрирована неоптимальность традиционного
подхода к численной реализации некорректно поставленных задач.
Глубокий анализ методологических
аспектов данной сферы представил Р.П.Федоренко [26, пп.40, 41].
В частности, посредством минимизации функционала (2.2) ему не удалось
установить параметр регуляризации a
, так как при малых значениях возникали осцилляции искомой функции,
а с его ростом величина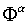 
существенно превосходила допустимую. Установлено, что причина заключается
в неадекватности теории [1] задачам управления, характеризующимся
разрывностью решений.
В контексте исследования
задачи (2.16) Р.П.Федоренко высказал соображение: “Все методы решения
некорректных задач состоят в том, чтобы так или иначе запретить
появление в искомом ответе высоких гармоник с большими или даже
просто конечными коэффициентами. Но что такое “высокая частота”,
начиная с какого номера n нужно
считать функцию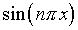 
лишней, только портящей решение? Это, конечно, зависит от T”.
Подразумевается разложение в ряд Фурье гипотетически известного
решения соответствующей прямой задачи
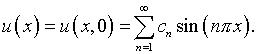
Показано, что при использованном
авторами [23] значении Т
= 0,1 и
погрешности удовлетворения в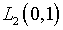 
последнего условия (2.16) – d
порядка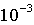 
приходится ограничиваться всего лишь n
= 2. В этой связи
подвергнут критике метод Р.Латтеса и Ж.-Л.Лионса, которые при решении
задачи (2.17) на сетке с шагом Dx
= 0,02 получили
совершенно неприемлемую компоненту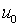 
,
а именно – 108sin(6p
x). И это при
d на уровне 0,05;
в условиях, когда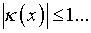 
.
Обратим также внимание на
замечание [26] о том, что кроме собственно факта ограниченности
регуляризирующего оператора G
(см. п.2.1), исключительно важной характеристикой является его норма
,
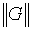от величины которой непосредственно зависит соотношение между точностью
данной функции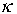 
и решения 
*
.
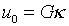| * Кстати, в большинстве профильных изданий данный момент никак
не акцентирован. |
Действительно, рассмотрим
уравнение (2.6), представленное в каноническом виде
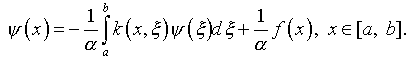(2.18)
Пусть a
= 0, b = 1
и ядро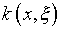 
определяется выражением (1.8). В этом случае его характеристические
числа и собственные функции соответственно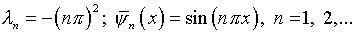 
и,
следовательно, на основании положений общей теории (см., например,
[27]) при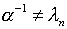 
решение уравнения (2.18)
,
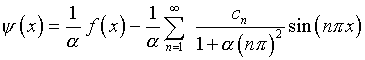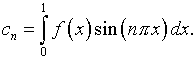
Нетрудно заметить, что при
малых значениях a погрешность определения
функции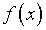 
может существенно искажать 
.
В конструктивном аспекте
Р.П.Федоренко рекомендует использовать традиционные постановки обратных
задач дифференциального, или же вариационного характера с привлечением
дополнительных условий, рационально сужающих классы возможных решений.
При этом в качестве главного фактора достижения желаемой результативности
указан разноплановый анализ качественных особенностей решений рассматриваемых
задач, сопряженный с элементами вычислительного эксперимента.
Какие же значения параметра
регуляризации a характерны для вычислительной
практики? Авторы [28] отмечают, что при решении одномерных задач
восстановления зависящей от времени плотности теплового потока на
поверхности по результатам измерений температуры во внутренних точках
тел соответствующий диапазон весьма представителен: 10-7
– 10-4.
Редакторы
упомянутого руководства придерживаются
иной точки зрения: “Можно привести много примеров решения обратных
задач теплопроводности, когда область приемлемых значений a
оказывается достаточно узкой” (с.141).
Основной аппарат численной
реализации [28] трактуется его авторами как дополнение метода наименьших
квадратов процедурой, сглаживающей осцилляции решения при высоком
порядке аппроксимации. В этой связи подчеркнута родственность регуляризации
по Тихонову с алгоритмами сингулярных разложений, а также гребневой
регрессией (или демпфированием), которые широко применяются для
подавления неустойчивости процедур метода наименьших квадратов [29].
В ряде публикаций выражена
ориентация на осуществление регуляризации уравнения (2.1) без искажений
исходного оператора по типу (2.4) или (2.6). Так, А.П.Петров [30]
предложил постановку задачи, в рамках которой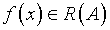 
,
посредством представления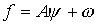 
,
где w – случайный процесс,
отражающий погрешности данных и вычислений. Вместе с тем автору
не удалось использовать формально достигаемую при этом корректность
для построения эффективного алгоритма численной реализации. Причина,
по нашему мнению, в неконструктивности структуры w
с точки зрения адаптивной компенсации невязки удовлетворения (2.1).
А.В.Хованский [31] привел
доводы в плане того, что регуляризации должен подвергаться алгоритм
решения уравнения (2.1), а не оператор А
(на чем базируется теория [1]). Представляет интерес выдержка: “Более
того, в тихоновской регуляризации в нерасчлененном виде присутствуют
два совершенно разных понятия: точность и устойчивость, и происходит
перекачка одного в другое. В то же время давно существует идея предобусловливания
оператора [32], хотя лишь в контексте метода сопряженных градиентов
и в мультипликативной форме”.
По существу подразумевается
использование уравнения (2.6) с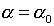 
,
где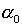 
– минимальная величина, позволяющая получать информацию об искомой
функции
косвенного характера. С ее помощью оказывается возможным определение
параметра регуляризации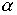 
,
согласованного с погрешностью свободного члена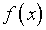 
.
Однако метод сопряженных
градиентов это фактически итерации по Фридману вида (2.14). Заметим,
что заложенная в них нелинейность способствует сглаживанию известного
замедления сходимости процедуры (2.10) с приближением к решению
уравнения (2.1). Отмеченный эффект продемонстрировал А.Д.Мышкис
[33] с помощью представления компонентов (2.10) рядами по собственным
функциям ядра .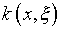
При этом получены следующие соотношения
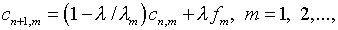
где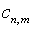 
и 
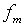– коэффициенты указанного разложения соответственно 
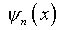и .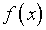
При увеличении количества
членов в представлении решения с целью, казалось бы, его уточнения,
коэффициент сходимости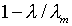 
приближается к единице и, вследствие накопления вычислительных погрешностей,
итерации становятся контрпродуктивными.
Отметим эффективный прием
подавления неустойчивости алгоритма решения интегрального уравнения
Фредгольма второго рода
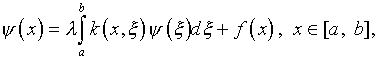(2.19)
“расположенного на спектре”,
то есть в случае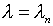 
,
разработанный П.И.Перлиным [34, c.105-
107].
Данная задача некорректна
как по условию единственности решения, так и вследствие вырожденности
системы линейных алгебраических уравнений, получаемых дискретизацией.
Вместе с тем возмущение правой части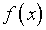
нулевым (в пределах точности вычислений) компонентом
,
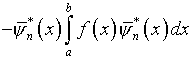где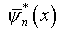 
– нормированная собственная функция ядра 
,
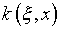позволяет радикально улучшить ситуацию.
Смысл в том, что теоретически
решение уравнения (2.19) разлагается в ряд по степеням l
и при согласованной с этим обстоятельством идентичности вычислительных
операций – удается компенсировать допускаемые погрешности.
