3.3. Методология решения некорректных задач

3.3. Методология решения некорректных задач

Некорректно поставленные задачи математической физики обманчиво прозрачны с точки зрения интерпретации рассматриваемых процессов, что обуславливается их адекватностью пространствам, которые в вычислительном отношении практически нереализуемы. Если же данные таких задач определены в естественных для них классах функций, соответствующие постановки утрачивают математический смысл, вследствие своей неразрешимости. В столь нетривиальной ситуации, конечно же, исключительно значима роль общеметодологических концепций, иначе говоря, необходимо руководствоваться какой-то системой глобальных принципов.

Исходя из этого, если утверждение Ж.Адамара о необходимости корректной постановки задач, описывающих физические явления [1], еще можно трактовать в качестве своего рода гипотезы, то по существу родственная ему теорема Банаха об обратном операторе – общепризнанный компонент фундамента современной математики [22]. Тем не менее А.Н.Тихонов избрал альтернативную направленность путем пересмотра собственно понятия о решении некорректной задачи и использования в преломлении к нему специальных алгоритмов численной реализации [2]. Как представляется, такой выбор вполне гармонировал с настроениями научной общественности последних десятилетий по поводу беспрецедентно революционной роли вычислительной математики в системе естествознания (см. [3, 23–25]).

Появилось понятие корректности по Тихонову, обыгрывающее сравнительно простой вариант поиска решения в суженном классе функций, для которого соответствующая постановка корректна [14]. Кстати, какие-либо априорные предпосылки в отношении установления такого класса на основании информации содержательного плана – отсутствуют.

Зыбкость концептуальной основы обрекла на провал идею осуществления предельного перехода по малому параметру в решении семейства задач, родственных некорректно поставленной (метод регуляризации [2]). Причина, по нашему мнению, во все той же неадекватности использования функциональных пространств. Если 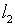характеризуется совокупностью бесконечного набора признаков, а 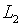– всего одним, то можно ли, даже из сугубо эвристических соображений, надеяться на преодоление столь кардинального противоречия с помощью параметра регуляризации a?

Положение, сложившееся в сфере деятельности многочисленных последователей А.Н.Тихонова, представляется весьма неприглядным. Фактически усилия сконцентрированы вокруг суррогата с малым множителем a , образованного на базе (3.1):

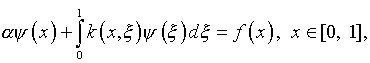(3.2)

который именуется интегральным уравнением Фредгольма второго рода, без упоминаний о его в этом смысле неполноценности. Несмотря на огромный поток исследований, посвященных определению параметра регуляризации a , сколько-нибудь конструктивные алгоритмы отсутствуют. Главная причина видится в несостоятельности тезиса, подразумевающего возможность эффективного согласования решений с данными некорректно поставленных задач (см., например, [2, 26]).

По существу приходится довольствоваться всего лишь сопоставлением решений уравнения (3.2), получаемых в диапазоне уменьшения a . В связи с высокой трудозатратностью численной реализации при малых значениях параметра регуляризации, широкомасштабное внедрение методологии А.Н.Тихонова в практику научных исследований нанесло значительный экономический ущерб. Что касается попыток исследования интегрального уравнения Фредгольма первого рода в функциональных пространствах его корректной разрешимости, то они носили единичный характер и не сопровождались конструктивным воплощением [27].

В.М.Фридман, работы [28, 29] которого рассмотрены в п.2.3, подошел к решению интегрального уравнения Фредгольма первого рода как математически поставленной задаче, безотносительно его приемлемости для моделирования конкретных процессов. С позиций настоящего изложения, итерационные алгоритмы В.М.Фридмана интересны, пожалуй, прежде всего достижением максимально возможной результативности в рамках выбранного объекта исследования, о чем косвенно свидетельствует их простота и лаконичность.

Иначе говоря, большего от уравнения (3.1) в его ординарной трактовке добиться едва ли возможно – при том, что формально сходимость существует – с приближением к решению используемые поправки становятся на фоне значений искомой функции пренебрежимо малыми:

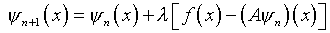Известно, что без своевременного останова такой процедуры вычислительный “шум” от операций с несоизмеримыми числами способен радикально исказить решение [5, 15]. Становится очевидным, что в силу своей природы интегральное уравнение Фредгольма первого рода содержит неустранимый дефект, принципиально не согласующийся с содержательной постановкой задачи о восстановлении функции по правой части (3.1).

Соответственно вполне естественным представляется дополнение интегрального уравнения (3.1) компонентой, которая, адаптивно компенсируя негативный фактор вычислительного “шума”, не влияла бы существенно на исходную математическую модель в силу своей малости (см. конструктивные предпосылки п.1.4).

В п.2.5 приведено соображение К.И.Бабенко [23] о необходимости учитывать фактор потери информации при оценке сравнительной эффективности вычислительных алгоритмов. Как представляется, в еще большей мере это актуально на этапе постановки задачи. Поскольку при вычислении 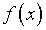по формуле (3.1) информация о функции объективно скрадывается, ее восстановление в рамках традиционного подхода вполне закономерно сводится к некорректной задаче.

Если гипотетически предположить, что искомая функция присутствует в уравнении (3.1) явно (то есть, параметр 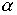уравнения (3.2) соизмерим со значениями ядра) – все обозначенные проблемы снимаются, тем не менее, любые действия по типу грубой подстановки совершенно неприемлемы. Однако подобное появление можно представить в контексте моделирования вычислительного “шума” с участием также и интегрального члена. Далее затронутый исключительно важный момент будет конкретизирован.