3.5. Соображения по развитию
конструктивной теории
Предположим, что ядро 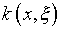 интегрального уравнения Фредгольма первого рода (3.1) замкнуто
в
интегрального уравнения Фредгольма первого рода (3.1) замкнуто
в 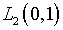 и его решение существует *.
и его решение существует *.
| * В интересах последовательности изложения,
мы повторяем некоторые из оговоренных вы-ше моментов. |
Соответственно подразумевается
возможность точного вычисления правой части посредством интегрирования,
или же принадлежность функции  пространству
пространству 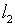 ,
означающая выполнение условия
,
означающая выполнение условия
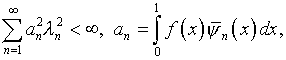 (3.3)
(3.3)
где 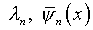 – характеристические числа и собственные функции ядра
– характеристические числа и собственные функции ядра 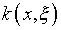 .
.
Вследствие замкнутости 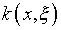 решение уравнения (3.1) также и единственно; оператор А,
отображающий из
решение уравнения (3.1) также и единственно; оператор А,
отображающий из 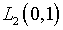 в
в 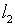 ,
непрерывен, а значит выполнены все условия теоремы Банаха об обратном
операторе. Последняя утверждает, что непрерывен и обратный оператор
А-1,
осуществляющий отображение из пространства
,
непрерывен, а значит выполнены все условия теоремы Банаха об обратном
операторе. Последняя утверждает, что непрерывен и обратный оператор
А-1,
осуществляющий отображение из пространства 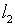 в
в 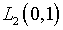 ,
иначе говоря, процедура вычисления
,
иначе говоря, процедура вычисления  устойчива к малым возмущениям данных:
устойчива к малым возмущениям данных: 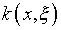 и
и  .
Соответственно ее можно реализовать без накопления погрешности округлений
значащих цифр.
.
Соответственно ее можно реализовать без накопления погрешности округлений
значащих цифр.
В этой связи Обратимый мир
С.Банаха исключительно заманчив и вместе с тем он всецело базируется
на отсутствии какой-либо дифференциации используемых пространств
по предпочтительности. Доминирующие воззрения в сфере вычислительной
математики сугубо альтернативны, из-за чего как явно, так и, преимущественно,
исподволь проводится суждение о неконструктивности упомянутой фундаментальной
теоремы.
Доводы, на первый взгляд,
резонны. В самом деле, функция  зачастую определяется с погрешностью измерений и соответственно
для ее оценки естественны пространства типа
зачастую определяется с погрешностью измерений и соответственно
для ее оценки естественны пространства типа 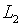 ,
ограничивающие те или иные суперпозиции значений на интервале. Пространство
,
ограничивающие те или иные суперпозиции значений на интервале. Пространство
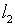 ,
как уже отмечалось выше, иллюзорно, поскольку оперирует с бесконечной
совокупностью признаков данных, становящихся в результате практически
неидентифицируемыми. Даже сравнительно малая вариация
,
как уже отмечалось выше, иллюзорно, поскольку оперирует с бесконечной
совокупностью признаков данных, становящихся в результате практически
неидентифицируемыми. Даже сравнительно малая вариация  способна нарушить критерий (3.3) и, следовательно, исказить решение
уравнения (3.1) по теореме Пикара.
способна нарушить критерий (3.3) и, следовательно, исказить решение
уравнения (3.1) по теореме Пикара.
Итак, данная фактически
функция  ,
как правило, не принадлежит пространству
,
как правило, не принадлежит пространству 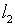 .
Исключением является тривиальный случай представления
.
Исключением является тривиальный случай представления  в виде ряда по элементам
в виде ряда по элементам 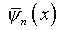 при точном определении
при точном определении 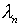 .
Однако подобные предпосылки не могут служить основанием для игнорирования
пространства
.
Однако подобные предпосылки не могут служить основанием для игнорирования
пространства 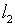 при исследовании уравнения (3.1). Как представляется, конструктивизм
здесь возможен исключительно в контексте согласования, вообще говоря,
альтернативных устремлений:
при исследовании уравнения (3.1). Как представляется, конструктивизм
здесь возможен исключительно в контексте согласования, вообще говоря,
альтернативных устремлений:
- функция

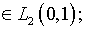
- оператор А
осуществляет отображение из
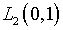 в
в 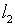 .
.
Мотивация очевидна: сохранить
потенциал непрерывной обратимости оператора А
в целях его практической реализации. Вместе с тем обозначенное противоречие
налицо и преодолеть его, ограничиваясь исключительно рамками интегрального
уравнения Фредгольма первого рода (3.1), не представляется возможным.
В такой ситуации естественно обратиться, образно выражаясь, к происхождению
данного уравнения, то есть проблематике, связанной с постановкой
задачи.
Пусть, имеется некоторый
процесс, описываемый оператором А.
Прямая задача состоит в вычислении интеграла по формуле (3.1) при
подстановке данной функции  .
Если она представлена рядом, в частности, по
.
Если она представлена рядом, в частности, по 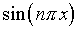 ,
соответствующие члены решения приобретают множитель
,
соответствующие члены решения приобретают множитель 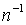 ,
вследствие чего сходимость усиливается. Указанная процедура обладает
множеством физических, а также иного характера интерпретаций и является
математически корректной.
,
вследствие чего сходимость усиливается. Указанная процедура обладает
множеством физических, а также иного характера интерпретаций и является
математически корректной.
Ключевой момент – формулировка
обратной задачи для того же оператора А,
которая сопряжена с восстановлением функции  по данной реализации процедуры интегрирования, то есть
по данной реализации процедуры интегрирования, то есть  .
Фактически подразумевается определение причины по следствию и если
схема решения прямой задачи наглядна, то ситуация в отношении обратной
– диаметрально противоположная. При ее решении приоритетной становится
собственно алгоритмическая процедура на базе адекватной математической
модели, не являющаяся аналогом процесса, проистекающего в режиме
реального времени **.
.
Фактически подразумевается определение причины по следствию и если
схема решения прямой задачи наглядна, то ситуация в отношении обратной
– диаметрально противоположная. При ее решении приоритетной становится
собственно алгоритмическая процедура на базе адекватной математической
модели, не являющаяся аналогом процесса, проистекающего в режиме
реального времени **.
| ** Действительно, порождение следствием
причины как процесс - лишено, тем более в замк-нутой системе,
физического смысла. |
В целом, традиционная постановка обратных задач
посредством формального переименования известных и неизвестных компонентов
математических моделей, описывающих объективно происходящие процессы,
– неосновательна.
Как в свете изложенного не
обратиться к утверждению Ж.Адамара о том, что все задачи, имеющие
практическое истолкование, допускают математически корректную
постановку? Исходя из этого, поскольку решение задачи, обратной
вычислению интеграла (3.1), объективно существует и единственно,
ее следует всего лишь адекватно сформулировать. Вместе с тем Ж.Адамар
не привел соответствующих рекомендаций конструктивного характера
и на современном этапе развития математической физики его методология
оказалась по существу полностью отвергнутой
***.
| *** Первая публикация Ж.Адамара по данной
проблематике относится к 1902 г. Полагают, что идея корректности
инициировала исследования С.Банаха в области теории операторов
20-х гг. |
Однако
попытаемся проследить формулировку задачи, обратной вычислению интеграла
(3.1), которое в общем случае производится с некоторой погрешностью:
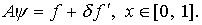 (3.4)
(3.4)
В прямой постановке ее учет
не имеет принципиального значения, тем не менее, решения интегральных
уравнений Фредгольма первого рода (3.1) и (3.4) могут быть совершенно
различными. При этом ставить вопрос о какой-либо количественной
интерпретации 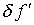 –
бессмысленно. Более того, даже в случае существования аналитического
решения
–
бессмысленно. Более того, даже в случае существования аналитического
решения 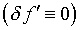 его восстановление посредством некоторой дискретизации сводится
к решению плохо обусловленной системы линейных алгебраических уравнений.
его восстановление посредством некоторой дискретизации сводится
к решению плохо обусловленной системы линейных алгебраических уравнений.
Из общих соображений, присутствие
в (3.4) 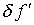 повышает потенциал постановки обратной задачи, наряду с чем возникает
принципиальный вопрос о модели допускаемой погрешности. Следует
учесть, что механизм ее генерации обуславливается фактором сглаживания
повышает потенциал постановки обратной задачи, наряду с чем возникает
принципиальный вопрос о модели допускаемой погрешности. Следует
учесть, что механизм ее генерации обуславливается фактором сглаживания
 процедурой интегрирования, а значит структура
процедурой интегрирования, а значит структура 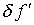 должна отражать в определенном смысле информационную несовместимость
между указанной функцией и ее отображением
должна отражать в определенном смысле информационную несовместимость
между указанной функцией и ее отображением 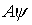 (по существу – явным и неявным представлениями).
(по существу – явным и неявным представлениями).
На основании сказанного,
воспользуемся операторной моделью погрешности вида
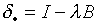 ,
(3.5)
,
(3.5)
где В
– интегральный оператор; 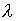 – параметр, предназначенные для адекватной аппроксимации
– параметр, предназначенные для адекватной аппроксимации 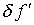 в диапазоне от нуля – до конечных искажений, связанных с измерениями.
в диапазоне от нуля – до конечных искажений, связанных с измерениями.
Таким образом, вместо интегрального
уравнения Фредгольма первого рода (3.1) предлагается решать следующую
задачу:
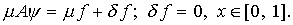 (3.6)
(3.6)
Здесь параметр 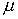 ,
как и
,
как и 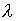 ,
предназначен для того, чтобы получаемое в результате преобразований
интегральное уравнение Фредгольма второго рода не располагалось
на спектре, что эквивалентно существованию и единственности его
решения (см., например, [34]);
,
предназначен для того, чтобы получаемое в результате преобразований
интегральное уравнение Фредгольма второго рода не располагалось
на спектре, что эквивалентно существованию и единственности его
решения (см., например, [34]); 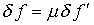 .
.
Обратим внимание, традиционная
постановка обратной задачи в виде интегрального уравнения Фредгольма
первого рода (3.1) ничем не нарушена, поскольку к его свободному
члену всего лишь прибавлена функция, представляющая нуль в 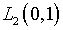 .
Вместе с тем трансформация некорректной задачи (3.1) к постановке
(3.6) создает предпосылки для кардинального изменения ситуации.
В самом деле, от
.
Вместе с тем трансформация некорректной задачи (3.1) к постановке
(3.6) создает предпосылки для кардинального изменения ситуации.
В самом деле, от 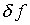 ,
вообще говоря, можно потребовать адаптивной компенсации погрешностей
вычислительных операций, выводящих
,
вообще говоря, можно потребовать адаптивной компенсации погрешностей
вычислительных операций, выводящих  из пространства
из пространства 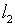 ,
вследствие чего возникают перспективы для конструктивной реализации
оператора А-1.
При
,
вследствие чего возникают перспективы для конструктивной реализации
оператора А-1.
При 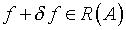 негативный фактор некорректности уравнения (3.1) в полной мере нивелируется.
негативный фактор некорректности уравнения (3.1) в полной мере нивелируется.
Как будет показано ниже,
оператор В
из (3.5), при котором 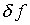 =
0 в
=
0 в 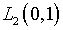 ,
целесообразно представить следующим образом:
,
целесообразно представить следующим образом:
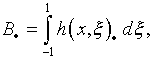
налагая на ядро 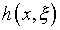 ,
преобразованное путем линейной замены переменных, условие замкнутости.
В результате задача (3.6) приобретет вид
,
преобразованное путем линейной замены переменных, условие замкнутости.
В результате задача (3.6) приобретет вид
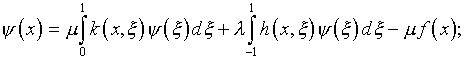 (3.7)
(3.7)
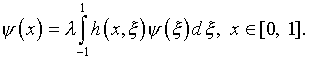 (3.8)
(3.8)
Нетрудно заметить, что условие
в отношении 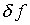 ,
эквивалентное уравнению (3.8), предполагается удовлетворить посредством
распространения
,
эквивалентное уравнению (3.8), предполагается удовлетворить посредством
распространения  на
на 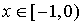 ,
равносильного использованию новой неизвестной функции.
,
равносильного использованию новой неизвестной функции.
Известно суждение будто
бы перспективы получения весомых результатов с помощью простых преобразований
математических зависимостей – невелики.
В самом деле, применив к уравнениям (3.7), (3.8) операцию вычитания,
вновь получим исходную задачу, которая некорректна. Однако, во-первых,
мы не собираемся этого делать и, во-вторых, за интегральными уравнениями
с искомой функцией в явном виде интуитивно ощутим конструктивный
потенциал.
С этой точки зрения весьма
знаменательным представляется “несрабатывание” известной демонстрации
сглаживания особенностей искомого решения процедурой интегрирования
(3.1). Действительно, предполагая, что функция 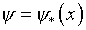 ,
удовлетворяющая системе уравнений (3.7), (3.8), известна, сообщим
ей возмущение вида
,
удовлетворяющая системе уравнений (3.7), (3.8), известна, сообщим
ей возмущение вида 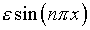 .
Подстановка в (3.6) показывает, что на свободный член
.
Подстановка в (3.6) показывает, что на свободный член 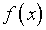 оно влияет как с понижающим коэффициентом
оно влияет как с понижающим коэффициентом 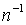 ,
так и без него – за счет соответственно интегрирования и явного
присутствия
,
так и без него – за счет соответственно интегрирования и явного
присутствия  .
.
Сказанное не распространяется
на 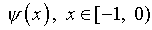 ,
однако определение данной функции выходит за рамки рассматриваемой
задачи. Подчеркнем, что последние соображения – исключительно наводящего
характера и, как будет показано, выполнение условия
,
однако определение данной функции выходит за рамки рассматриваемой
задачи. Подчеркнем, что последние соображения – исключительно наводящего
характера и, как будет показано, выполнение условия 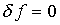 связано с рядом достаточно тонких моментов.
связано с рядом достаточно тонких моментов.
В заключение настоящего раздела
отметим неправомерность распространенного мнения о необходимости
формулировки задач математического моделирования специалистами-прикладниками
соответствующего профиля, тогда как предназначение математиков состоит
в проведении строгих аналитических исследований, разработке вычислительных
методов и участии в их реализации.
Как представляется, прикладники
должны заниматься постановкой прямых и в целом корректных задач.
Фактор некорректности непосредственно сопряжен с методом решения,
вследствие чего уделом математиков является приведение постановок
задач, интерпретирующих рассматриваемые процессы, к условиям эффективного
применения теоремы Банаха об обратном операторе.
Литература
к разделу
- Адамар Ж. Задача Коши
для линейных уравнений с частными производными гиперболического
типа. – М.: Наука, 1978. – 351 с.
- Тихонов А.Н., Арсенин
В.Я. Методы решения некорректных задач. – М.: Наука, 1979. – 285
с.
- Яненко Н.Н., Преображенский
Н.Г., Разумовский О.С. Методологические проблемы математической
физики. – Новосибирск: Наука, 1986. – 296 с.
- Морозов В.А. Регулярные
методы решения некорректно поставленных задач. – М.: Наука, 1987.
– 239 с.
- Верлань А.Ф., Сизиков
В.С. Интегральные уравнения: Методы, алгоритмы, программы. Справочное
пособие. – Киев: Наукова думка, 1986. – 543 с.
- Крейн С.Г. Линейные уравнения
в банаховом пространстве. – М.: На-ука, 1971. – 104 с.
- Пуанкаре А. О науке.
– М.: Наука, 1983. – 559 с.
- Проблемы Гильберта /Под
ред. П.С.Александрова. – М.: Наука, 1969. – С.54–55.
- Стеклов В.А. Основные
задачи математической физики. – М.: Наука, 1983. – 432 с.
- Петровский И.Г. Лекции
об уравнениях с частными производными. – М.: Физматгиз, 1961.
– 400 с.
- Пригожин И., Стенгерс
И. Порядок из хаоса: Новый диалог человека с природой. – М.: Прогресс,
1986. – 431 с.
- Курант Р., Гильберт Д.
Методы математической физики. – М.;Л.: Гостехтеориздат, 1945.
– Т.2. – 620 с.
- Банах С.С. Курс функціонального
аналізу. – Київ: Радянська школа, 1948. – 216 с.
- Лаврентьев М.М., Савельев
Л.Я. Линейные операторы и некорректные задачи. М.: Наука, 1991.
– 331 с.
- Вайникко Г.М., Веретенников
А.Ю. Итерационные процедуры в некорректных задачах. – М.: Наука,
1986. – 181 с.
- Колмогоров А.Н., Фомин
С.В. Элементы теории функций и функционального анализа. – М.:
Наука, 1989. – 623 с.
- Люстерник Л.А., Соболев
В.И. Элементы функционального анализа. – М.: Наука, 1965. – 520
с.
- Функциональный анализ
/Под ред. С.Г.Крейна. – М.: Наука, 1972. – 544 с.
- Михлин С.Г. Курс математической
физики. – М.: Наука, 1968. – 575 с.
- Михлин С.Г. Линейные
уравнения в частных производных. – М.: Высшая школа, 1977. – 431
с.
- Михлин С.Г. Некоторые
вопросы теории погрешностей. – Л.: Изд-во Ленинградск. ун-та,
1988. – 333 с.
- Данфорд Н., Шварц Дж.
Линейные операторы: Общая теория. – М.: Изд-во иностр. лит., 1962.
– 895 с.
- Бабенко К.И. Основы численного
анализа. – М.: Наука, 1986. – 744 с.
- Рациональное численное
моделирование в нелинейной механике /Под ред. О.М.Белоцерковского.
– М.: Наука, 1990. – 123 с.
- Чечкин А.В. Математическая
информатика. – М.: Наука, 1991. – 412 с.
- Бакушинский А.Б., Гончарский
А.В. Некорректные задачи. Численные методы и приложения. – М.:
Изд-во Московск. ун-та, 1989. – 198 с.
- Петров А.П. Оценки линейных
функционалов для решения некоторых обратных задач //Журнал вычислительной
математики и математической физики. – 1967. – 7. – №3. – С.648–654.
- Фридман В.М. Метод последовательных
приближений для интегрального уравнения Фредгольма 1-го рода //Успехи
математических наук. – 1956. – 11. – №1. – С.233–234.
- Фридман В.М. О сходимости
методов типа наискорейшего спуска //Успехи математических наук.
– 1962. – 17. – №3. – С.201–208.
- Ортега Дж. Введение в
параллельные и векторные методы решения линейных систем. – М.:
Мир, 1991. – 365 с.
- Хемминг Р.В. Численные
методы (для научных работников и инженеров). – М.: Наука, 1968.
– 400 с.
- Беллман Р., Дрейфус С.
Прикладные задачи динамического программирования. – М.: Наука,
1965. – 458 с.
- Николай Николаевич Яненко.
Очерки. Статьи. Воспоминания /Сост. Н.Н.Бородина. – Новосибирск:
Наука. 1988. – 303 с.
- Краснов М.Л. Интегральные
уравнения: Введение в теорию. – М.: Наука, 1975. – 303 с.

