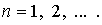4.2. Трансформированная постановка задачи
Однако для более полного использования возможностей
аппарата интегральных уравнений, из общих соображений, хотелось
бы иметь дело с представлением погрешности вида (4.6). В этой связи
введем новые неизвестные функции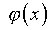 
и 
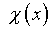следующим образом:
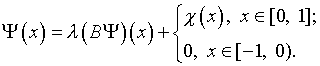(4.27)
Здесь
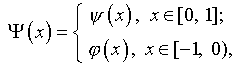
где 
– решение задачи в смысле (4.8);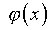
– определяется через
из интегрального уравнения Фредгольма второго рода
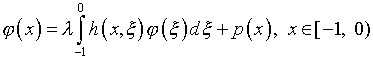
со свободным членом
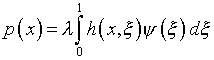
и характеристическими числами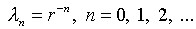 
(см.
преобразование к интегралу Пуассона п.4.1).
Иначе говоря,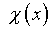
представляет комбинацию гипотетически известного решения рассматриваемой
задачи и функции ,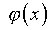
посредством которой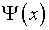 
удовлетворяет уравнению, аналогичному (4.9), но уже не в среднем,
а равномерно на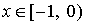 
.
При этом (4.27) – интегральное уравнение Фредгольма второго рода
относительно .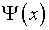
С учетом (4.1) на основе (4.27) можно представить
уравнение
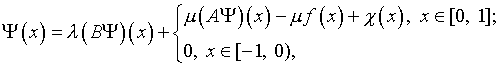(4.28)
которое в силу (4.8), строго говоря, не является
как интегральным, так и относящимся к типу Фредгольма второго рода.
Вместе с тем данное возражение легко снимается, если аналогично
(4.2) в правой части (4.28) вычесть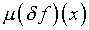 
.
При этом на основании известной устойчивости свойств
интегральных уравнений Фредгольма второго рода к малым возмущениям
[6], вполне достаточным является выполнение условия (4.7). Таким
образом, фактическое отсутствие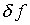 
в (4.28) не окажет существенного влияния на результаты последующих
выкладок с использованием данного уравнения.
С помощью решения интегрального уравнения Фредгольма
второго рода
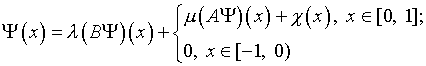(4.29)
на ,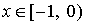
которое мы обозначим через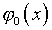 
,
функцию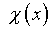
в (4.27) можно исключить.
В результате будем иметь уравнение вида
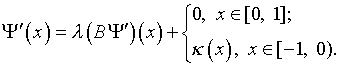(4.30)
Здесь
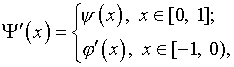(4.31)
где
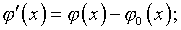
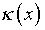– еще одна неизвестная 
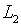-функция
*.
| * Что определяется, в частности, типом уравнений (4.27) -
(4.29). |
При этом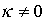 
,
так как в противном случае решение уравнения (4.30) являлось бы
тривиальным. Как можно заметить, взаимосвязь между уравнениями (4.30)
и (4.27), (4.28) реализуется посредством процедуры своеобразного
“перетекания” функции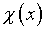 
в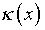
через их решения на .
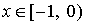Итак, от традиционной постановки (4.1) мы перешли
к интегральным уравнениям Фредгольма второго рода (4.27), (4.28)
и (4.30). В свете наших соображений общеметодологического характера
пп.1–3, за ними видится мощный потенциал конструктивной направленности.
Действительно, структура свободных членов такова,
что каждое из решений на части интервала определения (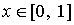
или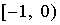 
)
содержит новые неизвестные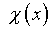
и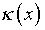
в явном виде. Одновременно в выражениях решений на оставшейся части
присутствуют исключительно интегральные члены **.
| ** Следует принять во внимание вид решения интегрального уравнения
Фредгольма второго рода посредством резольвенты (см., например,
[7]). |
Тем самым создается предпосылка аналогичного представления
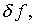что по существу является стратегической целью предлагаемого метода.
Возвращаясь к вопросам п.4.1, отметим, что на основании
(4.30) оказывается возможным непосредственное распространение уравнений
(4.5), (4.9):
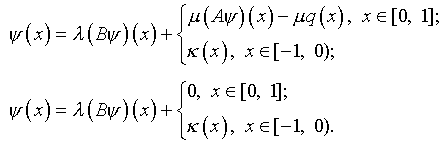(4.32)
При этом по существу
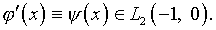
Для дальнейших преобразований понадобится обращение
оператора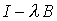 
,
или с учетом замены переменных: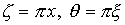 
,
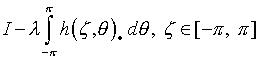(4.33)
где
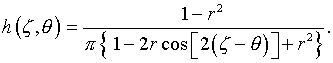
Данное ядро зависит от разности аргументов, функция
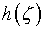обладает на 
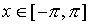периодичностью. Соответственно собственные функции и характеристические
числа оператора (4.33) суть [1]:
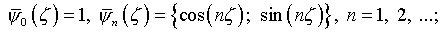
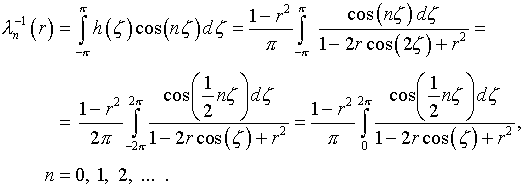
Известно [2, с.161], что
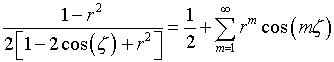
и, следовательно,
.
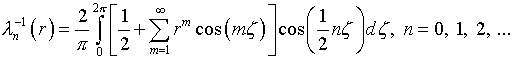В результате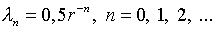 
и резольвента рассматриваемого оператора [4]
,
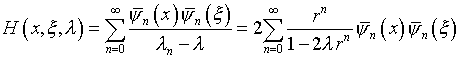(4.34)
где
,
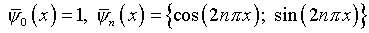