4.5. О других вариантах преобразований
Применяя к уравнениям (4.27), (4.30) операцию вычитания,
получаем интегральное уравнение Фредгольма второго рода
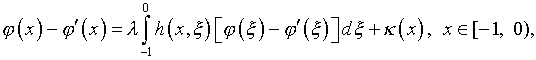
решение которого имеет вид
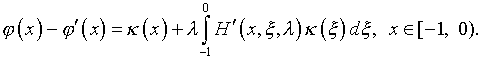(4.68)
Здесь резольвента
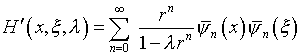(4.69)
находится по аналогии с изложенным в п.4.1.
Из уравнения (4.30)
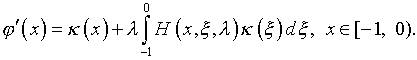(4.70)
Подстановка выражений (4.35) и (4.70) в (4.68) приводит
к интегральному уравнению Фредгольма первого рода
,
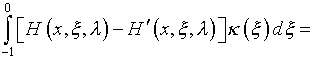
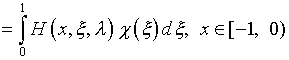(4.71)
которое, тем не менее, позволяет установить зависимость
между коэффициентами Фурье входящих функций
,
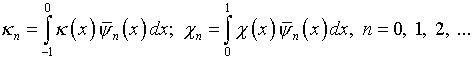что может показаться весьма заманчивым.
Однако подстановка (4.34), (4.69) в (4.71) дает
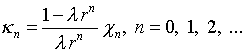
и выражение (4.42) сводится к (4.36). Соответственно
функция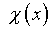 
в левой части (4.41) сокращается и безрезультативность выкладок
очевидна.
Причина заключается в том, что любые попытки представления
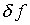с явным присутствием функции, относительно которой выстраивается
интегральное уравнение Фредгольма второго рода, вне привязки к данным
задачи (4.1), как это было сделано выше, – заведомо не имеют перспективы
*.
| * Здесь подразумевается использование уравнения (4.29). |
В (4.3) заменим оператор (4.4) на (4.25) и обратимся
к системе уравнений (4.32), где ядро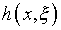 
может быть отличным от (4.14); параметр 
.
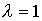Очевидно,
,
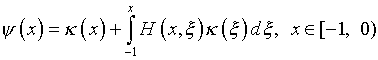где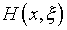 
– резольвента ядра ,
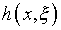и рассматриваемая задача фактически сводится к постановке (4.26)
с новой неизвестной функцией
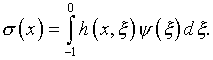
Соответствующая система интегральных уравнений приобретает
вид
.
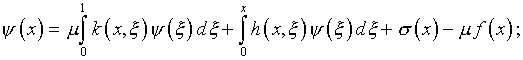
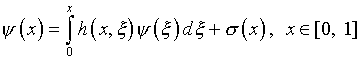(4.72)
Воспользуемся процедурой последовательных приближений
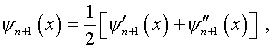
где
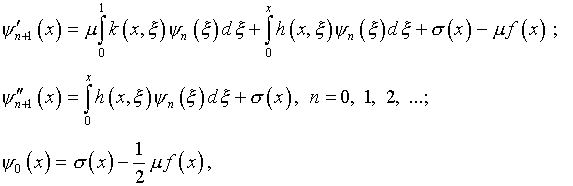
из которой
,
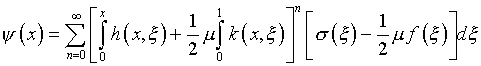(4.73)
причем значение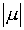 
предполагается малым настолько, что этот ряд сходится.
Подстановка выражения (4.73) в (4.72) приводит
к тому, что не только функция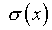 
,
но и неопределенные интегралы от нее сокращаются. Если ограничиться
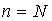числом членов ряда, слагаемое указанного типа, а именно
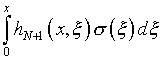
сохранится. Здесь итерированное ядро
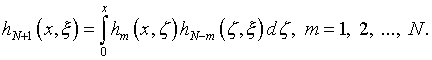
Выбирая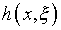
так, чтобы
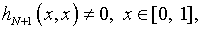
путем дифференцирования (4.73), в предположении
существования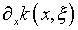 
и 
,
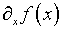можно получить интегральное уравнение Фредгольма второго рода относительно
функции .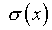
Его структура определяется раскрытием степеней суммы операторов
в (4.73) по биномиальной формуле Ньютона:
,
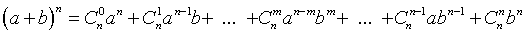(4.74)
где
.
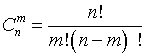Для повышения эффективности процедуры численной
реализации очевидна целесообразность максимизации множителя при
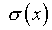в явном виде, то есть 
,
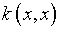что достигается, вообще говоря, за счет усиления осцилляции ядра
.
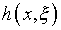Данное обстоятельство сказывается также и на возрастании интегральных
членов, однако у имеющих превалирующие коэффициенты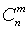 
- менее существенно. С другой стороны, сходимость ряда (4.73)
при этом объективно ухудшается.
В целом, при достаточно большом N получаемое
интегральное уравнение можно представить не содержащим малого множителя
при искомой функции ,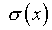
входящей явно. Вместе с тем как собственно его структура, так и
соответствующие выкладки были бы исключительно громоздки. С конструктивных
позиций намеченный подход радикально проигрывает алгоритму п.4.3.
Заметим, что интегральные члены обозначенного уравнения,
как это вытекает из (4.74), имеют вид
.
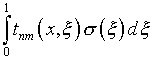(4.75)
Здесь
,
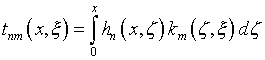(4.76)
где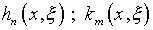 
– итерированные ядра соответствующего порядка, однако извлечь какие-либо
преимущества посредством априорной адаптации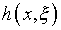
не представляется возможным.
Причина не только в сложности восстановления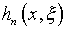 
из интегрального уравнения (4.76) – практически невозможно указать
вид несингулярного ядра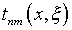 
,
при котором интеграл (4.75) допускал бы эффективное обращение (см.
[15]).
Действительно, своеобразным исключением в этом смысле
является интеграл Шлемильха [1]
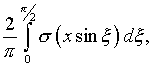
который, однако, не вписывается в предлагаемые построения.
Кратко остановимся на еще одном варианте, представив
в (4.26)
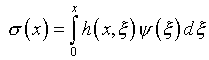
с ядром ,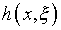
подлежащим определению.
Задача сводится к решению системы уравнений
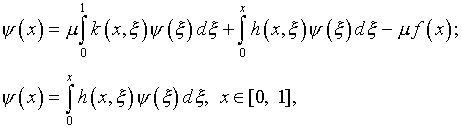(4.77)
в которой наряду с 
неизвестным является также и ядро .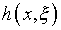
Процедура последовательных приближений, аналогичная
намеченной выше, при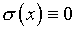 
дает решение в виде ряда (4.73). Подстановка последнего в (4.77)
приводит к уравнению с искомой функцией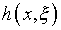
вне интеграла, иначе говоря – второго рода, однако существенным
образом нелинейному. Осложняющим решение фактором является также
и его более высокая размерность.
Модель погрешности (4.26), аналогичная использованию
в (4.3) оператора (4.25), обладает по сравнению с (4.4) большей
общностью. При этом как бы подразумевается интуитивно привлекательная
интерпретац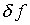ия
в равномерной метрике, однако приведенные выкладки свидетельствуют
о том, что и менее жесткое условие (4.7) оказалось для их осуществления
вполне достаточным. Соответственно представление (4.26) можно охарактеризовать
как не отражающее качественную особенность механизма сглаживания
информации процедурой интегрирования.
Тем не менее перспективы сведения рассматриваемой
задачи к интегральному уравнению Фредгольма второго рода на основе
(4.26) в принципе просматриваются. Из общих соображений данное обстоятельство
можно назвать примечательным.
Литература к разделу
- Краснов М.Л., Киселев А.И., Макаренко Г.И. Интегральные
уравнения. – М.: Наука, 1976. – 215 с.
- Гурса Э. Курс математического анализа. – М.;Л.:
Гостехтеориздат, 1934. – Т.3. – Ч.1. – 276 с.
- Гурса Э. Курс математического анализа. – М.;Л.:
Гостехтеориздат, 1934. – Т.3. – Ч.2. – 320 с.
- Трикоми Ф. Интегральные уравнения. – М.: Изд-во
иностр. лит., 1960. – 299 с.
- Эдвардс Р. Ряды Фурье в современном изложении.
– М.: Мир, 1985. – Т.1. – 260 с.
- Крейн С.Г. Линейные уравнения в банаховом пространстве.
– М.: На-ука, 1971. – 104 с.
- Краснов М.Л. Интегральные уравнения: Введение
в теорию. – М.: Наука, 1975. – 303 с.
- Михлин С.Г. Некоторые вопросы теории погрешностей.
– Л.: Изд-во Ленигр. ун-та, 1988. – 333 с.
- Михлин С.Г. Лекции по линейным интегральным уравнениям.
– М.: Физматгиз, 1959. – 232 с.
- Иванов В.В. Методы вычислений на ЭВМ: Справочное
пособие. – Киев: Наукова думка, 1986. – 583 с.
- Лучка А.Ю. Проекционно-итеративные методы решения
дифференциальных и интегральных уравнений. – Киев: Наукова думка,
1980. – 262 с.
- Головач Г.П., Калайда О.Ф. Наближені методи розв’язування
операторних рівнянь. – Київ: Вища школа, 1974. – 248 с.
- Васильев Н.И., Клоков Ю.А., Шкерстена А.Я. Применение
полиномов Чебышева в численном анализе. – Рига: Зинатне, 1984.
– 240 с.
- Приближенное решение операторных уравнений /М.А.Красносельский,
Г.М.Вайникко, П.П.Забрейко и др. – М.: Наука, 1969. – 455 с.
- Schmeidler W. Integralgleichungen mit anwendungen
in Phusik und Technik. – Leipzig: Akad. Verlagsgesselschaft, 1955.
– 611 s.
