| |
1.4. Предпосылки
реализации условий корректности
Предположим, что 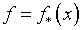 – результат точного интегрирования функции
– результат точного интегрирования функции 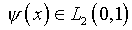 и симметричного замкнутого ядра
и симметричного замкнутого ядра 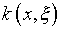 по формуле (1.6). В этом случае
по формуле (1.6). В этом случае 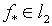 ,
причем соответствующее множество, что существенно, не является компактным.
Данное обстоятельство порождает ограниченность оператора А-1
из l2 в ,
причем соответствующее множество, что существенно, не является компактным.
Данное обстоятельство порождает ограниченность оператора А-1
из l2 в 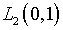 ,
определяющего решение уравнения ,
определяющего решение уравнения
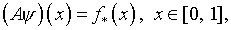 (1.11)
(1.11)
о чем упоминалось выше. Едва ли следует пояснять
сколь благоприятна в принципе подобная ситуация, при которой автоматически
удовлетворяется третье условие корректности по Адамару, к тому же
непосредственно вытекающее из существования и единственности решения.
Суть в устойчивости по определению обратной процедуры
восстановления  к малым в известном смысле возмущениям данных задачи. Соответственно
решение уравнения (1.11) может быть получено по формуле (1.10) и
при этом погрешности вычисления коэффициентов an,
следуя (1.7) с
к малым в известном смысле возмущениям данных задачи. Соответственно
решение уравнения (1.11) может быть получено по формуле (1.10) и
при этом погрешности вычисления коэффициентов an,
следуя (1.7) с 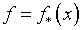 ,
а также значений ,
а также значений 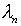 должны адекватно сказываться на
должны адекватно сказываться на  в
в 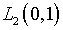 . .
Однако на самом деле коэффициенты an
находятся с погрешностью, эквивалентной 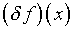 – неточности, заложенной в определение свободного члена (1.6). Иначе
говоря, правая часть уравнения (1.11) реально следующая:
– неточности, заложенной в определение свободного члена (1.6). Иначе
говоря, правая часть уравнения (1.11) реально следующая:
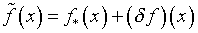 .
(1.12) .
(1.12)
При этом необходимое условие корректности уравнения
(1.11), а именно 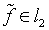 оказывается
иллюзорным, поскольку получение какой-либо количественной информации
в отношении оказывается
иллюзорным, поскольку получение какой-либо количественной информации
в отношении 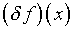 не представляется возможным.
не представляется возможным.
Заметим, что своеобразная “размытость” пространства
l2 обуславливается структурой нормирующего функционала
(1.7) в виде бесконечного ряда членов, определяемых на основании
спектральных характеристик ядра 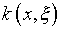 .
В этом смысле такое пространство как .
В этом смысле такое пространство как 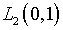 является
для функции является
для функции 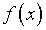 гораздо более наглядным, однако его использование влечет весьма
негативные последствия.
гораздо более наглядным, однако его использование влечет весьма
негативные последствия.
Действительно, в таком случае 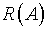 не принадлежит замкнутому подпространству
не принадлежит замкнутому подпространству 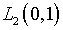 ,
операторы А и А-1 становятся соответственно
вполне непрерывным и неограниченным, вследствие чего исследование,
а также численная реализация исходного уравнения (1.6) фактически
выводятся из сферы применения фундаментальной теоремы С.Банаха об
обратном операторе. Не слишком ли дорогая расплата за в целом эфемерную,
как представляется, наглядность при постановке задачи? ,
операторы А и А-1 становятся соответственно
вполне непрерывным и неограниченным, вследствие чего исследование,
а также численная реализация исходного уравнения (1.6) фактически
выводятся из сферы применения фундаментальной теоремы С.Банаха об
обратном операторе. Не слишком ли дорогая расплата за в целом эфемерную,
как представляется, наглядность при постановке задачи?
Обратим внимание на известную точку зрения о необходимости
выбора пространств принадлежности решений задач математической физики,
исходя из практических приложений, с которой трудно не согласиться.
Вместе с тем достаточно спорным представляется также распространенное
мнение будто бы социолог, например, должен ставить задачу, решаемую
затем математическими методами, с указанием, в частности, пространств
принадлежности ее данных. Последнее, как правило, допускает вариативность,
создающую предпосылки повышения эффективности процедур численной
реализации.
Имеются ли перспективы преодоления отмеченной выше
сложности сопряжения свободного члена интегрального уравнения Фредгольма
первого рода (1.6) с адекватным ему пространством l2?
В этой связи обратимся к уравнению (1.11), которое с учетом (1.12)
приобретает вид
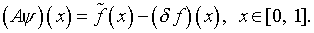 (1.13)
(1.13)
Как представляется, есть шанс приведения данной
функции 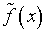 к
к 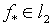 посредством адаптивного моделирования погрешности
посредством адаптивного моделирования погрешности 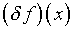 .
Действительно, .
Действительно, 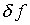 ,
а по существу сглаживание информации процедурой интегрирования,
естественно отразить разностью между искомой функцией ,
а по существу сглаживание информации процедурой интегрирования,
естественно отразить разностью между искомой функцией  в явном виде и интегралом от нее, ядро которого не налагало бы на
постановку рассматриваемой задачи дополнительных ограничений *
.
в явном виде и интегралом от нее, ядро которого не налагало бы на
постановку рассматриваемой задачи дополнительных ограничений *
.
| * Реализация обозначенной направленности - ключевой аспект
конструктивной части настоящего изложения (см. п.4). |
В развитие аналогичных соображений возникает условие
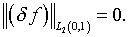 (1.14)
(1.14)
Итак, вместо традиционного восстановления функции
 посредством решения интегрального уравнения Фредгольма первого рода
(1.6) предлагается использовать, на первый взгляд, несущественное
возмущение (нуль в L2), адекватное задаче (1.13),
(1.14). Как будет показано ниже, в результате сравнительно несложных
преобразований определение
посредством решения интегрального уравнения Фредгольма первого рода
(1.6) предлагается использовать, на первый взгляд, несущественное
возмущение (нуль в L2), адекватное задаче (1.13),
(1.14). Как будет показано ниже, в результате сравнительно несложных
преобразований определение  удается свести к решению интегрального уравнения Фредгольма второго
рода, являющегося исключительно привлекательным с точки зрения эффективности
процедур численной реализации.
удается свести к решению интегрального уравнения Фредгольма второго
рода, являющегося исключительно привлекательным с точки зрения эффективности
процедур численной реализации.
В заключение заметим, что известные методы решения
уравнений вида (1.6) широко используются при кардинальном несоответствии
между 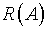 в
в 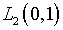 ,
или же ином пространстве и функциями ,
или же ином пространстве и функциями 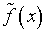 ,
которые находятся с помощью измерений. С этой точки зрения выполнение
условия (1.14) едва ли может трактоваться непосредственно и, тем
не менее, обозначенный подход остается в силе, интерпретируя, образно
выражаясь, приближение рассматриваемой задачи к поставленной корректно.
Так, сходимость ряда (1.7) должна подразумеваться с учетом соответствующей
вариации ядра ,
которые находятся с помощью измерений. С этой точки зрения выполнение
условия (1.14) едва ли может трактоваться непосредственно и, тем
не менее, обозначенный подход остается в силе, интерпретируя, образно
выражаясь, приближение рассматриваемой задачи к поставленной корректно.
Так, сходимость ряда (1.7) должна подразумеваться с учетом соответствующей
вариации ядра 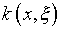 ,
что же касается алгоритмов решения получаемых в конечном итоге интегральных
уравнений Фредгольма второго рода, то на их устойчивость погрешности
измерений ,
что же касается алгоритмов решения получаемых в конечном итоге интегральных
уравнений Фредгольма второго рода, то на их устойчивость погрешности
измерений 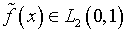 практически не влияют (см., например, [19]).
практически не влияют (см., например, [19]).
Литература к разделу
- Адамар Ж. Задача Коши
для линейных уравнений с частными производными гиперболического
типа. – М.: Наука, 1978. – 351 с.
- Волевич Л.Р., Гиндикин
С.Г. Задача Коши //Современные проблемы математики: Фундаментальные
направления. – М.: ВИНИТИ, 1985. – Т.32. – С.5–98.
- Арсенин В.Я., Тихонов
А.Н. Некорректные задачи /Математическая энциклопедия. – М.: Советская
энциклопедия, 1982. – Т.3. – С.930–935.
- Шилов Г.Е. Жак Адамар и
формирование функционального анализа: Выступление на мемориальном
заседании Московского математического общества 10 марта 1964
г. //Успехи математических
наук. – 1964. – 19. – №3. – С.183–185.
- Полищук Е.М., Шапошникова
Т.О. Жак Адамар. – Л.: Наука, 1990. – 254 с.
- Верлань А.Ф., Сизиков
В.С. Интегральные уравнения: Методы, алгоритмы, программы. Справочное
пособие. – Киев: Наукова думка, 1986. – 543 с.
- Морозов В.А. Методы регуляризации
неустойчивых задач. – М.: Изд-во Московск. ун-та, 1987. – 217
с.
- Яненко Н.Н., Преображенский
Н.Г., Разумовский О.С. Методологические проблемы математической
физики. – Новосибирск: Наука, 1986. – 296 с.
- Пуанкаре А. О науке. –
М.: Наука, 1983. – 560 с.
- Пригожин И., Стенгерс
И. Порядок из хаоса: Новый диалог человека с природой. – М.: Прогресс,
1986. – 431 с.
- Проблемы Гильберта /Под
ред. П.С.Александрова. – М.: Наука. 1969 – 239 с.
- Курант Р., Гильберт Д.
Методы математической физики. – М., Л.: Гостехтеориздат, 1945.
– Т.2. – 620 с.
- Стеклов В.А. Основные
задачи математической физики. – М.: Наука, 1983. – 432 с.
- Петровский И.Г. Лекции
об уравнениях с частными производными. – М.: Физматгиз, 1961.
– 400 с.
- Соболев С.Л. Уравнения
математической физики. – М.: Наука, 1966. – 443 с.
- Владимиров В.С. Уравнения
математической физики. – М.: Наука, 1967. – 436 с.
- Новожилов В.В. Вопросы
механики сплошной среды. – Л.: Судостроение, 1989. – 397 с.
- Краснов М.Л., Киселев
А.И., Макаренко Г.И. Интегральные уравнения. – М.: Наука, 1976.
– 215 с.
- Крейн С.Г. Линейные уравнения
в банаховом пространстве. – М.: Наука, 1971. – 104 с.
- Банах С.С. Курс функціонального
аналізу. – Київ: Радянська школа, 1948. – 216 с.
- Колмогоров А.Н., Фомин
С.В. Элементы теории функций и функционального анализа. – М.:
Наука, 1989. – 623 с.
- Люстерник Л.А., Соболев
В.И. Элементы функционального анализа. – М.: Наука, 1965. – 520
с.
- Функциональный анализ
/Под ред. С.Г.Крейна. – М.: Наука, 1972. – 544 с.
- Канторович Л.В., Акилов
Г.П. Функциональный анализ. – М.: Наука, 1977. – 742 с.
- Михлин С.Г. Курс математической
физики. – М.: Наука, 1968. – 575 с.
- Михлин С.Г. Линейные уравнения
в частных производных. – М.: Высшая школа, 1977. – 431 с.
- Михлин С.Г. Некоторые
вопросы теории погрешностей. – Л.: Изд-во Ленинградск. ун-та,
1988. – 333 с.
- Лаврентьев М.М., Савельев
Л.Я. Линейные операторы и некорректные задачи. – М.: Наука, 1991.
– 331 с.
- Вайникко Г.М., Веретенников
А.Ю. Итерационные процедуры в некорректных задачах. – М.: Наука,
1986. – 181 с.
- Бабенко К.И. Основы численного
анализа. – М.: Наука, 1986. – 744 с.
- Рихтмайер Р. Принципы
современной математической физики. – М.: Мир, 1982. – Т.1. – 486
с.
- Треногин В.А. Функциональный
анализ. – М.: Наука, 1980. – 495 с.
|

