
 |
|
|
|
|
Подытожим основные моменты изложенного выше материала. Итак, решение интегрального уравнения Фредгольма первого рода
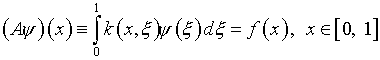 (1)
(1)
в «удобном» для реализации вычислительных
методов пространстве ![]() представляет собой некорректно поставленную
задачу. Ситуация с пространством
представляет собой некорректно поставленную
задачу. Ситуация с пространством ![]() адекватном области значений
оператора
адекватном области значений
оператора ![]() является иной: данные уравнения (1) теоретически
могут удовлетворять условиям его корректности и, тем не менее, решение будет
представлять ряд, расходящийся из-за накопления погрешности вычислений.
является иной: данные уравнения (1) теоретически
могут удовлетворять условиям его корректности и, тем не менее, решение будет
представлять ряд, расходящийся из-за накопления погрешности вычислений.
Следует принять во внимание,
что даже проверка принадлежности данных (1) пространству ![]() в общем случае практически
нереализуема. Наряду с этим, в качестве объективного фактора некорректности
выступает погрешность экпериментального определения
в общем случае практически
нереализуема. Наряду с этим, в качестве объективного фактора некорректности
выступает погрешность экпериментального определения ![]() а иногда и неточность представлений
о функции
а иногда и неточность представлений
о функции ![]() характеризующей рассматриваемую систему.
характеризующей рассматриваемую систему.
Основу работы составляет
предложение об адаптивной привязке уравнения (1) к пространству ![]() посредством моделирования
погрешности
посредством моделирования
погрешности ![]() возникающей вследствие сглаживания информации
процедурой интегрирования. При этом предполагается, что удовлетворяющая ему
функция существует, единственна и использовано условие
возникающей вследствие сглаживания информации
процедурой интегрирования. При этом предполагается, что удовлетворяющая ему
функция существует, единственна и использовано условие
![]() (2)
(2)
отражающее объективную малость этой погрешности по сравнению с ![]() и данными задачи.
и данными задачи.
Вначале из эвристических соображений, а затем и более основательно аргументирована целесообразность представления погрешности разностью искомой функции в явном виде и интегральной компоненты:
![]()
![]() (3)
(3)
где
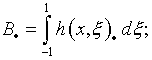
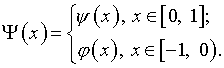
Исключительную значимость для всего комплекса выкладок, особенно в первом варианте их реализации, имело представление
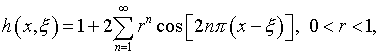 (4)
(4)
то есть, в виде ядра Пуассона, позволившее удовлетворить условие (2) для случая,
когда функция ![]() является гармонической. С использованием (2),
(3) постановка задачи (1) подверглась трансформации:
является гармонической. С использованием (2),
(3) постановка задачи (1) подверглась трансформации:
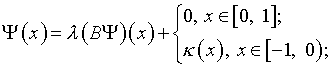 (5)
(5)
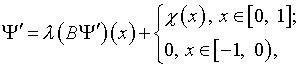 (6)
(6)
где
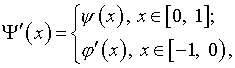
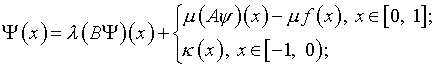 (7)
(7)
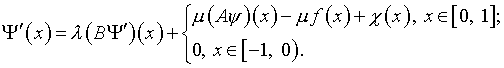 (8)
(8)
С точки зрения конструктивизма последующих выкладок, на базе (2) – (4), ключевую роль сыграли следующие факторы:
-
распространение уравнения (3)
при условии (2) на ![]() в результате чего появилось интегральное уравнение
Фредгольма второго рода (5) с неопределенной функцией
в результате чего появилось интегральное уравнение
Фредгольма второго рода (5) с неопределенной функцией ![]() – компонентой его свободного члена;
– компонентой его свободного члена;
- использование уравнения аналогичной структуры – (6), свободный член которого обращается в нуль на другой части интервала определения;
-
не вполне непрерывное возмущение
оператора ![]() путем поочередного сложения (5) и (6) с (1),
в результате чего образовались уравнения (7) и (8).
путем поочередного сложения (5) и (6) с (1),
в результате чего образовались уравнения (7) и (8).
Исключение функции ![]() из (8) с помощью уравнения
из (8) с помощью уравнения
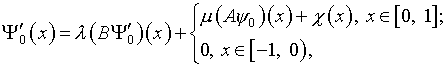 (9)
(9)
где
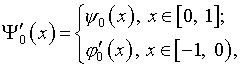
позволило получить:
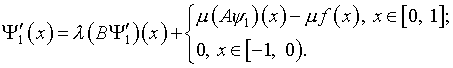 (10)
(10)
Здесь
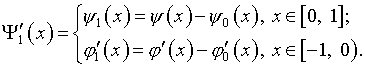 (11)
(11)
Обращение в (10) оператора
![]() привело к интегральному уравнению Фредгольма
второго рода
привело к интегральному уравнению Фредгольма
второго рода
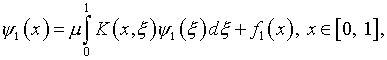 (12)
(12)
в котором ядро и свободный член определяются
данными (1); параметр ![]() как и в аналогичных случаях
как и в аналогичных случаях ![]() должен удовлетворять условию разрешимости.
После нахождения
должен удовлетворять условию разрешимости.
После нахождения ![]() функция
функция ![]() выражается в квадратурах.
выражается в квадратурах.
Из (5) и (6) следует, что
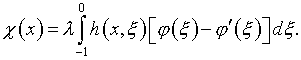 (13)
(13)
Дальнейшей направленностью
выкладок явилось определение разности функций в правой части этого выражения
так, чтобы оно превратилось в интегральное уравнение Фредгольма второго рода
относительно ![]() Неочевидность получения такого результата
сопряжена с тем, что если функция
Неочевидность получения такого результата
сопряжена с тем, что если функция ![]() просто выражается через
просто выражается через
![]() (из уравнения (6)), то в отношении
(из уравнения (6)), то в отношении ![]() аналогичная возможность отсутствует.
аналогичная возможность отсутствует.
В процессе достижения
поставленной цели, акцент был сделан на получение соотношений между решениями
(7) и (8), позволяющих превращаться одному из этих уравнений в другое. В пользу
осуществимости таких превращений свидетельствует вид свободных членов уравнений
(7), (8). Иначе говоря, возможность «перетекания» их ненулевых компонентов с
одной части интервала определения на другую, открывающая перспективу представления
![]() двумя способами – с функцией
двумя способами – с функцией ![]() входящей и не входящей в явном виде.
входящей и не входящей в явном виде.
Практическая реализация
приведенных соображений показала, что решения уравнений (5) – (8) на ![]() взаимосвязаны между собой
через функции, входящие в (9):
взаимосвязаны между собой
через функции, входящие в (9):
![]() (14)
(14)
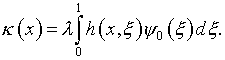 (15)
(15)
Из (11), (14)
![]() (16)
(16)
и после подстановки в (13) задача свелась к решению интегрального уравнения Фредгольма второго рода
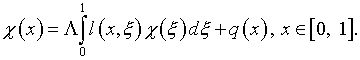 (17)
(17)
Здесь ![]()
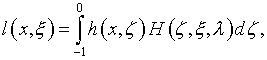
где ![]() – резольвента ядра
– резольвента ядра ![]() на
на ![]()
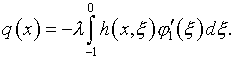
Решение уравнения (17) имеет вид
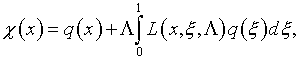
где
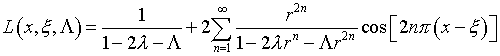
– резольвента ядра ![]()
Обращение оператора ![]() в уравнении (5) позволило
представить функцию
в уравнении (5) позволило
представить функцию ![]() рядом Фурье по элементам
рядом Фурье по элементам ![]() коэффициенты которого выражаются через данные
(1) и зависят от параметра
коэффициенты которого выражаются через данные
(1) и зависят от параметра ![]() Заметим, что на предыдущем этапе
вычислений из уравнения (12) в аналогичном виде определяется функция
Заметим, что на предыдущем этапе
вычислений из уравнения (12) в аналогичном виде определяется функция ![]()
Получаемое таким образом
решение ограничивается лишь случаем, когда функция ![]() удовлетворяющая уравнению (1), является
гармонической. Однако предельный переход
удовлетворяющая уравнению (1), является
гармонической. Однако предельный переход ![]() легко снимает проблемы,
переводя свободный член уравнения (1), а также и удовлетворяющую ему функцию
легко снимает проблемы,
переводя свободный член уравнения (1), а также и удовлетворяющую ему функцию
![]() в пространство
в пространство ![]()
И это главный момент, состоящий в достижении конечной цели преобразований. Соответственно условие (2) приобретает вид
![]()
В целом, выкладки представляются
достаточно прозрачными. Итак, определение гармонической функциии ![]() трансформировано в задачу (5) – (8). Найдена
функция
трансформировано в задачу (5) – (8). Найдена
функция ![]() – часть решения уравнения (8), зависящая
от
– часть решения уравнения (8), зависящая
от ![]() Из (14) и (11) функция
Из (14) и (11) функция ![]() определена двумя способами, что отражает
соотношение (16). Тем самым (13) превращается в уравнение (17). Наконец, в полученном
решении осуществлен переход к пределу по параметру
определена двумя способами, что отражает
соотношение (16). Тем самым (13) превращается в уравнение (17). Наконец, в полученном
решении осуществлен переход к пределу по параметру ![]()
Возможна следующая интерпретация
алгоритма преобразований. Вначале трансформированная постановка задачи «деформируется»
путем исключения функции ![]() из уравнения (8). Затем эта «деформация»
адаптивно сглаживается посредством, что очень важно, решения интегральных уравнений
Фредгольма второго рода (12), (17) и (6).
из уравнения (8). Затем эта «деформация»
адаптивно сглаживается посредством, что очень важно, решения интегральных уравнений
Фредгольма второго рода (12), (17) и (6).
Оговорен первый вариант
решения задачи. Второй вариант ее решения также базируется на соотношениях,
которые приведены выше. С использованием (15), получен аналог уравнения (17)
относительно функции ![]() решение которого имеет вид:
решение которого имеет вид:
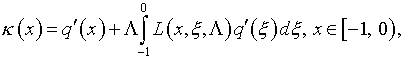 (18)
(18)
где
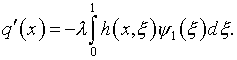 (19)
(19)
Задача (1) свелась к численной реализации, последовательно, двух интегральных уравнений Фредгольма второго рода: (12) и
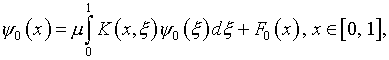 (20)
(20)
где
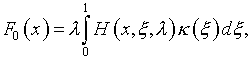
в результате чего ее решение находится как
![]()
см. также (9).
Заметим, ядра этих уравнений
– одинаковы. Показано также, что с использованием (5), (11), (18) и (19) задача
сводится к численной реализации одного интегрального уравнения Фредгольма второго
рода относительно искомой функции ![]()
В отличие от предыдущего
варианта решения, здесь не приходится вычислять коэффициенты Фурье функций ![]() и
и ![]() а также суммировать бесконечные
числовые ряды, что можно считать преимуществом. Наряду с этим, для решения уравнений
(12) и (20) имеются универсальные алгоритмы. В целом, второй вариант решения
задачи – более формализован. К достоинствам первого варианта следует отнести
возможность получения функции
а также суммировать бесконечные
числовые ряды, что можно считать преимуществом. Наряду с этим, для решения уравнений
(12) и (20) имеются универсальные алгоритмы. В целом, второй вариант решения
задачи – более формализован. К достоинствам первого варианта следует отнести
возможность получения функции ![]() в удобном, зачастую, виде
ряда Фурье.
в удобном, зачастую, виде
ряда Фурье.
Варианты решения принципиально отличаются между собой по способам удовлетворения (2), или же уравнения
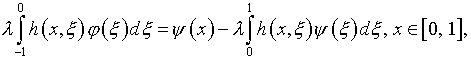 (21)
(21)
в котором при ![]() функция
функция ![]() может быть только обобщенной. Если в первом
варианте из-за этого выкладки производились с функцией
может быть только обобщенной. Если в первом
варианте из-за этого выкладки производились с функцией ![]() которая предполагалась гармонической, вплоть
до их завершающего этапа, то во втором – удовлетворение уравнения (21) подразумевается
в смысле обобщенных функций.
которая предполагалась гармонической, вплоть
до их завершающего этапа, то во втором – удовлетворение уравнения (21) подразумевается
в смысле обобщенных функций.
Конкретно, использовалось уравнение, полученное воздействием на (21) оператора
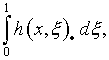
относительно обобщенных функций*
| *
Характерный момент заключается в том, что конечный результат преобразований
– такой же как, если бы не осуществляя их, постулировать возможность применения
теории интегральных уравнений Фредгольма второго рода в случае, когда функция
|
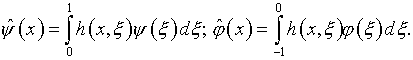
Вместе с тем, собственно
условие (2), является для реализации как первого, так и второго вариантов решения
задачи – совершенно необходимым. Действительно, уравнение (21), которое можно
назвать «внештатным», кардинально изменяет задачу (1) в постановке разрешения
интегрального уравнения Фредгольма первого рода. С помощью (2), по существу,
снимается внутренне непреодолимая проблема объективной несогласованности ![]() и
и ![]() служащая причиной некорректности
задачи (1).
служащая причиной некорректности
задачи (1).
Освобождение ![]() от формальной привязки
к
от формальной привязки
к ![]() посредством (2) и (7), (8), одновременно приводит
к тому, что свободный член уравнения (21), при рассмотрении его как
посредством (2) и (7), (8), одновременно приводит
к тому, что свободный член уравнения (21), при рассмотрении его как
![]()
где
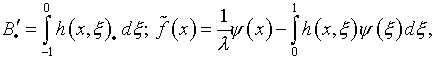
становится функциональным.
В результате, условие
![]() (которое фактически –
невыполнимо) заменяется следующим:
(которое фактически –
невыполнимо) заменяется следующим:
![]() (22)
(22)
что, на самом деле, эквивалентно
![]()
и таким образом от численного сопоставления ![]() с
с ![]() оказывается возможным перейти
к вопросу о, всего лишь, существовании функции
оказывается возможным перейти
к вопросу о, всего лишь, существовании функции ![]() позволяющей выполнить условие
(22).
позволяющей выполнить условие
(22).
Более того, поскольку
(21) представляет собой интегральное уравнение Фредгольма второго рода относительно
![]() в ходе последующих выкладок происходит как
бы перадресация статуса между
в ходе последующих выкладок происходит как
бы перадресация статуса между ![]() и
и ![]() А именно, область значений оператора
А именно, область значений оператора ![]() начинает выступать в качестве свободного
члена и задача, в значительной мере, сводится к нахождению по нему функции
начинает выступать в качестве свободного
члена и задача, в значительной мере, сводится к нахождению по нему функции ![]() При этом незамкнутость
При этом незамкнутость ![]() – значения не имеет.
– значения не имеет.
Обратим внимание, вследствие
(21) определение функции ![]() удовлетворяющей уравнению (1), осуществляется
под, образно выражаясь, «материализованным прессингом» на предмет соблюдения
абстрактной, казалось бы, теоремы Банаха об обратном операторе. Конкретно, этим
занимается тождественный оператор из
удовлетворяющей уравнению (1), осуществляется
под, образно выражаясь, «материализованным прессингом» на предмет соблюдения
абстрактной, казалось бы, теоремы Банаха об обратном операторе. Конкретно, этим
занимается тождественный оператор из ![]() обеспечивая вхождение упомянутой
функции в явном виде.
обеспечивая вхождение упомянутой
функции в явном виде.
Показано, что к итегральным уравнениям Фредгольма первого рода легко сводятся широкие классы задач математического моделирования. После этого, процедура корректной постановки и конструктивной реализации, оговоренная для одномерного случая, распространяется на них – непосредственно. Тем самым, до некоторой степени утрачивает смысл дифференциация постановок задач математической физики на прямые и обратные. Предложен также способ проверки на разрешимость задач, сформулированных в категориях уравнений с частными производными.
В свете изложенного, представляется возможным сделать следующий вывод. Если явление (процесс) в прямой постановке – определение следствия – допускает адекватное описание средствами математического моделирования, восстановление его побудительных причин не содержит принципиальных затруднений, так как соответствующие задачи могут быть поставлены корректно. С этой точки зрения, анализ реально наблюдаемых событий, включая многофакторные социально-экономические и экологические процессы, способен поизводится с гораздо большей эффективностью.
Не следует ли предположить, что и вообще процесс познания Мира значительно проще, нежели о нем принято судить в широкой аудитории под впечатлением отзвуков из сферы научного обслуживания. Последняя, на современном этапе, вооружившись средствами электронной обработки информации, кажется естественной монополией с едва ли не доминантной ролью коммерческого компонента, а соответственно и системной устремленностью к высокой стоимости исследований?
Так,
колоссальные средства расходуются на задачи восстановления зависимостей по эмпирическим
данным и, в частности, дистанционное зондирование поверхности Земли средствами
космического базирования. При этом фактически осуществляется эмпирический поиск
минимально и максимально приемлемого значения параметра ![]() в интегральном уравнении
вида
в интегральном уравнении
вида
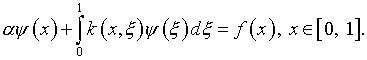
Суть
в необходимости установления паритета на стыке вычислительных, а соответственно
и финансовых возможностей решения почти вырожденной алгебраической задачи, и
приближением к «точной» постановке, которая отождествляется с фактором некорректности
при ![]()
Заметим в этой связи, что, конечно, не следует полагать будто бы научные проблемы отсутствуют вообще, или же для их преодоления, независимо ни от чего, могут быть выработаны эффективные средства. Однако, представляется, что осложнения принципиального характера присущи прямым постановкам задач, подразумевающим построение математических моделей недостаточно изученных процессов и явлений.
Понятно, что при решении обратных задач математического моделирования также могут возникать существенные препятствия и, тем не менее, догма об объективной некорректности процедуры восстановления причины по следствию, в целом, представляется глубоко ошибочной.
Утверждение Ж.Адамара о корректности задач, адекватно описывающих реальные явления, явилось гениальным предначертанием, конструктивное воплощение которого позволит вывести потенциал средств математического моделирования на качественно более высокий уровень.
2 марта 2005 г.