4.           МЕТОД СВЕДЕНИЯ ЗАДАЧ, ТРАДИЦИОННО ОТОЖДЕСТВЛЯЕМЫХ С ИНТЕГРАЛЬНЫМИ УРАВНЕНИЯМИ ФРЕДГОЛЬМА ПЕРВОГО РОДА, К РЕШЕНИЮ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ ФРЕДГОЛЬМА ВТОРОГО РОДА

4.3.         Трансформированная постановка задачи

Распространим уравнение (4.4) при условии (4.6) следующим образом:

где  вследствие (4.14), – некоторая неопределенная функция.

Уравнение, объединяющее (4.7) и (4.23), представим в виде

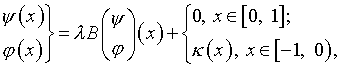                                      (4.24)
то есть

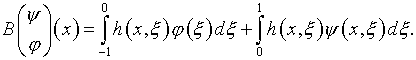
Введем также взаимосвязанное с ним и близкое по своей структуре уравнение:

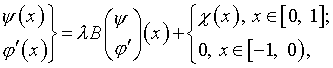                                        (4.25)
где  и  – еще две неопределенные функции (как и  они – гармонические). Целесообразность такого шага будет раскрыта в процессе дальнейшего изложения.

Представить процедуру построения уравнений (4.24) и (4.25), с практической точки зрения, несложно. Есть гармоническая функция  которая интегрируется согласно (4.1). Как показано выше, существуют ядро  и абсолютно интегрируемая функция  при которых уравнение (4.24) удовлетворяется на  Можно предположить, что каким-то образом функция  определена. Теперь как  так и  – данные функции. Уравнение (4.24) на  а также и в целом удовлетворяется посредством функции

Вновь дана  Функция  определяется из уравнения (4.25) на :

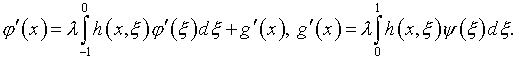   (4.26)

Относительно  – это интегральное уравнение Фредгольма второго рода. На основании положений общей теории [1], при условии (4.18) решение уравнения (4.26) существует и единственно. Есть данные функции   –  уравнение (4.25) на  и в целом удовлетворяется посредством

Если использовать обозначения

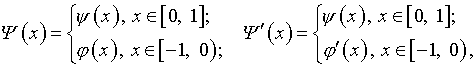           (4.27)
то (4.24), (4.25) представляют собой интегральные уравнения Фредгольма второго рода относительно   и  со свободными членами соответственно

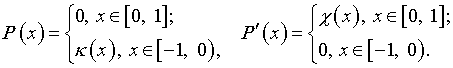
При условии (4.20) решения этих уравнений:

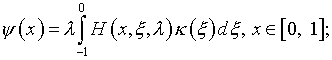                                        (4.28)

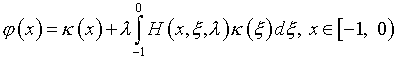                           (4.29)

и

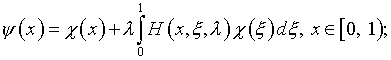                            (4.30)

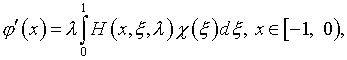                                     (4.31)

где  – резольвента оператора  имеющая вид (4.21).

Вычитая (4.25) из уравнения (4.24), получаем

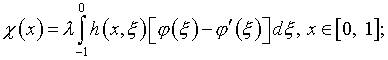                             (4.32)

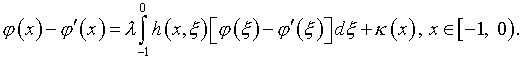  (4.33)

Из этих соотношений следует, что функцию  через  можно выразить конструктивно, то есть с помощью решения интегрального уравнения Фредгольма второго рода. Действительно, при условии (4.18)  определяется через резольвенту ядра  в (4.33). Однако обратная процедура, то есть представление функции  через  была бы сопряжена с решением интегрального уравнения Фредгольма первого рода.

К уравнениям (4.24), (4.25) прибавим «нуль» из (4.1), а именно  со свободным членом вида (4.22), получая соответственно

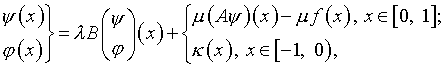                  (4.34)

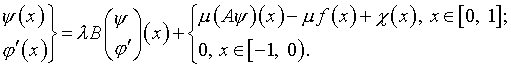    (4.35)

Итак, вместо некорректной задачи (4.1), далее будут рассматриваться две системы интегральных уравнений (4.24), (4.34) и (4.25), (4.35).*