| |
|
|
|
1.2. Постулат Адамара и некорректность «реальных» задач
1.3. Теорема Банаха об обратном операторе в аспекте корректности
1.4. Предпосылки реализации условий корректности
Жак Адамар определил два условия, которым должна удовлетворять корректно поставленная краевая (начально-краевая) задача для уравнений с частными производными: существование и единственность решения [1, c.12].* Вместе с тем, хорошо известно о третьем условии корректности по Адамару в отношении непрерывной зависимости решения от данных задачи. Действительно, он уделил пристальное внимание исследованию этого вопроса применительно к теореме Коши-Ковалевской, посвященной решению дифференциального уравнения
 |
(1.1) |
(системы аналогичных уравнений), где 
– аналитическая
функция своих аргументов в окрестности начала координат, с начальными условиями
 |
(1.2) |
Как отметил Ж.Адамар, при рассмотрении задачи (1.1), (1.2), носящей имя Коши, возникают три следующие вопроса [1, c.17]:
1) Имеет ли она решение?
2) Является ли решение единственным? (В совокупности, корректно ли поставлена задача?).
3) Наконец, как вычислить это решение?
Теорема Коши-Ковалевской (в ее авторской интерпретации)
утверждает, что, за исключением ряда особых случаев, данная задача имеет единственное
решение, аналитическое вблизи начала координат. При этом функции 
в (1.2) могут быть не только
аналитическими, но и регулярными, то есть непрерывными со своими производными
до некоторого порядка. Подразумевается возможность равномерного приближения
функций
рядами Тейлора по степеням 
в связи с чем на них переносятся все операции с аналитическими функциями, включая
дифференцирование до соответствующего порядка.
Однако такой подход встретил критику Адамара. По его мнению, вопрос заключается не в том, насколько подобная аппроксимация влияет на начальные условия, главное – как значительно в результате изменится решение? Подчеркнута неэквивалентность понятий малого возмущения для данных задачи Коши и ее решения [1, c.39]. В этой связи Адамар привел свой знаменитый пример о решении дифференциального уравнения
 |
(1.3) |
с условиями
 |
(1.4) |
где 
– функция,
быстро убывающая с ростом 
Выражение в правой части (1.4) может быть сколь угодно малым и, тем не менее, задача имеет решение
 |
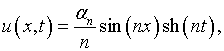(1.5) |
которое если 
или 
или 
– весьма велико для любого значения 
отличного от нуля (вследствие превалирующего роста 
и соответственно 
). Итак, функция (1.5)
не зависит непрерывно от начального условия и, следовательно, задача (1.3),
(1.4) является некорректной.
О регулярности правых частей (1.2) Адамар заметил: «… поистине один из наиболее любопытных фактов теории заключается в том, что уравнения, по виду очень близкие, ведут себя совершенно противоположным образом» [1, c.29].
Вопросам корректной постановки задачи Коши посвящено большое количество исследований, авторы которых занимались как выделением соответствующих классов дифференциальных уравнений, так и минимизацией ограничений, предъявляемых к начальным условиям (см. [2]). Однако нас более всего интересует, собственно, характер зависимости решения от данных задачи и, с этой точки зрения, классическое утверждение Адамара: «Аналитическая задача всегда корректно поставлена в смысле, указанном ранее, когда есть механическое или физическое истолкование вопроса» [1, c.38].
Как отметили В.Я.Арсенин и А.Н.Тихонов [3],
последнее поставило под сомнение целесообразность изучения некорректных задач,
к которым авторы отнесли: решение интегральных уравнений первого рода; дифференцирование
функций, известных приближенно; численное суммирование рядов Фурье, когда их
коэффициенты известны приближенно в метрике 
аналитическое продолжение функций; решение обратных задач гравиметрии, а также
плохо обусловленных систем линейных алгебраических уравнений; минимизацию функционалов
в условиях несходящихся последовательностей координатных элементов; некоторые
задачи линейного программирования и оптимального управления; проектирование
оптимальных систем и, в частности, синтез антенн. Подчеркнуто, что это далеко
не полный перечень, так как некорректные задачи возникают при исследовании широчайшего
спектра проблем физики и техники.
Г.Е.Шилов в выступлении на заседании Московского математического общества, посвященном памяти Адамара [4], высказал следующее: «Наше время внесло коррективы в установки Адамара, поскольку выяснилось, что некорректные по Адамару задачи могут быть содержательными (как, например, задача о восстановлении потенциала поля по данным рассеяния); но, конечно, изучение корректных задач, провозглашенное Адамаром, явилось цементирующим средством для формирования всей теории» (имеется в виду функциональный анализ). Данная цитата заимствована из биографического очерка Е.М.Полищука и Т.О.Шапошниковой [5], в котором также отмечено, что с течением времени мнение Адамара о важности для практики только корректных задач стали понимать не столь абсолютно.
Вместе с тем делались и достаточно резкие заявления:
«Более того, Адамар выдвинул утверждение о том, что некорректные задачи вообще не имеют смысла. А поскольку (как это видно с современных позиций) большинство прикладных задач, описываемых уравнениями первого рода, являются некорректными, то данное утверждение выдающегося математика, по-видимому, сильно затормозило в 20–50 гг. ХХ века развитие теории, методов и практики решения указанного класса задач» [6, c.12].
«До последнего времени считалось, что некорректные задачи лишены физического смысла и их не имеет смысла решать. Однако имеется много важных прикладных задач физики, техники, геологии, астрономии, механики и т.д., математически описываемых адекватно и, тем не менее, являющихся некорректными, что сделало актуальной проблему разработки эффективных методов их решения» [6, c.225].*
«Из результатов этой работы [А.Н.Тихонова] следовала ограниченность известного понятия Ж.Адамара [1] корректно поставленной задачи математической физики, имеющего безусловный методологический интерес, и несостоятельность тезиса Адамара, получившего широкое распространение среди исследователей, о нефизичности всякой некорректно поставленной математической задачи» [7, c.3].
«К области метафизики долгое время было принято (в том числе и очень крупными математиками) относить деятельность, связанную с анализом и решением задач, которые получили название некорректных» [8, c.126]. «Преобладающее большинство математиков, в том числе и Адамар, выразило свое отношение к данной проблеме следующим образом: если некоторая задача не удовлетворяет требованиям корректности, то она не представляет никакого практического интереса, а стало быть, ее незачем решать» [8, c.127] (автор раздела «Некорректные задачи математической физики» – Н.Г.Преображенский).
Заметим, что в последней из указанных работ наиболее рельефно просматривается стиль, вызывающий принципиальное возражение. Так, А.Пуанкаре обвинен в несостоятельности методологических воззрений о природе причинно-следственных связей [9] («Последние мысли»). Действительно, текст не содержит сведений, которые бы свидетельствовали о фетишизации им проблемы восстановления причины по следствию. Из этого делается вывод о недопонимании великим ученым существа неустойчивости вычислительных процедур, органично присущих некорректным задачам и, в частности, интегральным уравнениям первого рода.*
Адекватность обсуждаемых моделей реалиям авторами [8] никак не затрагивается и возникает вполне закономерный вопрос: из чего следует, что Пуанкаре, при необходимости, не нашел бы способа математически корректной постановки тех же физических задач? В любом случае, чему противоречат общие соображения о существовании подобной возможности, включая аспекты ее практической реализации?
Кстати, именно Пуанкаре неоднократно упоминает Адамар, выясняя взаимосвязь между корректной постановкой задач и адекватностью используемых моделей. Обратим внимание на весьма красноречивый тезис: «Если физическая задача сводится к аналитической, такой как (1.3), (1.4), то нам будет казаться, что ею управляет чистый случай (согласно Пуанкаре, это состоит в том, что детерминизм нарушается), и она не подчиняется никакому закону» [1, c.43].
В свете сказанного, представляют интерес соображения И.Пригожина и И.Стенгерс [10]: «… о «физическом законе» какого-нибудь явления можно говорить лишь в том случае, когда этот закон является «грубым» относительно предельного перехода от описания с конечной точностью к бесконечно точному и в силу этого недостижимому для любого наблюдателя, кем бы он ни был» (с.9). «Ученые на сотни различных ладов выражали свое изумление по поводу того, что при правильной постановке вопроса им удается разгадать любую головоломку, которую задает природа» (с.44).
Итак, подчеркнуты: во-первых, методологическая значимость корректных постановок задач математической физики; во-вторых, главенствующая роль используемых для этого процедур и, наконец, влияние эффективности их реализации на степень сложности получения конечного результата. Таким образом, одна и та же задача может быть лучше или хуже поставлена.
Приведенное выше утверждение или, как его назвал С.К.Годунов, – постулат Адамара [11, с.113], по существу, подразумевает возможность «хорошей» (корректной) постановки любой физически содержательной задачи и, следовательно, имеет глобальную значимость.*
В этой связи очевидна созвучность с комментариями Д.Гильберта к сформулированной им 20-й проблеме, предположившего возможность корректной постановки произвольных краевых задач математической физики посредством специальных требований к граничным значениям соответствующих функций (типа непрерывности или кусочной дифференцируемости до определенного порядка), а при необходимости – и придания понятию решения расширительного толкования [12, c.54-55].
Впервые три условия корректности краевых задач математической
физики отчетливо указали Д.Гильберт и Р.Курант [13,
c.199-200]: существование, однозначная определенность и непрерывная зависимость
решения от данных задачи. Относительно последнего условия сказано:
«… оно
имеет коренное значение и отнюдь не является тривиальным. … Математическая задача
лишь в том случае может считаться адекватной для описания реальных явлений, если
изменению предложенных данных в достаточно тесных пределах соответствует также
малое, т.е. ограниченное заранее заданными пределами, изменение решения».
Совершенно аналогична позиция В.А.Стеклова [14, c.62]: «… если дифференциальные уравнения с упомянутыми выше начальными и предельными условиями построены не на ошибочных основаниях, не находятся в явном противоречии с действительностью, то они должны давать для каждой задачи единственный и вполне определенный ответ …», а также И.Г.Петровского [15, c.87]: «Приведенные выше соображения о корректности постановки задачи Коши показывают, что и другие краевые задачи для уравнений с частными производными представляют интерес для естествознания только в том случае, если имеет место, в некотором смысле, непрерывная зависимость решения от краевых условий, корректность постановки задачи».
С.Л.Соболев не столь категоричен [16, c.38]: «Решение задачи, некорректно поставленной, в большинстве случаев не имеет практической ценности». Весьма интересно мнение В.С.Владимирова [17, c.69]: «Проблема нахождения корректных постановок задач математической физики и методов их решения (точных или приближенных) составляет основное содержание предмета уравнений математической физики».
В.В.Новожилов по существу обратил внимание на потенциал видоизменения постановки задачи с целью упрощения процедуры ее численной реализации [18, c.352]: «Отсутствие в термине «математическая модель» указания на ее неизбежную приближенность дает повод формально-математического подхода к моделям в отрыве от тех конкретных задач, для решения которых они предназначены, что, к сожалению, в настоящее время распространено».
Итак, Адамар и целый ряд других выдающихся ученых полагали, что любая физически интерпретируемая задача может быть корректно поставлена, но в современных изданиях превалирует совершенно противоположная точка зрения. В самом деле, большая часть практически важных задач, которые в них рассматриваются, - некорректны. Однако адекватна ли собственно методология математической постановки этих задач, а соответственно и результаты ее преломления к реалиям?
Здесь не стоит углубляться в нечто вроде общих принципов построения дифференциальных уравнений и, вообще говоря, вначале вопрос целесообразно сузить: из каких соображений судят о том, что некорректно поставленная задача действительно описывает наблюдаемое явление, или же потенциально реалистичный процесс? В этой связи обратимся к процедуре решения интегрального уравнения Фредгольма первого рода
 |
(1.6) |
– классической некорректной задаче: квадратично суммируемые
ядро 
и свободный
член 
– даны;
функция 
– подлежит
определению.
Предположим, что ядро симметрично и замкнуто, то есть
собственные
функции 
представляющие
собой нетривиальные решения интегрального уравнения
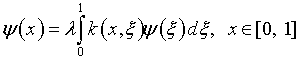
с характеристическими
числами 
образуют полную в 
систему элементов. В этом случае решение уравнения (1.6)
существует и единственно при условии [19,
с.185-187]:
 |
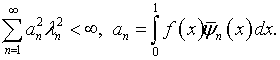(1.7) |
Если все указанные требования выполнены, то остается
третье условие корректности, которому, как известно, уравнение (1.6)
заведомо не удовлетворяет. Многочисленные руководства наглядно демонстрируют
неадекватно сильное влияние на решение малых возмущений данных задачи, в первую
очередь 
Зачастую эта функция определяется экспериментально и не согласована с ядром
в частности по гладкости, а, следовательно, уравнение (1.6)
вообще утрачивает смысл. Вместе с тем возможность эквивалентного описания задач
математической физики посредством интегральных уравнений первого рода в настоящее
время считается несомненной, о чем свидетельствует их колоссальный перечень
[6, п.4.2].
Конкретизируем уравнение (1.6):
 |
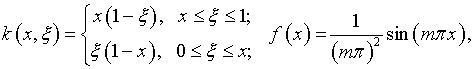(1.8) |
где
– целое
положительное число. При этом 
[20,
с.149].
Поскольку ядро 
– симметрично, непрерывно и все 
использование теоремы Мерсера [19],
согласно которой
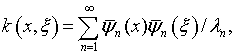
а также представление
в виде ряда с неопределенными коэффициентами по элементам
позволяют найти решение уравнения (1.6)
 |
(1.9) |
Но столь простой, вычислительная процедура оказалась
вследствие специального выбора данных задачи. В противном случае, или же при
решении уравнения (1.6)
с ядром и свободным членом (1.8)
одним из численных методов, сложность реализации достаточно высокого приближения
– практически идентична наиболее общей ситуации, характеризующейся погрешностью
задания
и 
* Суть в том, что даже при объективной совместимости данных,
некорректность уравнения (1.6)
проявляется вследствие округления цифр при проведении вычислений.
Фактор некорректности уравнения (1.6)
вытекает из сопоставления свободного члена (1.8)
с решением (1.9). В самом
деле, с увеличением
функция
может оказаться сколь угодно малой, тогда как пределы значений
– неизменны. Соответственно та, или иная погрешность вычислительных операций
со свободным членом
проецируется на функцию 
имея множитель 
Механизм этого феномена сглаживания информации о функции при ее интегрировании
будет неоднократно затронут в ходе дальнейшего изложения.
Однако вернемся к сформулированному вопросу о сопряжении
некорректной постановки с реальностью и, в этой связи, обратим внимание на следующее
обстоятельство. Рассматривая (1.6)
в качестве интегрального уравнения Фредгольма первого рода, мы подразумеваем
решение обратной задачи (О). Но (1.6)
можно использовать и для решения соответствующей прямой задачи (П): вычисление
функции
по данным
и 
Эта процедура корректна, а значит – радикально проще задачи О. Достаточно заметить,
что отсутствует принципиальное различие между вычислением интеграла (1.6)
в аналитическом виде и его сугубо численной реализацией.
И здесь хотелось бы привлечь внимание к моменту, который
представляется весьма существенным. Задача П, как правило, прозрачна – в ее категориях
мы адекватно моделируем реально происходящие процессы и явления наглядными, что
важно подчеркнуть, средствами линейной суперпозиции. Соответственно если, например,
– характеристика
системы, а – интенсивность
внешнего воздействия, то результат события в той, или иной предметной области
остается лишь элементарно просуммировать.
Ситуация с задачей О – диаметрально противоположна. Едва ли представляется возможным указать реальный процесс (явление), для которого ее удавалось бы формулировать математически, – непосредственно из соображений предметной области. Иначе говоря, вне привязки к задаче П, наряду с чем общепринятой является трансформация последней в задачу О путем, всего лишь, переименования известных и неизвестных компонентов.
Как представляется, ущербна методология, в рамках которой на основании вполне доброкачественной информации о конкретной задаче П говорится об адекватности реалиям задачи О, полученной с помощью упомянутого переименования компонентов. Соответственно ничем не подкрепленными следует считать суждения специалистов, априори отвергающих утверждение Адамара о существовании корректных постановок задач математической физики.
Обратимся к задаче П, описывающей некоторый реальный
процесс (явление) (1.6).
Для него, конечно же, имеет смысл определение функции
по данным
и 
то есть постановка и решение соответствующей обратной задачи, которую обозначим
через О'. Предположим, что в рассматриваемом случае утверждение Адамара имеет
место и, следовательно, задача О' – корректна. Но задача О – решение интегрального
уравнения Фредгольма первого рода (1.6)
– некорректна по определению.
Вывод очевиден: математические формулировки (представления,
выражения) задач О и О' – нетождественны. Следовательно, постановка задачи О'
не может ограничиваться лишь переадресацией статуса неизвестной между функциями
и 
в
задаче П. Заметим в этой связи, что развитие методологии корректной постановки
задачи, обратной П, то есть О,' является главной целью настоящего исследования.
Приведенные доводы кажутся достаточно весомыми, однако
на данном этапе изложения не представляется возможным как доказать правомерность
постулата (утверждения) Адамара в общем случае, так и проиллюстрировать его реализацию
применительно к отдельным классам задач. Следует также учесть, что, используя
специальные приемы, решение некорректной задачи О (или то, что под ним подразумевается)
зачастую удается получать с точностью, которую считают практически приемлемой.
В связи с этим возникает вопрос: следует ли стремиться к корректной постановке
О', если алгоритмы вычисления функции в постановке
задачи О так или иначе осуществляют ее регуляризацию? Имеется в виду известная
деформация постановки О с использованием малого параметра, сообщающая ей свойства
корректной разрешимости.
Итак, способен ли алгоритм в полной мере, включая эффективность процедуры его численной реализации, нивелировать принципиальные осложнения, заложенные некорректностью задачи О вида (1.6)? Понятно, что ответ может быть только отрицательным, – в противном случае утратила бы смысл прочно устоявшаяся дифференциация задач на корректно и некорректно поставленные.
Более того, обозначенное расхождение является исключительно существенным, поскольку корректность постановки – критерий качественного уровня, что же касается эффективности метода решения интегрального уравнения Фредгольма первого рода, то его можно измерять лишь в количественных показателях паллиативного свойства. Сказанное обуславливается непосредственной взаимозависимостью между глубиной регуляризации и деформацией (искажением) задачи О.
Однако в чем собственно может выражаться разночтение постановок О и О'? Ответ на этот вопрос содержится в пп. 3.5, 4 и 5. Заметим лишь, что трансформация постановки О в О' будет осуществляться посредством не вполне непрерывного возмущения интегрального оператора задачи (1.6), моделирующего феномен сглаживания информации процедурой интегрирования.
Приведем выдержку из [5, c.175]: «Первоначально Адамар определял корректность задачи лишь условиями разрешимости и единственности, энергично настаивая на непрерывной зависимости решения от начальных данных только при обсуждении задачи Коши. Вот что он написал в книге «Теория уравнений в частных производных», вышедшей в Пекине через год после его смерти: «Это третье условие, которое мы ввели в «Лекциях о задаче Коши …», но не рассматривали как часть определения хорошо поставленных задач, было присоединено, и совершенно справедливо, Гильбертом и Курантом [13]. Мы принимаем здесь их точку зрения».
Е.М.Полищук и Т.О.Шапошникова сопроводили этот текст комментарием [5, с.175-176]: «С математической точки зрения вопрос о необходимости включения требования непрерывности решения относительно данных представляется довольно деликатным. Дело в том, что согласно известной теореме Банаха о замкнутом графике, однозначная разрешимость линейной задачи влечет ограниченность обратного оператора, а тем самым – и непрерывную зависимость решения от правых частей». Отмечено, что на решение задачи могут также влиять вариации коэффициентов дифференциальных уравнений и контура области определения, вследствие чего использование трех условий корректности является предпочтительным.
Вместе с тем к рассматриваемой проблематике в большей
мере относится теорема Банаха об обратном операторе [21,
c.34], являющаяся следствием указанной выше. Ее формулировка, данная А.Н.Колмогоровым
и С.В.Фоминым, гласит [22,
c.259-260]: Пусть 
– линейный ограниченный оператор, взаимно однозначно отображающий банахово пространство
на банахово пространство 
Тогда обратный оператор 
– ограничен.
Л.А.Люстерник и В.И.Соболев [23,
c.159-161] в дополнение подчеркнули, что подразумевается взаимно однозначное
отображение всего банахова пространства
на все банахово пространство
Наряду с этим оговорена ситуация, при которой «… оператор, обратный
к ограниченному линейному оператору, оказывается хотя и линейным, но определенным
не на всем пространстве 
а лишь на некотором линейном многообразии и неограниченным на этом многообразии».
Формулировка той же теоремы в [24,
c.60] такова: Если линейный ограниченный оператор 
отображающий банахово пространство
на все банахово пространство
имеет обратный – 
то
ограничен. При этом отмечено, что данное утверждение утрачивает силу, если отказаться
от полноты одного из указанных пространств. Приведено также пояснение: из существования
и единственности решения уравнения 
при всякой правой части из 
следует непрерывная зависимость решения 
от 
Сам Банах высказался так: Если линейная операция преобразует
взаимно однозначно на
то
преобразование является взаимно непрерывным. При этом в формулировке теоремы о
замкнутом графике он отметил, что преобразование осуществляется
на все пространство
Л.В.Канторович и Г.П.Акилов внесли уточнение, касающееся
отображения на замкнутое подпространство банахова пространства
[25, c.454]. Смысл в
том, что замкнутое подпространство банахова пространства само является банаховым
пространством.
С.Г.Михлин привел доказательство теоремы [26,
c.507]: Для того, чтобы линейная задача
была корректной в паре банаховых пространств 
необходимо и достаточно существование ограниченного оператора
отображающего все пространство
на 
При этом четко разграничены категории существования и единственности
решения краевой задачи с ее корректностью в целом, предполагающей как следствие,
непрерывность зависимости от данных (третье условие по Адамару). Дано определение:
«Краевая задача называется корректной в паре банаховых пространств
и
если ее решение единственно в
и существует при любых данных из
и если достаточно малому изменению начальных данных в норме
соответствует сколь угодно малое изменение решения в норме
» (с.204).
Автор отметил, что задача может оказаться корректной
в одной паре пространств и некорректной в другой. При этом некорректность интегрального
уравнения Фредгольма первого рода (1.6)
вытекает из противного: если задача корректна – существует ограниченный оператор
и, следовательно, тождественный оператор 
вполне непрерывен в соответствующем бесконечномерном пространстве,
что противоречит положениям общей теории [24].
Михлин также вполне благосклонно отозвался о направлении приближенного решения
некорректных задач, возглавляемом А.Н.Тихоновым.
В аналогичном по содержанию курсе [27,
с.169-172] Михлин повторил приведенные формулировки, однако Тихонов не упомянут
вовсе, тогда как обсуждение уравнения (1.6)
получило весьма интересное продолжение (с.171). Показано как задача его разрешения
становится корректной, если пару пространств 
заменить на такую, в которой оператор
уже не будет вполне непрерывным. Общие соображения проиллюстрированы
примером. Пусть
и
удовлетворяют условиям п.1.2, включая (1.7).
Оказывается, если в качестве
сохранить 
а
принять также гильбертовым пространством функций, нормированных согласно
(1.7), то решение уравнения
(1.6) превращается в корректно
поставленную задачу: оператор
– не вполне непрерывный и
– ограничен.
В этой связи можно отметить, что оператор
ограниченно обратим не только когда он действует из
на все гильбертово пространство
Достаточно, чтобы оператор
был ограничен снизу и его область значений 
была всюду плотной в
Вместе с тем,
– не обязательно замкнута [28,
с.34].
Спустя еще одно десятилетие, Михлин фактически отказался от исследований, связанных с проблемой корректности [29]: «Автор придерживается классической точки зрения, по которой задача, к решению которой применяются математические методы, должна рассматриваться как поставленная точно. Конечно, существуют и другие мнения (с.7). … Тем самым мы пренебрегаем так называемыми неустранимыми погрешностями, связанными с постановкой упомянутой задачи как задачи естествознания или социально-научных дисциплин (погрешности измерений, недостаточная точность основных гипотез и т.п.)» (с.17).
М.М.Лаврентьев и Л.Я.Савельев охарактеризовали исследование
вопроса о разрешимости уравнения (1.6)
с привлечением соображений по типу [27]
как тривиальное, поскольку при экспериментальном определении
трудно представить, чтобы возникающая погрешность оказалась малой в норме пространства
[30, c.217]. Наряду
с этим отмечается, что, вообще говоря, для любого операторного уравнения можно
подобрать пары пространств, в которых задача его разрешения была бы корректной.
Г.М.Вайникко и А.Ю.Веретенников обратили внимание на сложность описания таких пространств. Так, даже интегральное уравнение Вольтерра первого рода
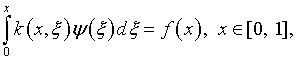
допускающее регуляризацию:
и элементарно разрешимое
в квадратурах, по соображениям нормы для
зачастую, приходится рассматривать как некорректно поставленную задачу [31,
c.6].
В отношении пары пространств, реализующих условия корректной постановки, представляет интерес замечание К.И.Бабенко [32, c.304]: «Известный пример Адамара (1.3), (1.4), дающий решение задачи Коши вида (1.5), говорит вовсе не об отсутствии непрерывной зависимости от начальных данных, как его обычно трактуют, а о том, что малые изменения начальных данных могут привести к тому, что мы выходим из совокупности начальных данных, для которых существует решение задачи Коши».
Кстати, Р.Рихтмайер продемонстрировал корректность процедуры численной реализации весьма сложной задачи указанного типа путем представления искомых функций двумерными степенными рядами и реализации специальных приемов подавления погрешности арифметических операций [33, п.17.В].
Две следующие теоремы приведены в курсе В.А.Треногина [34, c.225]:
Пусть 
и 
– бесконечномерные
нормированные пространства, причем полно.
Если – вполне
непрерывный линейный оператор из в 
отличный
от конечномерного, то его область значений не
является замкнутым множеством в 
Пусть – вполне
непрерывный оператор из бесконечномерного нормированного пространства в нормированное
пространство причем
на существует
обратный оператор 
Тогда
неограничен
на 
Предположим, что 
– точный результат интегрирования функции 
и симметричного замкнутого ядра
по формуле (1.6):
 |
(1.10) |
Однако в общем случае, правая часть этого уравнения является реально следующей:
 |
(1.11) |
где 
– допускаемая погрешность.* При этом, естественно,
не принадлежит области значений оператора
определяемой условием (1.7).
Далее пространство функций, для которых оно выполнимо, будет обозначаться через
В отличие от обычного 
принадлежность 
зависит как от функции
так и оператора 
Таким образом,
– пространство функций, получаемых в результате интегрирования по формуле (1.6)
данного ядра
и всего множества
из 
Собственно говоря,
и
в рассматриваемом случае – одно и то же. Вместе с тем, понятие пространства
в большей мере характеризует вид нормирующего функционала (1.7).
Между
и такой абстракцией, как область значений оператора
– теорема Пикара, дающая условие разрешимости уравнения (1.6)
[20]. Кроме того, полезным
может оказаться сопоставление
с пространством
тесная взаимосвязь которого с 
определяется теоремой Рисса-Фишера [19].
Напротив, свободный член уравнения (1.10)
и, вместе с тем, одна лишь проверка условия (1.7)
может оказаться неосуществимой из-за накопления погрешности вычислений. Своеобразная
«размытость» пространства
обуславливается структурой его нормирующего функционала. В этом смысле пространство
является для функции
гораздо более осязаемым и, тем не менее, его использование влечет весьма негативные
последствия.
Действительно, в таком случае
не принадлежит замкнутому подпространству
операторы
и
соответственно – вполне непрерывный и неограниченный, вследствие чего
процедура численной реализации уравнения (1.6),
по существу, выводится из сферы применения фундаментальной теоремы Банаха об
обратном операторе. Не слишком ли дорогая расплата за эфемерную, как представляется,
наглядность при постановке задачи в условиях отображения внутри пространства
?
Обратим внимание на известную точку зрения о необходимости выбора пространств, которым принадлежат данные задач математической физики, исходя из практических приложений, с которой трудно не согласиться. Вместе с тем достаточно спорным можно назвать также распространенное мнение будто бы социолог, например, должен ставить задачу, решаемую затем математическими методами, с указанием, в частности, пространств, которым принадлежат ее данные. Последнее, как правило, допускает вариативность, создающую предпосылки повышения эффективности процедур численной реализации.
Имеются ли перспективы преодоления оговоренной сложности
сопряжения свободного члена уравнения (1.6)
с адекватным ему пространством
? В этой связи обратимся к уравнению (1.10),
которое с учетом (1.11)
приобретает вид
 |
(1.12) |
Однако, есть шанс приведения данной функции
к 
посредством адаптивного моделирования погрешности 
Действительно, ее можно трактовать как сглаживание информации процедурой интегрирования.
Исходя из этого,
представляется целесообразным выразить разностью между искомой функцией
в явном виде и интегралом с ее участием, ядро которого не налагало бы на решение
задачи существенных ограничений. Одновременно, поскольку погрешность интегрирования
по формуле (1.6) объективно
невелика, вырисовывается условие вида
 |
(1.13) |
Итак, вместо отыскания функции
путем решения интегрального уравнения Фредгольма первого рода (1.6)
предлагается использовать возмущение 
приводящее к задаче (1.12),
(1.13). Тем самым создается
предпосылка для обеспечения 
* Как будет показано, с использованием также ряда дополнительных
соображений, определение функции
удовлетворяющей уравнению (1.6),
оказывается возможным свести к решению корректно поставленной задачи.
Заметим, что при значительном несоответствии между
и функцией
известной фактически, условие (1.13)
едва ли можно считать реально выполнимым. Тем не менее, намеченный подход остается
в силе, интерпретируя, образно выражаясь, приведение свободного члена уравнения
(1.6) к виду, при котором
оно разрешимо.
