|
|
|
|
|
Отмеченная следственность третьего условия корректности вытекает из теоремы
Банаха об обратном операторе [12], весьма оптимистичный смысл которой, состоит
в следующем. Если решение уравнения (3.1) с 
и 
где 
– банаховы пространства, существует и единственно,
то обратный оператор 
из 
в 
– ограничен (см. п.1.3).
Соответственно процедура вычисления функции
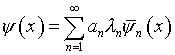(3.2)
(формула вытекает из теоремы Гильберта-Шмидта [13]), удовлетворяющей уравнению
(3.1) в 
должна быть устойчивой к малым возмущениям
и 
при условии 
Далее предполагается, что такая функция существует,
ядро симметрично и замкнуто; использованы
обозначения пп. 1.2, 1.4. Так, 
– гильбертово пространство функций,
нормированных согласно (1.7).
Следует отметить, что свойства интегрального уравнения Фредгольма первого
рода с симметричным ядром несложно перенести на случай, когда является произвольной функцией
из пространства 
[13, с.188-194].
Однако, как выполнение при проведении вычислений, так и проверка условия
– практически неосуществимы,
вследствие чего подобные пространства считают «неудобными» (см. [14, 15]). Налицо
принципиальная дилемма в выборе методологии исследования:
-
стремление к преодолению затруднений, обусловленных использованием пространства
в привязке к ограниченности
оператора 
- утрата данного свойства, взамен на возможность постановки и решения задач в «удобных» пространствах.
С началом широкомасштабного внедрения в математическое моделирование численных методов, второе из обозначенных направлений стало доминирующим.
Показательна динамика взглядов С.Г.Михлина, нашедшая отражение в его курсах
по математической физике и теории погрешностей 1968, 1977, 1988 гг. [16–18].
Вначале автор рассматривает уравнение (3.1) в традиционном предположении о том,
что оператор 
– вполне непрерывен. При этом обратный оператор
– неограничен, вследствие чего в обычном смысле
задача неразрешима и следует обращаться к методологии А.Н.Тихонова.
В дальнейшем Михлин привлек внимание к тому, что если интегральное уравнение
Фредгольма первого рода (3.1) трактовать с позиций отображения из пространства
в 
то оператор перестает быть вполне непрерывным, оператор
– ограничен, и задача определения функции
становится корректной. Одновременно воссоздается
целостность условий корректности, третье из которых автором изначально выделялось.
Итак, использование пары пространств 
– как бы переносит классическую
некорректно поставленную задачу в русло фундаментальных основ функционального
анализа. Обращает внимание тот факт, что Михлин не снизил значимость своих соображений
доводами об «удобных – неудобных», или же «хороших» и «плохих» пространствах.
Такая позиция, вероятно, встретила критику и в своей заключительной монографии Михлин раздраженно переадресует постановку задач математической физики прикладникам, которые заинтересованы в их разрешении, включая социологов. Одновременно он счел целесообразным не рассматривать бесконечномерные модели с характерной для них некорректностью.
Известно мнение А.М.Ляпунова о том, что, будучи сформулирована в рамках исходных предпосылок, задача механики или физики должна решаться затем строгими методами. При этом имеется в виду задача, «…которая поставлена совершенно определенно с точки зрения математики» [19, с.26]. То есть, надо понимать, – поставленная корректно.
Вместе с тем, почему бы собственно процедуру постановки задач математического моделирования не рассматривать в качестве средства повышения эффективности аппарата их численной реализации? Более того, не сообщают ли жестко детерминированные формулировки задач искусственные осложнения вычислительного свойства в условиях, когда из физических соображений допустимо малое, в некотором смысле, видоизменение? Как представляется, постановка задачи и алгоритм ее численной реализации представляют собой существенно взаимозависимые категории.
