5.           АНАЛИЗ И ДОПОЛНЕНИЕ МАТЕРИАЛОВ ПРЕДЫДУЩЕГО РАЗДЕЛА

5.3.         Второй вариант решения задачи

Здесь выкладки пп. 4.2 – 4.4 распространяются на случай, когда данные уравнения (4.1), то есть  и  а также удовлетворяющая ему функция  – изначально принадлежат пространству  Ядро  имеет прежний вид (4.13); параметр  – фиксирован.*

Обратимся к уравнению (4.24):

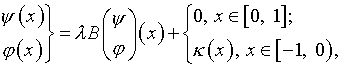                                      (5.19)
или

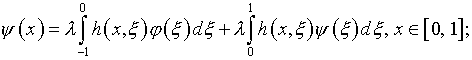            (5.20)

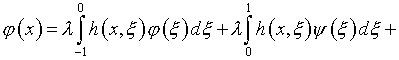
                                                                                    (5.21)
проистекающему из представления погрешности (4.4), при условии (4.6), и распространения (5.20) на

Возможность удовлетворения этому уравнению на интервале  с помощью  рассматривалась в п.4.2 (функция  выступала в качестве данной). Для того чтобы выполнить условие (4.6), подразумевающее приближение в пространстве  класс возможной принадлежности  пришлось ограничить гармоническими функциями.

При этом, по существу, вопрос сводится к исследованию разрешимости интегрального уравнения Фредгольма первого рода (4.10), определяемой условиями теоремы Пикара [2]:

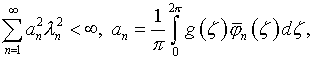                                            (5.22)
где  – характеристические числа и собственные функции ядра (4.11), перенумерованные в порядке их следования, см. (4.12). Кроме того, система собственных функций  должна быть полной на интервале  и ядро  – вещественным симметричным, что в данном случае заведомо имеет место.

И, тем не менее, как показал Э.Гурса [8, с.143-144], если даже условие (5.22) не выполняется, всегда можно найти такую функцию  что интеграл

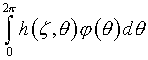
будет отличаться от  из (4.10), в среднем – сколь угодно мало. Следует отметить, что  при этом предполагается ядром гораздо более общего вида, нежели (4.11).

Доказательство основывается на совпадении

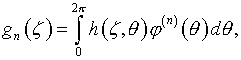
где

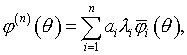 (5.23)
с суммой первых членов ряда Фурье функции  по элементам  Поэтому можно установить значение  при котором интеграл

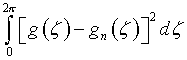
окажется меньше некоторого

Однако, удовлетворяя таким образом уравнению (4.10), с ростом  ряд (5.23) будет расходиться в пространстве  Соответственно не представляется возможным рассматривать (5.19) как интегральное уравнение Фредгольма второго рода относительно функции

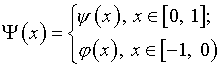                                                              (5.24)
и производить обращение оператора  Согласно позднее утвердившейся терминологии,  трактуется в качестве обобщенной функции – распределения [9, п.2.1.5; 10, п.12].

Итак, существует функция  удовлетворяющая уравнению (5.20), или же (4.7) в смысле

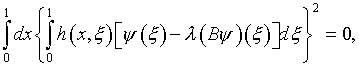
где оператор  имеет вид (4.5);  и произведена замена переменных (4.9).

Вместе с тем, фактически используемое ядро (4.13) – бесконечнодифференцируемо и периодически зависит от  что позволяет понимать  как обобщенную функцию в менее ограничительном смысле сходимости ряда (5.23) [11, с.17-18]:

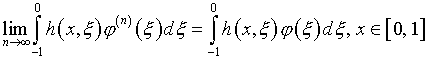                     (5.25)
(переменная  играет роль параметра).

Действительно, подстановка в (5.25) выражений (5.23) и (4.19), с использованием также (4.17) и переобозначения коэффициентов, сводится к следующему:

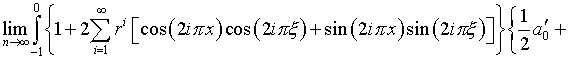
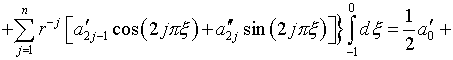
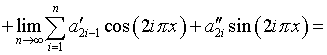
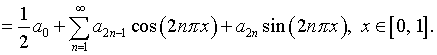
Далее функция  будет определяться из уравнения, построенного на базе соотношения (5.2).*

*  В отличие от п.4.4, где с аналогичной целью использовалось соотношение (4.32), приведшее к уравнению относительно функции

С использованием (4.39) оно принимает вид:

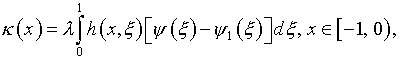                          (5.26)
где  – решение интегрального уравнения Фредгольма второго рода (4.40).

При этом в (5.26) совсем не обязательно подставлять функцию  из (4.28).*

* Действуя таким образом, мы пришли бы к уравнению (5.17), полученному в предположении о том, что функция  – гармоническая.

Достаточно выразить через  интеграл

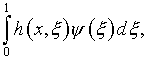
что равносильно приданию также и  смысла обобщенной функции.

Реализуя уже в объективно этом качестве  проинтегрируем с ядром  уравнения (5.20) и (5.21) в пределах соответственно  и  Получаем

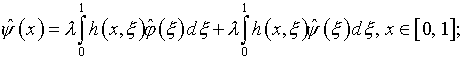              (5.27)

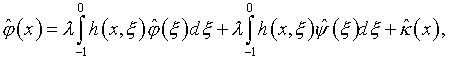
                                                                                                 (5.28)
где

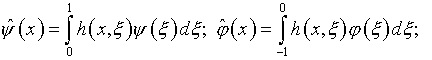
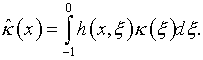                                                                           (5.29)

Поскольку

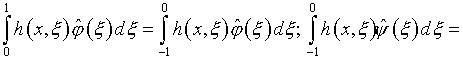
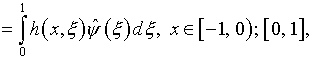
вследствие

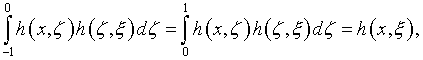
см. (4.19), уравнения (5.27) и (5.28) эквивалентны следующим:

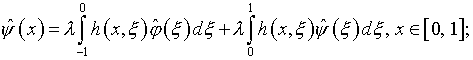
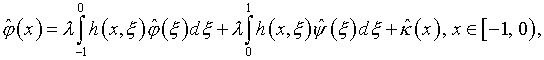
или

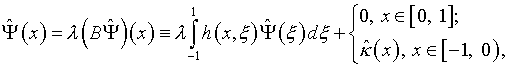     (5.30)
где

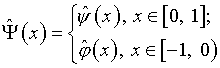                                                              (5.31)
(обратим внимание, вновь позитивную роль сыграл выбор ядра ).

То есть, получен точный аналог уравнения (5.19), в котором функция (5.24) заменена обобщенной – (5.31). Обращение оператора  в (5.30) дает

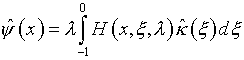
(аналог (4.28)), вследствие чего выражение (5.26), с учетом (5.29) и (5.18) приобретает вид:

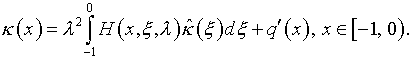
Подстановка  из (5.29), поскольку

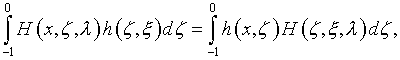
см. (4.53), (4.19) и (4.21), приводит к тому же самому уравнению (5.17). Таким образом, использование обобщенных функций обеспечило в данном случае законность выкладок, не оказав влияния на конечный результат их проведения.

Обратимся далее к уравнениям (4.34) и (4.35):

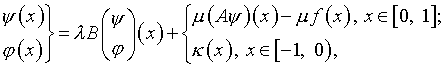                  (5.32)

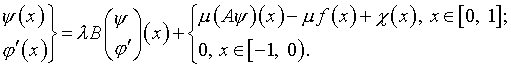    (5.33)
где  – оператор (4.5).

Как показано выше, превращение (5.33) в уравнение (5.32), или же наоборот, с помощью соотношений (4.32), (5.2), (5.3), а также других, позволяет получить интегральные уравнения Фредгольма второго рода (4.52), (5.17), решения которых, при соответствующем установлении параметров   существуют и единственны. Для конкретно выбранного ядра  будь-то выражение (4.13) или другое, они зависят исключительно от данных задачи.

Существуют и единственны в таком смысле и решения уравнений (5.32), (5.33), когда их свободные члены, включающие функции  предполагаются данными. Действительно, обращение в (5.32) оператора  приводит к интегральному уравнению Фредгольма второго рода:*

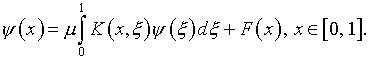                                 (5.34)

Здесь

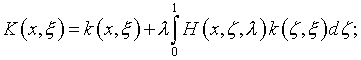                                  (5.35)

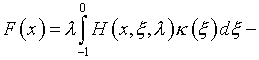
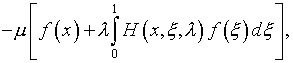                                                         (5.36)
где  – резольвента (4.21). Это уравнение отличается от (4.40) всего лишь компонентой свободного члена, и его решение находится аналогично. Зная  можно вычислить

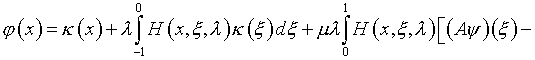
(то же самое нетрудно проделать и с уравнением (5.33)).

Входящая в выражение (5.36) функция  находится из уравнения (5.17), решение которого

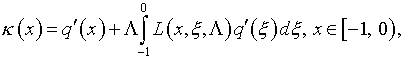                          (5.37)
где  – резольвента (4.56); функция  определяется выражением (5.18).

Последнее зависит от функции  которая, в свою очередь, представляет решение интегрального уравнения Фредгольма второго рода (4.40). При этом предполагается выполнение (4.59) – условий в отношении параметра   Значение  принимается так, чтобы уравнение (4.60) не имело нетривиальных решений.

Общая последовательность вычислительных процедур, после того как найдена функция  состоит в определении:

-  функции  – по формуле (5.18);

-  функции  – по формуле (5.37);*

* Заметим, что вне зависимости от данных (4.1) функция  – бесконечнодифференцируема.

- ядра и свободного члена уравнения (5.34) – по формулам (5.35), (5.36);

-  искомой функции  – из уравнения (5.34).

Доказательство удовлетворения получаемого таким образом решения уравнению (4.1) производится аналогично изложенному в п.4.5.

Кратко коснемся численной реализации уравнений (4.40) и (5.34). Как известно, для решения интегральных уравнений Фредгольма второго рода, включая вычисление спектральных характеристик и квадратур, имеется целый ряд устойчивых алгоритмов. Наряду с руководством, которое указано в п.4 под №5, они приведены в [12, 13] и целом ряде других изданий. При этом освещаются, вообще говоря, созвучные подходы.

Можно выделить алгоритм численной реализации резольвенты С.Г.Михлина [14, п.12], базирующийся на конечно-элементной аппроксимации ядра интегрального уравнения. Особенно интересным представляется метод Г.Н.Положего [15], преобразующий интегральное уравнение Фредгольма второго рода так, что его решение, вне зависимости от значения параметра, достигается с помощью простых итераций. В этой связи установлено начальное приближение и используется второе итерированное ядро.

Для сходимости в среднем простых итераций к решению уравнения (5.34) требуется, чтобы

                                                                                            (5.38)
где

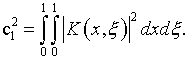
Если же

 
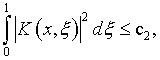
где  – постоянная, и выполнено условие (5.38), то соответствующий ряд Неймана  сходится абсолютно и равномерно [16].

Заметим, что возможность варьирования параметром  создает дополнительный резерв повышения эффективности процедуры численной реализации.

Вместо (4.13) в выкладках настоящего подраздела могло бы использоваться и другое ядро  Вместе с тем, многочисленные достоинства ядра Пуассона, о которых говорилось выше, делают такую замену совершенно излишней. Действительно, если  удовлетворяет условиям теоремы Мерсера, отказываться от чего не имеет ни какого смысла, то [2, с.166]:

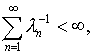
и в качестве характеристических чисел альтернативного ядра можно было бы принять, например, величины, обратные членам сходящейся арифметической или же геометрической прогрессии. Получить от этого какую-либо выгоду весьма проблематично, наряду с чем, некоторые из имеющихся преимуществ могут быть утеряны.

Обсудим вопрос об адаптации уравнения (4.1) к пространству  (определяемому условием (5.22)), который неоднократно затрагивался выше. Итак,  – область значений оператора  не является замкнутой, чем обуславливаются все сложности определения функции  удовлетворяющей уравнению (4.1), в постановке решения интегрального уравнения Фредгольма первого рода.

Что касается (5.32), то здесь отмеченное обстоятельство не имеет значения, поскольку, обращая оператор  получаем интегральное уравнение Фредгольма второго рода, а именно (5.34). Вместе с тем, построение уравнения (5.32) осуществляет весьма интересный субъект, а именно (4.7). Это интегральное уравнение Фредгольма как первого, так и второго рода, относительно функций соответственно  и

Однако в первом из указанных качеств оно принципиально отличается от (4.1) тем, что свободный член  определяемый выражением (4.8), не принимая конкретных значений, зависит от искомой функции  Поэтому, можно полагать, что

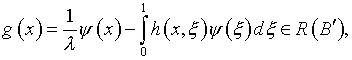
где оператор

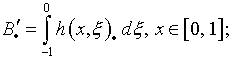
и, как представляется, элемент упомянутой выше адаптивности – налицо.

Затем, в результате распространения (4.7) на  появилось интегральное уравнение Фредгольма второго рода (4.24) относительно  см. (5.24), с функцией  представляющей его свободный член. В самом деле, зная  путем обращения оператора  можно определить функцию  а также и  Заметим, однако, – от нахождения функции  содержащейся под интегралом (4.1), задача превратилась в определение функции  которая входит явно!

Как вновь не обратиться к доводам Ж.Адамара о существовании корректных постановок физически содержательных задач, а также неоднократно звучавшему в тексте предложению рассматривать (4.1) как правило, по которому осуществляется интегрирование функции ? Суть в том, что будучи подставлена в некоторое интегральное уравнение Фредгольма второго рода, эта функция порождает соответствующий свободный член. Следовательно, задача сводится к процедуре его определения, которая имеет мощный ресурс, а именно возможность произвольно выбирать (на самом деле, каким-то образом выстраивать) ядро интегрального уравнения.

Можно предположить, что здесь реализован лишь один из ряда существующих подходов обозначенной направленности. Если имеется столь благоприятный объект как интегральное уравнение Фредгольма второго рода и свободный член, при котором ему удовлетворяет функция  объективно существует, – то нет альтернативы корректной постановке задач математической физики!

Возвращаясь к алгоритму, проследим как конкретно такая постановка осуществлялась. Итак, найдена функция  – часть решения (5.34), обусловленная  Свойства используемого при этом уравнения (4.40), в вычислительном отношении, – превосходные.

Исключение из (5.33) компоненты решения, зависящей от  привело к соотношению (5.2); с его помощью посредством резольвенты определена функция  Она и есть – свободный член, к определению которого сведена задача. В этой связи, учитывая также (5.37), еще раз обратим внимание на (4.28), (4.30) – представления  – соответственно «интегральное» и с функцией  входящей явно. Их варьирование при проведении преобразований в интересах реализации устойчивой процедуры вычисления функции  явилось одним из определяющих факторов.

Таким образом, задача (4.1) превратилась в решение интегрального уравнения Фредгольма второго рода (5.34), вычитая из которого (4.40), с учетом (4.39), получаем

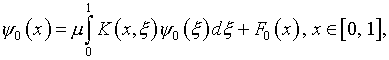                             (5.39)
где

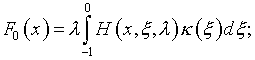
функция  определяется выражениями (5.37) и (5.18). Действительно,  – та же функция, которая содержится в (4.36). Это следует из уравнений (4.34), (4.35), а также представлений решения (4.28) и (4.31), то есть

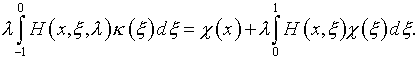
Итак, функцию  можно определить, сложив решения уравнений (4.40) и (5.39):

После нахождения функции  задачу можно решать также, используя подстановку выражения (5.26) в (4.28). При этом функция  удовлетворяет интегральному уравнению Фредгольма второго рода

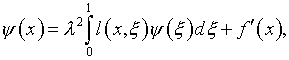                                                 (5.40)                                                                                                                                                       
где

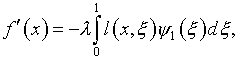
см. также (4.55).

Соответственно решение (5.40) выражается через резольвенту (4.56):

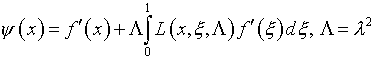
и, как можно заметить, в этом случае численно решается лишь одно интегральное уравнение Фредгольма второго рода – (4.40). Затем производятся исключительно процедуры интегрирования.

Уравнения (4.40) и (5.39), или же (4.40), с использованием, (5.40), данные которых оговорены выше, олицетворяют собой задачу (4.1) в ее корректной постановке!

Если сопоставлять алгоритмы пп. 4.4, 4.6 и настоящего подраздела, то, конечно, второй из них более формализован, что может оказаться в некотором смысле предпочтительным.