1.2. Гипотеза Ж.Адамара
и некорректность “реальных” задач
Итак, Ж.Адамар и другие выдающиеся ученые полагали,
что любая физически интерпретируемая задача может быть корректно
поставлена, однако в современных изданиях доминирует совершенно
противоположная точка зрения. В самом деле, заметно большая часть
практически значимых задач, которые в них рассматриваются, -
некорректны. Однако адекватна ли собственно методология математической
постановки этих задач, а соответственно и результаты ее преломления
к реалиям?
Здесь мы не станем углубляться в нечто вроде общих
принципов построения дифференциальных уравнений и, вообще говоря,
вначале вопрос целесообразно сузить: из каких соображений судят
о том, что некорректно поставленная задача адекватно описывает наблюдаемое
явление, или же потенциально реалистичный процесс? В этой связи
обратимся к процедуре решения интегрального уравнения Фредгольма
первого рода
 (1.6)
(1.6)
– классической некорректной задаче: ядро 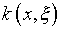 и свободный член
и свободный член 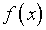 – заданы; функция
– заданы; функция  – подлежит восстановлению.
– подлежит восстановлению.
Пусть, для определенности, ядро k симметрично
и замкнуто, то есть  и его собственные функции
и его собственные функции  ,
представляющие собой нетривиальные решения интегрального уравнения
,
представляющие собой нетривиальные решения интегрального уравнения

с характеристическими числами  образуют
полную в
образуют
полную в 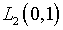 ортогональную систему элементов. Кроме того, функция
ортогональную систему элементов. Кроме того, функция  .
В этом случае по теореме Пикара решение уравнения (1.6) существует
и единственно при условии (см., например, [18])
.
В этом случае по теореме Пикара решение уравнения (1.6) существует
и единственно при условии (см., например, [18])
 (1.7)
(1.7)
Если предположить, что все перечисленные требования
выполнены, остается третье условие корректности, которому, как известно
[19, c.69], уравнение (1.6) заведомо не удовлетворяет. Многочисленные
руководства наглядно иллюстрируют неадекватно сильное влияние на
решение малых возмущений данных задачи, в первую очередь  .
Зачастую эта функция определяется экспериментально и рассогласована
с ядром
.
Зачастую эта функция определяется экспериментально и рассогласована
с ядром 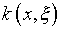 по гладкости, а, следовательно, уравнение (1.6), строго говоря,
вообще утрачивает смысл. Вместе с тем возможность эквивалентного
описания реальных задач посредством интегральных уравнений первого
рода в настоящее время признана несомненной, о чем свидетельствует
их колоссальный перечень [6].
по гладкости, а, следовательно, уравнение (1.6), строго говоря,
вообще утрачивает смысл. Вместе с тем возможность эквивалентного
описания реальных задач посредством интегральных уравнений первого
рода в настоящее время признана несомненной, о чем свидетельствует
их колоссальный перечень [6].
Конкретизируем уравнение (1.6):
 (1.8)
(1.8)
где m – целое положительное число.
При этом  . Использование теоремы Мерсера [18], согласно которой
. Использование теоремы Мерсера [18], согласно которой
 ,
,
и представление  в виде ряда по
в виде ряда по  с неопределенными коэффициентами позволяет найти решение уравнения
(1.6)
с неопределенными коэффициентами позволяет найти решение уравнения
(1.6)
 (1.9)
(1.9)
Но столь простой вычислительная процедура оказалась
вследствие специального выбора данных задачи. В противном случае,
или же при решении уравнения (1.6) с ядром и свободным членом (1.8)
одним из численных методов, сложность реализации достаточно высокого
приближения практически идентична наиболее общей ситуации, характеризующейся
погрешностью определения и
и 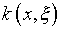 *.
*.
| * Здесь сложность подразумевает плохую обусловленность систем
линейных алгебраических уравнений, получаемых в результате некоторой
дискретизации. Существующие методы ее преодоления отражены в
п.2. |
Суть в том, что даже при объективной совместимости
данных некорректность уравнения (1.6) обуславливается погрешностью
аппроксимации f и k, а также округлением значащих
цифр ЭВМ.
Основополагающий фактор некорректности уравнения
(1.6) вытекает из сопоставления свободного члена (1.8) с решением
(1.9). В самом деле, наращивая m, функцию  можно сделать как угодно малой без изменения амплитудного значения
можно сделать как угодно малой без изменения амплитудного значения
 .
Соответственно та или иная погрешность вычислительных операций с
.
Соответственно та или иная погрешность вычислительных операций с
 проецируется на
проецируется на  ,
имея множитель m2. Механизм этого явления, связанный
со сглаживанием информации об искомой функции процедурой интегрирования,
будет неоднократно затронут в ходе последующего изложения.
,
имея множитель m2. Механизм этого явления, связанный
со сглаживанием информации об искомой функции процедурой интегрирования,
будет неоднократно затронут в ходе последующего изложения.
Однако вернемся к сформулированному вопросу о
сопряжении некорректной постановки с реальностью и в этой связи
обратим внимание на следующее обстоятельство. Рассматривая (1.6)
в качестве интегрального уравнения Фредгольма первого рода (функция
y подлежит определению), мы подразумеваем решение обратной
задачи (О). Но (1.6) можно использовать и для решения соответствующей
прямой задачи (П): вычисление функции  по данным
по данным 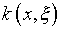 и
и  .
Эта процедура корректна, а значит радикально проще задачи О. Достаточно
заметить, что отсутствует принципиальное различие между сугубо численной
реализацией и интегрированием выражений (1.8), (1.9) в аналитическом
виде.
.
Эта процедура корректна, а значит радикально проще задачи О. Достаточно
заметить, что отсутствует принципиальное различие между сугубо численной
реализацией и интегрированием выражений (1.8), (1.9) в аналитическом
виде.
И здесь хотелось бы привлечь внимание к моменту,
который представляется весьма существенным. Задача П, как правило,
прозрачна – в ее категориях мы вполне естественно моделируем происходящие
процессы и явления наглядными, что важно подчеркнуть, средствами
линейной суперпозиции. Соответственно если, например, 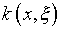 – характеристика среды, а
– характеристика среды, а  – интенсивность внешнего воздействия, результат события в той или
иной предметной области остается лишь элементарно просуммировать.
– интенсивность внешнего воздействия, результат события в той или
иной предметной области остается лишь элементарно просуммировать.
Ситуация с задачей О – диаметрально противоположна.
Едва ли представляется возможным указать реальный процесс (явление),
для которого ее удалось бы формулировать математически непосредственно
из соображений предметной области. Иначе говоря, вне привязки к
задаче П, наряду с чем общепринятой является трансформация последней
в задачу О посредством механического переименования известных и
неизвестных компонентов.
По нашему мнению, глубоко порочна методология,
в рамках которой на основании вполне доброкачественной информации
о конкретной задаче П делается утверждение об адекватности реалиям
задачи О, полученной с помощью указанного переименования компонентов.
Соответственно неосновательными следует считать суждения специалистов,
отвергающих гипотезу Ж.Адамара о существовании корректных постановок
задач математической физики.
Обратимся к задаче П, описывающей некоторый реальный процесс (1.6).
Для него, конечно же, имеет смысл определение  по данным
по данным 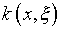 и
и 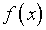 ,
то есть, постановка и решение соответствующей обратной задачи, которую
обозначим через О¢. Предположим,
что в рассматриваемом случае гипотеза Ж.Адамара верна и, следовательно,
задача О¢ – корректна. Но задача
О – решение интегрального уравнения Фредгольма первого рода (1.6)
некорректна по определению.
,
то есть, постановка и решение соответствующей обратной задачи, которую
обозначим через О¢. Предположим,
что в рассматриваемом случае гипотеза Ж.Адамара верна и, следовательно,
задача О¢ – корректна. Но задача
О – решение интегрального уравнения Фредгольма первого рода (1.6)
некорректна по определению.
Вывод очевиден: математические постановки задач О и О¢
– нетождественны. Следовательно, постановка задачи О¢
не может ограничиваться лишь переадресацией статуса неизвестной
между функциями f и y в задаче П. Заметим в этой
связи, что конструктивная методология корректной постановки задачи
О¢ является основным предметом,
а также главной целью настоящего исследования.
Приведенные аргументы представляются достаточно вескими однако на
данном этапе изложения мы не можем как доказать правомерность гипотезы
Ж.Адамара в общем случае, так и проиллюстрировать ее конструктивизм
применительно к отдельным классам задач. Следует также учесть, что,
используя специальные приемы, решение некорректной задачи О зачастую
удается получать с точностью, которая считается практически приемлемой.
В связи с этим возникает вопрос: следует ли стремиться к корректной
постановке О¢, если алгоритм вычисления
функции  в постановке задачи О так или иначе осуществляет ее регуляризацию?
Имеется в виду хорошо известная деформация постановки О с использованием
малого параметра, сообщающая ей свойства корректной разрешимости.
в постановке задачи О так или иначе осуществляет ее регуляризацию?
Имеется в виду хорошо известная деформация постановки О с использованием
малого параметра, сообщающая ей свойства корректной разрешимости.
Итак, способен ли алгоритм в полной мере, включая
эффективность численной реализации, нивелировать принципиальные
осложнения, заложенные некорректностью задачи О вида (1.6)? Понятно,
что ответ может быть только отрицательным – в противном случае утратила
бы смысл прочно устоявшаяся дифференциация задач на корректно и
некорректно поставленные. Более того, обозначенное различие является
исключительно существенным, поскольку корректность постановки –
критерий качественного уровня, что же касается эффективности метода
решения интегрального уравнения Фредгольма первого рода, то его
можно измерять лишь в количественных показателях паллиативного свойства.
Последнее обуславливается непосредственной взаимозависимостью между
глубиной регуляризации и деформацией (искажением) задачи О.
Однако в чем собственно может выражаться разночтение постановок
О и О¢? За ответом на этот вопрос
основополагающая концепция предлагаемого подхода. В настоящем заметим
лишь, что трансформация постановки О к О¢
будет иметь преимущественно качественный характер и реализоваться
посредством нулевого в  возмущения уравнения (1.6), моделирующего феномен сглаживания информации.
возмущения уравнения (1.6), моделирующего феномен сглаживания информации.

