| |
|
|
|
7.1. Начально-краевая задача для уравнения Кортевега-де Вриза
7.2. Краевая задача для существенно нелинейного дифференциального уравнения
7.3. Нелинейность граничного условия
7.4. Малый параметр при старшей производной дифференциального уравнения
7.5. Уравнение смешанного типа
7.6. Обратная задача о восстановлении коэффициента дифференциального уравнения
7.7. Задача стефановского типа
Предположим,
что в пространстве 
существует
и единственно решение задачи:
 |
(7.1) |
 |
(7.2) |
при данных функциях 
Общей теории, которая позволяла бы априорно судить о разрешимости подобных задач, не существует. Основным средством уточнения математических моделей служат результаты численного эксперимента, а также решения специальным образом упрощенных уравнений вблизи границ [1, п.10].*
Используя процедуру предыдущего раздела, задачу (7.1), (7.2) можно свести к нелинейному интегральному уравнению первого рода относительно
откуда
 |
(7.3) |
где определяемые из граничных условий функции
Их подстановка в (7.3) приводит к выражению
 |
(7.4) |
Уравнение (7.1) представим в виде
 |
(7.5) |
подстановка выражения (7.4)
в правую часть (7.5) и
интегрирование от 
до 
с учетом начального условия (7.2)
позволяют определить
 |
(7.6) |
Исключение 
из выражений (7.4), (7.6)
приводит к уравнению вида
  |
(7.7) |
где 
– нелинейный
интегральный оператор; 
– функция,
зависящая от данных задачи.
Для определения
функции 
может быть использован алгоритм п.6.4 (переменная 
заменяется на 
). При этом она будет удовлетворять нелинейному интегральному уравнению второго
рода. На основании принципа сжатых отображений, при достаточно малом по модулю
значении параметра 
его решение находится с помощью простых итераций [2].
Имеется в виду нелинейность вхождения старших производных. В качестве примера рассмотрим уравнение Монжа-Ампера
 |
(7.8) |
где 
и 
в общем случае зависят от переменных 
искомой функции 
и ее первых производных 
[3].
Предположим,
что 
и
 |
(7.9) |
решение задачи в 
существует
и единственно. Если обозначить
то с учетом (7.9)
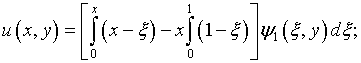
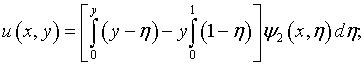
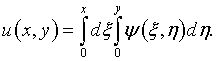
В результате
подстановки этих выражений в (7.8)
и исключения функции 
задача сводится к системе уравнений:
 |
(7.10) |
 |
(7.11) |
 |
(7.12) |
Двукратное дифференцирование
уравнений (7.11), (7.12)
соответственно по 
и
дает:
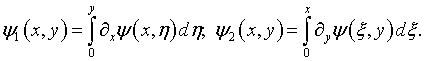
Уравнение (7.10) приобретает вид
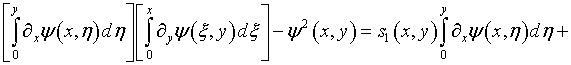
и после интегрирования в пределах 
и
приводится
к следующему –
 |
(7.13) |
где – соответствующий
нелинейный интегральный оператор;
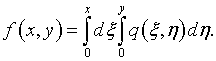
При
этом предполагается ограниченность производных 
О
возможном пути решения этого уравнения сказано в п.7.1.
Задача об излучении неограниченной пластины с одной теплоизолированной поверхностью в среду, абсолютная температура которой равна нулю, формулируется так [4]:
 |
(7.14) |
 |
(7.15) |
Здесь
–
перепад температур; 
–
данная функция; 
–
коэффициент температуропроводности; 
где
и
–
коэффициенты соответственно теплопроводности и теплопередачи; 
–
параметр.
Обозначим
 |
(7.16) |
откуда
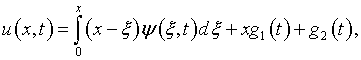
где 
–
функции интегрирования.
Из граничных условий (7.15)
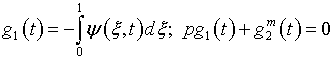
и соответственно
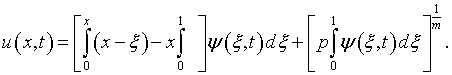
Используя (7.14), (7.16), с учетом начального условия (7.15) получаем
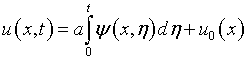
и задача сводится к решению нелинейного интегрального уравнению первого рода (7.7), в котором
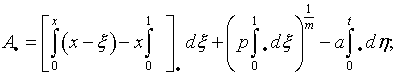
Общие соображения проиллюстрируем задачей о распространении тепла, обусловленном процессами теплопроводности и конвекции (соответственно первое и второе слагаемое правой части уравнения) [5]:
 |
(7.17) |
Здесь
–
постоянная; 
– малый
параметр,
 |
(7.18) |
где 
–
данная -функция.
Из обозначения (7.16) с учетом граничных условий (7.18) следует
 |
(7.19) |
Интегрирование
уравнения (7.17) в пределах
с использованием (7.19)
и начального условия (7.18)
дает
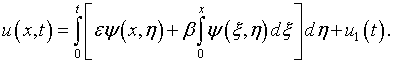
Исключение из
этих выражений функции
приводит к уравнению (7.7),
в котором
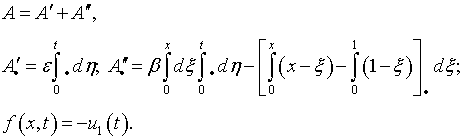
Алгоритм п.6.4 позволяет свести задачу к решению интегрального уравнения Фредгольма второго рода, имеющего вид:
 |
(7.20) |
где 
и
–
соответствующие интегральные операторы; 
В результате разложения [6]
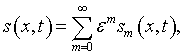
возникает последовательность рекуррентных соотношений
…
которые представляют собой канонические интегральные уравнения Фредгольма второго рода.
Из этого следует, что предлагаемый подход эффективен в задачах математической физики с сингулярным возмущением, численная реализация которых, зачастую, встречает существенные осложнения (см., в частности, [7]). Действительно, сингулярное возмущение (7.17) оказалось возможным перевести в регулярное – (7.20), вследствие чего задача значительно упростилась.*
Краевые задачи для таких уравнений характеризуются сложностью исследования вопросов существования и единственности решений [8]. Из-за этого их приходится рассматривать в областях достаточно специального вида, что сужает круг практических приложений.
Абстрагируясь от данной проблематики, в целях исключительно иллюстрации процедуры преобразований, обратимся к известному уравнению Трикоми
 |
(7.21) |
которое является гиперболическим и эллиптическим, соответственно при 
и
Используем,
например, следующие граничные условия
 |
(7.22) |
где функция 
такова,
что 
Из обозначения
 |
(7.23) |
с учетом (7.22)
двукратное интегрирование уравнения (7.21)
в пределах 
с учетом (7.23) и (7.22),
приводит к выражению
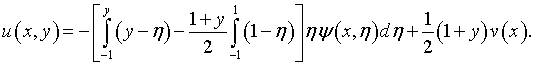
Задача сводится
к интегральному уравнению Фредгольма первого рода (7.13)
в области 
которое имеет оператор
и свободный член
Обратим внимание,
естественно выполняется так называемое условие «склеивания» на линии параболического
вырождения 
которое предъявляется к решению уравнения (7.21)
[8, c.27]:
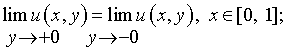
Как и в предыдущем подразделе, данное обстоятельство обуславливается переведением возмущения задачи от главного члена, описывающего ее оператора, – к подчиненному.
Малые колебания в поперечном направлении растянутой струны переменной плотности описываются уравнением
 |
(7.24) |
Здесь
–
безразмерные координаты;
где 
–
натяжение; 
–
плотность материала; 
–
длина струны; 
– временной
интервал.
Предполагается,
что края струны закреплены и ее плотность, а также колебания симметричны относительно
координаты 
При
этом граничные условия имеют вид
 |
(7.25) |
используем также начальные условия:
 |
(7.26) |
Требуется определить
коэффициент 
на основании (7.24) –
(7.26) при данных 
и дополнительной информации о колебаниях среднего сечения струны
 |
(7.27) |
условия существования и единственности решения сформулированной задачи (см. [9, п.4]) считаем выполненными.
Аналогично неоднократно проделанному выше, с использованием обозначения (7.16) и (7.24) – (7.26), находим
 |
(7.28) |
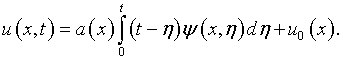
Исключая 
получаем уравнение вида (7.7).
Подстановка (7.28) в (7.27)
приводит к интегральному уравнению
где
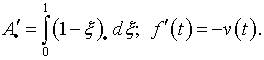
Процедуру
решения сформированной таким образом системы уравнений можно представить в контексте
дополнения алгоритма п.6.4 итерациями с участием функции 
Рассмотрим классическую модель [10]:
 |
(7.29) |
 |
(7.30) |
На движущейся границе, которая представляет собой раздел фаз, задается дополнительное условие
 |
(7.31) |
где 
–
постоянная; может
принимать как положительное, так и отрицательное значение; 
Таким
образом, данные задачи: 
и
функции
и
подлежат
определению.
В (7.29) – (7.31) произведем неортогональное отображение
 |
(7.32) |
на каноническую область 
Получаем
 |
(7.33) |
 |
(7.34) |
 |
(7.35) |
Аналогично предыдущему, из обозначения
условий (7.34) и уравнения (7.33) следует
 |
(7.36) |
 |
(7.37) |
Подстановка выражения (7.36) в (7.35) дает
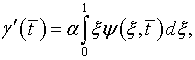
откуда
 |
(7.38) |
Соответственно в выражении (7.37)
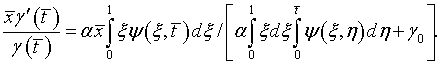
Исключение 
из (7.36), (7.37)
приводит к интегральному уравнению первого рода (7.7).
После определения, удовлетворяющей ему функции 
последнюю следует аппроксимировать аналитической зависимостью по 
для проведения обратной замены переменных. При этом граница раздела 
будет находиться из нелинейного интегрального уравнения (7.38).
Далее, по формуле (7.36),
с учетом (7.32), можно
вычислить функцию 
