| |
|
|
|
6.1. Обыкновенные дифференциальные уравнения
6.2. Иллюстрация процедуры сведения
6.3. Универсальность и аналогичные подходы
6.4. Сопряжение с алгоритмом п.5.4
6.5. Проверка краевых задач на разрешимость
Пусть, например:
 |
(6.1) |
 |
(6.2) |
где 
и
– данные
-функции.
Из обозначения
 |
(6.3) |
следует
 |
(6.4) |
 |
(6.5) |
где 
,
–
постоянные интегрирования.
Подстановка выражений (6.3) и (6.5) в (6.1) приводит к интегральному уравнению Вольтерра второго рода
 |
(6.6) |
решение которого имеет вид:
 |
(6.7) |
где 
–
резольвента ядра 
Из граничных
условий (6.2) с учетом
(6.4), (6.5)
и (6.7): 
 |
(6.8) |
Можно поступить
иначе, а именно, подставив выражения (6.4),
(6.5) в (6.2),
найти
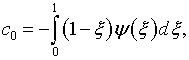
в результате чего
 |
(6.9) |
В отличие от (6.6), задача сводится к интегральному уравнению Фредгольма второго рода
 |
(6.10) |
решение которого
 |
(6.11) |
где
– резольвента ядра*
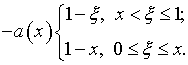
Подстановка выражения (6.7), с учетом (6.8), в (6.5), или (6.11) – в (6.9), позволяет найти решение задачи (6.1), (6.2). Заметим, что рассмотренный прием практически индифферентен к порядку дифференциального уравнения, виду граничных, или же начальных условий и данным задачи.
Подобные преобразования традиционно освещаются в курсах по теории интегральных уравнений (см., например, [1, 2]). Вместе с тем при решении прикладных задач, что можно охарактеризовать как своеобразный парадокс, построение интегральных уравнений второго рода относительно старшей производной не получило широкого распространения. И это, несмотря на весьма активные попытки популяризации данного подхода, среди которых можно выделить работы Ш.Е.Микеладзе, И.А.Биргера, А.Н.Голубенцева [3, 4, 5].
Видимо, причиной такого положения явились, с одной стороны, несовершенство технических средств численной реализации квадратурных формул в период, предшествовавший масштабной компьютеризации; с другой – недостаточная популярность аппарата теории интегральных уравнений в среде прикладников.
И вместе с тем вот, что говорит Г.Виарда [6, с.5]: «… интегральное уравнение заменяет собой соответствующее дифференциальное уравнение вместе с его граничными условиями, которые, если только речь идет о вполне определенном физическом явлении, необходимо появляются при всяком дифференциальном уравнении. Интегральное уравнение, содержит в себе уже все элементы, определяющие физическую задачу. Следующее преимущество интегральных уравнений состоит в том, что в большинстве случаев мы приходим к уравнениям одного и того же типа …, в то время как типы дифференциальных уравнений, даже в очень родственных задачах, часто оказываются весьма различными».
Обратимся к задаче изгиба равномерной нагрузкой мембраны, растянутой по контуру:
 |
(6.12) |
 |
(6.13) |
 |
(6.14) |
Из обозначения
 |
(6.15) |
следует
 |
(6.16) |
где 
–
функции интегрирования.
С учетом (6.15) уравнение (6.12) принимает вид
и соответственно
 |
(6.17) |
где 
–
также функции интегрирования.
Подстановка
выражений (6.16), (6.17)
в граничные условия соответственно (6.13)
и (6.14) позволяет определить
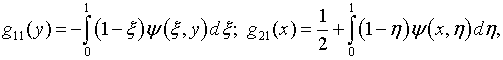
в результате чего выражения (6.16) и (6.17) приобретают вид соответственно:
 |
(6.18) |
 |
(6.19) |
Исключая
из них 
получаем
интегральное уравнение Фредгольма первого рода:
 |
(6.20) |
Итак, принципиальное отличие от одномерного случая состоит в том, что задача
(6.12) – (6.14)
свелась к некорректно поставленной. Однако в настоящем нас будет интересовать
не определение функции 
удовлетворяющей уравнению (6.20)
(заметим лишь, что алгоритмы пп. 4.4, 4.6 и 5.3 на него распространяются), а
собственно универсальность используемой процедуры преобразований.
В самом деле,
пусть область определения задачи отлична от канонической и, например, второе
условие (6.13) имеет вид
где 
– некоторая однозначная функция. При этом вместо (6.18)
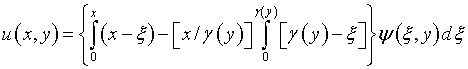
и, с вычислительной точки зрения, отличительные моменты отсутствуют. Для
перехода к обычной операции вычисления интеграла в прямоугольной области достаточно
воспользоваться неортогональным отображением вида 
Нетрудно заметить,
что каждое из выражений (6.18),
(6.19) тождественно удовлетворяет
паре граничных условий, соответственно (6.13)
и (6.14). Остальные –
выполняются приближенно, в зависимости от точности вычисления 
Вместе с тем, решение можно представить в виде, тождественно удовлетворяющем
как условиям (6.13), так
и (6.14):
Здесь функции
определяются по формулам соответственно (6.18)
и (6.19).
Норма
невязки значений 
или
позволяет
оценить погрешность приближенного решения
Однако, если вместо (6.13) были бы поставлены условия
вытекающее из (6.15) выражение производной
для их удовлетворения не подходит.
Тем не менее, данное осложнение легко преодолевается с помощью, например, соотношения
где 
– постоянная,
позволяющего сохранить присутствие обоих функций интегрирования 
Обратимся к эквивалентной формулировке задачи (6.12) – (6.14):
 |
(6.21) |
 |
(6.22) |
с использованием представлений решения вида
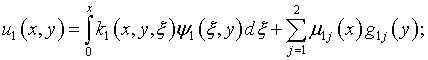
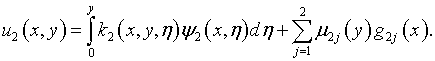
Предполагается, что ядра, удовлетворяющие условиям:
 |
(6.23) |
– заданы; 
–
также данные функции; 
–
подлежат определению из граничных условий, аналогично изложенному выше.
Примем 
В этом случае с учетом условий (6.22):
 |
(6.24) |
 |
(6.25) |
и соответственно
 |
(6.26) |
 |
(6.27) |
Пусть в дополнение
условий (6.23), 
и 
являются L2-ядрами. При этом (6.26),
(6.27) представляют собой
интегральные уравнения Вольтерра второго рода относительно функций 
решения которых в соответствии с положениями общей теории существуют и единственны.
Таким образом, представления (6.24)
и (6.25) отвечают физическому
содержанию задачи (6.21),
(6.22).
В (6.23) можно принять
где
используя эти выражения для преломления априорной информации о решении с
целью сглаживания искомых функций 
и
в целом – упрощения процедуры вычислений. Понятно, что отмеченный момент актуален
для более сложных задач с различного рода особенностями поведения решений и здесь
он лишь обозначен.
Подстановка 
и 
из (6.26), (6.27)
в (6.21) приводит к системе
интегральных уравнений
 |
(6.28) |
где
 |
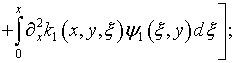
(6.29) |
Из уравнения (6.28)
 |
(6.30) |
где 
–
резольвента ядра 
Подстановка
выражения (6.30) в (6.29)
позволяет получить интегральное уравнение Фредгольма первого рода относительно
функции 
Очевидно, приведенная схема преобразований более громоздка по сравнению с базирующейся
на формулировке той же задачи в обычной интерпретации (6.12)
– (6.14). Вместе с тем,
в ней можно усмотреть итерационные начала, которые обуславливаются тем, что
(6.28) представляет собой
интегральное уравнение Вольтера второго рода относительно функций как 
так и 
Процедура преобразований подходит также и для дифференциальных уравнений других типов, в подтверждение чего рассмотрим задачу теплопроводности:
 |
(6.31) |
 |
(6.32) |
Из 
уравнения (6.31) и условий
(6.32) следует:
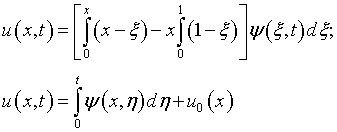
и соответственно
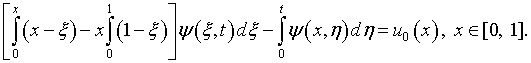
Для аналогичного преобразования задачи изгиба прямоугольной пластины переменной жесткости D, защемленной вдоль контура [7]:
 |
(6.33) |
 |
(6.34) |
где 
–
коэффициент Пуассона; 
–
интенсивность поперечной нагрузки, можно принять
 |
(6.35) |
Здесь
функции
предназначены для удовлетворения условий (6.34)
при 
и 
Второе представление решения задачи через 
определяется путем подстановки (6.35)
в уравнение (6.33) и четырехкратного
интегрирования по переменной 
Возникающие при этом функции 
позволяют удовлетворить условия (6.34)
при 
и 
после чего 
из представлений решения исключается.
Заметим,
что, с помощью 
могут
быть удовлетворены условия в отдельных точках внутри рассматриваемой области,
например, 
Процедура
преобразований, распространяется на собственно смешанные граничные условия (изменение
типа вдоль стороны) и случай сопряжения пластин. По аналогичной схеме к интегральным
уравнениям Фредгольма первого рода могут приводиться также и трехмерные задачи
математической физики.
Итак, вполне элементарный прием, или же способ сведения линейных краевых и начально-краевых задач к интегральным уравнениям Фредгольма первого рода весьма универсален с точки зрения своей реализации в части следующих аспектов:
- порядок, и структура дифференциальных операторов;
- вид граничных условий;
- наличие переменных коэффициентов;
- форма области определения;
- размерность задачи.
При этом вся информация о конкретно рассматриваемой задаче переносится в функциональное уравнение, решение которого не требуется подчинять каким-либо условиям на контуре области, что представляет существенное преимущество. Так, его можно искать в виде ряда по системе элементов, наиболее удобных с точки зрения процедуры численной реализации.
Другое дело, что получаемая в результате преобразований задача становится некорректной, а соответственно для ее решения необходимо использовать специальные методы. Вместе с тем, в приложениях может оказаться приемлемой аппроксимация решения такой задачи рядом, число членов которого не так велико, чтобы негативно влиять на устойчивость реализации вычислительных алгоритмов. Исходя из этого, трудно объяснимым представляется отсутствие интереса к применению продемонстрированной процедуры преобразований, в особенности – до появления возможностей использования универсальных методов дискретизации.
Следует отметить, что в специальной литературе не прозвучал тезис о существовании формализованного приема сведения практически произвольных краевых и начально-краевых задач к интегральным уравнениям Фредгольма первого рода. Наряду с этим, имеется целый ряд примеров применения подобных преобразований в ситуациях сравнительно частного характера. Как правило, им придавалась физическая интерпретация, в значительной мере скрадывавшая масштабность упомянутого приема.
Так, Ю.В.Репман
использовал в качестве функции, близкой по смыслу
краевые усилия пластинки канонического очертания, позволяющие удовлетворять
условиям на внутреннем контуре сложной конфигурации [8].
Л.А.Розин разработал метод расчленения, сводящий задачи расчета оболочек к
системам интегральных уравнений Фредгольма первого рода относительно усилий
взаимодействия выделяемых стержней [9,
п.9]. В ряде публикаций отмечены преимущества аппроксимации старших производных
дифференциальных уравнений по одной из переменных, после чего остается воспользоваться
операциями интегрирования, которые, если их сравнивать с численным дифференцированием,
являются гораздо более точными. Фактический переход при этом к некорректным
задачам, как правило, не комментировался, см., в частности, [10].
Некоторые задачи для дифференциальных уравнений в частных производных и, например, следующего:
где 
и 
– данные функции переменных 
и 
сводятся к интегральным уравнениям Вольтерра или Фредгольма второго рода относительно
старшей производной 
Соответствующие исследования выполнены Г.Мюнтцем [11]
и, в этой связи, значительный интерес представляет установленная им безуспешность
попыток распространения аналогичных преобразований на случай простейшего уравнения
эллиптического типа.
Интегральное уравнение Фредгольма первого рода, возникающее в случае приведения к нему двумерных краевых (начально-краевых) задач, можно представить в виде:
 |
(6.36) |
где 
и
–
данные функции; 
– необходимо
определить.
В предположении о том, что функция, удовлетворяющая уравнению (6.36) существует и единственна, она определяется как
 |
(6.37) |
где 
и
–
решения двумерного интегрального уравнения Фредгольма второго рода
 |
(6.38) |
при свободном члене соответственно:
 |
(6.39) |
 |
(6.40) |
В уравнении (6.38) ядра:
 |
(6.41) |
Здесь и выше
 |
(6.42) |
где параметр 
 |
(6.43) |
В
этом выражении 
 |
(6.44) |
где
 |
(6.45) |
 |
(6.46) |
Параметр
:
параметр
где 
–
характеристические числа однородного уравнения
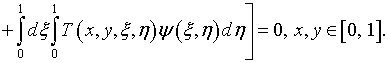
После
выбора значений 
и 
(которые
затем могут, исходя из различных соображений, корректироваться) последовательность
вычислительных процедур состоит в определении:
- ядер
уравнения (6.38) 
и 
– по формулам (6.41),
с использованием выражения (6.42);
- свободного
члена 
– по формуле (6.40);
- функции
– из уравнения (6.38),
с 
- функции
– по формуле (6.44), с
использованием выражения (6.45);
- функции
– по формуле (6.43), с
использованием выражения (6.46);
- свободного
члена 
– по формуле (6.39);
- функции
– из уравнения (6.38),
с 
- искомой
функции
– по формуле (6.37).
Как
можно заметить, алгоритм п.5.4 переносится на решение двумерного интегрального
уравнения Фредгольма первого рода без сколько-нибудь существенных изменений. Переменная
при
этом выступает в качестве параметра.
Выше предполагалось
существование и единственность функции 
удовлетворяющей интегральному уравнению Фредгольма первого рода (6.36)
в пространстве 
Тем не менее, формально используя расчетные соотношения п.6.4, можно «найти»
и в случаях, когда уравнение (6.36)
неразрешимо, или же имеет множество решений. В первом из них – функция
будучи подставлена в (6.36),
не сможет удовлетворить этому уравнению.
Действительно,
полученное таким образом решение не имеет смысла, поскольку построение алгоритма
(см. п.5.3) основывалось на том, что удовлетворяющая уравнению (4.1)
функция существует и, более того, свободный член
трактовался как результат предварительно произведенного интегрирования. Но есть
и другая сторона вопроса: если найденная с помощью алгоритма п.6.4 функция
при ее подстановке не удовлетворяет (6.36),
то значит это уравнение – неразрешимо.
Что же, однако, мы имеем? Неприятные свойства интегрального уравнения Фредгольма первого рода, о которых так много говорилось выше, могут быть весьма эффективно использованы в целях исследования краевых (начально-краевых) задач на разрешимость. В самом деле, они легко сводятся к двумерным (или большей размерности) интегральным уравнениям Фредгольма первого рода, чему был посвящен материал п.6.2. Остается, следовательно, после реализации алгоритма п.6.4, проверить удовлетворяет ли полученное решение уравнению вида (6.36).
Для сравнительно
несложных задач из предыдущих подразделов такая проверка не столь актуальна,
но, кстати, адекватности задачи (6.33),
(6.34) описанию прогиба
в углах прямоугольной пластины посвящено немало исследований. Интересно другое,
заключающееся в том, что важнейшей проблемой математического моделирования является,
собственно, формулировка задач, подразумевающая построение дифференциальных,
или же интегро-дифференциальных уравнений. В этой связи интегральное уравнение
Фредгольма первого рода (после сведения к нему так, или иначе поставленной задачи)
может служить своего рода фильтром отсеивания неудачных вариантов!
Этот короткий подраздел представляется важным. Он занял мало места, так как в значительной мере базируется на материале, который изложен выше.
