| |
|
|
|
5.1. Комментарии по материалам подразделов
5.2. Дополнительные соображения
5.3. Второй вариант решения задачи
5.4. Совокупность расчетных соотношений (к п.5.3)
В п.4.1 развиты предшествовавшие соображения о том, что восстановление
функции 
по результату интегрирования 
нельзя рассматривать в постановке решения интегрального уравнения Фредгольма
первого рода (4.1). Сформулирована
задача об определении 
по данным 
и 
с учетом неизбежно возникающей погрешности вычислений. Для этого предложено
использовать функциональную зависимость между погрешностью интегрирования –
и 
так, чтобы оказалось возможным адаптивно компенсировать малую несогласованность
между 
и значениями 
которые известны фактически, см. (4.2),
(4.3).
Далее, в п.4.2 показано, что функциональная модель погрешности вычисления
интеграла (4.1), см. п.3.5,
действительно может быть представлена выражением (4.4).
Последнее является разностью между искомой функцией
и интегралом от нее, а также еще одной неизвестной функции 
с ядром 
которое имеет вид (4.13).
При этом для выполнения (4.6)
– условия, выражающего малость 
оказалось необходимым, чтобы функция
была гармонической.
В таком предположении могут, видимо, рассматриваться задачи типа определения
параметров потока тепла (описываемого уравнением Лапласа) по результату 
его воздействия на систему с характеристикой 
Вместе с тем, желательно, чтобы функция 
удовлетворяющая уравнению (4.1),
могла быть более произвольной; в идеальном случае – принадлежащей пространству
Очевидно, упомянутая гармоничность обуславливается присутствием в выражении
параметра 
При этом использование вместо (4.13)
другого, также ограниченного ядра, практически ничего не дает, поскольку область
значений вполне непрерывного оператора не является замкнутой.*
Весьма существенный момент – произведенное в п.4.3 распространение (4.4)
при условии (4.6) на 
приведшее к уравнению (4.24).
В отличие от него, уравнение (4.25)
имеет более отвлеченную связь с задачей (4.1).
Это уравнение появилось из представлений о том, что результативности выкладок
будет способствовать использование, наряду с (4.24),
уравнения-аналога, отличающегося обращением свободного члена в нуль на другой
части интервала определения, 
Путем несложных преобразований, оказалось возможным получить ключевые в данном
случае соотношения: (4.32),
далее (4.43), (4.44),
(4.48) и итоговое – (4.50).
Уравнения (4.24) и (4.25) – весьма своеобразны. Очевидно, при вычитании
 |
(5.1) |
из уравнения (4.23), на этой части интервала определения появляется уравнение (4.25) и соответственно, с учетом также (4.44) и (4.48)
таким образом, 
(то есть, уравнения (5.1)
и (4.36) – на 
идентичны).
Одновременно происходит «перетекание» (трудно охарактеризовать эту процедуру
иначе) свободного члена уравнения (4.24)
– 
в свободный член уравнения (4.25)
– 
Действительно, вследствие (4.32),
в уравнении (4.24) на
осуществляется преобразование:
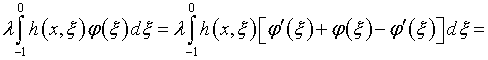
Однако, что бы ни говорилось о предпосылках построения (4.24), (4.25), как формально, так и по существу это интегральные уравнения Фредгольма второго рода, решения которых имеют вид (4.28) – (4.31). На одной части интервала определения их свободные члены содержатся в явном виде, на другой – под интегралом. Данное обстоятельство, совсем не существенное как с точки зрения положений общей теории уравнений указанного типа, так и методов их численной реализации, представляет собой очень важный фактор реализации последующих преобразований.
В п.4.3 приведена также схема построения уравнений (4.24)
и (4.25), отправляясь
от гипотетически данной функции 
Иначе говоря, структура этих уравнений не содержат противоречий.
Тривиальное, на первый взгляд, сложение
(4.1) с (4.24)
и (4.25), приведшее к
уравнениям (4.34), (4.35),
имеет весьма содержательный смысл – это встраивание модели погрешности в процедуру
определения функции
Обращаясь к п.4.4, заметим, что с помощью (4.45) и (4.48) соотношения (4.43), (4.44) преобразуются следующим образом:
 |
(5.2) |
 |
(5.3) |
(как представляется, безотносительно произведенных выше выкладок, этот результат совсем не очевиден).
Покажем как (4.34)
превращается в уравнение (4.35).* Подстановка 
из (5.3) в (4.34)
приводит к уравнениям
 |
(5.4) |
  |
(5.5) |
Из (5.3), (4.32) и (4.43) следует, что в (5.4) и (5.5) соответственно
 |
(5.6) |
 |
(5.7) |
Тождественность
(5.4), (5.5)
уравнению (4.35) очевидна
(функция 
из (5.7) исключается).
Аналогично, наоборот, (4.35)
с помощью соотношений (5.2),
(5.3) и (5.6)
превращается в уравнение (4.34).
Из (4.39) следует, что
 |
(5.8) |
то есть функция, удовлетворяющая (4.1),
является суммой решений интегральных уравнений Фредгольма второго рода (4.36)
и (4.38), обусловленных
компонентами свободного члена (4.35),
соответственно 
и 
Функция 
зависит от данных исходной задачи, представляя собой решение видоизмененного
уравнения (4.1), – искусственно
«сдвинутого» в плоскость устойчивости процедур численной реализации. Это решение
совсем другой задачи, нежели рассматриваемая и, конечно, функция
уравнению (4.1) не удовлетворяет.
В свою очередь, функция 
зависит от 
что следует из уравнений (4.36),
(4.52) и выражений (4.54),
(4.41). Сложение 
с 
в (5.8) адаптивно компенсирует
влияние упомянутого «сдвига», делая функцию
удовлетворяющей уравнению (4.1).
При этом, что следует подчеркнуть, выкладки на каждом из этапов решения:
«сдвиг»; «компенсация сдвига» осуществляются в привязке к корректно поставленной
задаче. Процедуру (5.8)
можно трактовать и как вычленение из функции
той ее части, которая препятствует удовлетворению уравнения (4.1).
Используем соотношение 
вытекающее из (5.3) и (4.39).
Соответственно 
и поскольку 
то 
или же вновь имеем (5.3).* Данное обстоятельство полностью соответствует логике «перетекания»
функций
и
одной в другую. Действительно, «отдав» 
функция 
превращается в 
и вместо
появляется 
уравнение (4.34) приобретает
вид (4.35). Обратная процедура,
то есть превращение (4.35)
в (4.34), естественно,
сопряжена с «возвращением» 
Итак, в предположении о том, что функция 
– гармоническая, задача свелась к решению уравнения (4.52).
Его свободный член зависит от функции 
которая, в свою очередь, определяется решением также интегрального уравнения
Фредгольма второго рода (4.40)
и выражением (4.41).
Отмеченный результат преобразований (их можно охарактеризовать как эквивалентные)
сопроводим интерпретацией. Есть гармоническая функция 
интегрируемая по формуле (4.1),
которая определяется выражением (4.30).
Последнее, так как 
представляет собой интегральное уравнение Фредгольма второго рода относительно
функции
При выполнении условия (4.18)
можно тем, или иным способом найти его решение – 
Подстановка 
в уравнение (4.52), безотносительно
с этой точки зрения к виду ядра 
позволяет вычислить свободный член 
То есть, уравнение (4.52)
имеет полное право на существование.
Иначе
говоря, при данном ядре
конкретно, имеющем вид (4.55),
и соответствующем значении параметра 
существует свободный член 
такой что решение интегрального уравнения Фредгольма второго рода (4.52)
– 
будучи подставлено в выражение (4.30),
позволит определить функцию 
которая удовлетворяет уравнению (4.1).
Произведенные
выкладки, собственно, состояли как в построении самого уравнения (4.52),
так и эффективном определении его свободного члена 
При этом ядро 
не зависит от данных задачи, а обуславливается исключительно интересами конструктивной
стороны преобразований. Имеется в виду возможность использования аппарата теории
интегральных уравнений Фредгольма второго рода с симметричными ядрами, проистекающая
от модели погрешности (4.4), условия (4.6),
ядра (4.13) и способа
последующего распространения задачи на
Проведению преобразований в аналитическом виде, включая
нахождение резольвенты (4.56),
существенно способствовали свойства ядра 
* В то же время, для этого вместо (4.19)
могли бы использоваться и другие сходящиеся ряды по элементам 
из (4.17).
Однако
ядру (4.13) присуще особое
качество, состоящее в том, что при 
интеграл
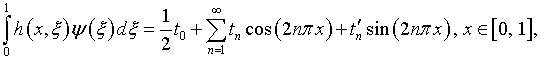
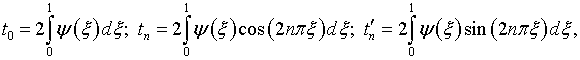
представляет собой ряд Фурье функции
по элементам (4.17). Как
известно (см., например, [2,
с. 110-116]), с помощью такого ряда можно приблизить в среднем произвольную
функцию из пространства
*
Здесь
в полной мере проявляется взаимнооднозначное, непрерывное и линейное соответствие
между пространствами 
и 
вытекающее из теоремы Рисса-Фишера [3,
с.116-119]. Наряду с этим, предельный переход
можно рассматривать как реализацию замысла о превращении 
в пространство
(см. п.3.5).
Важно
отметить, что об устойчивости вычислительной процедуры п.4.6, с использованием
предельного перехода 
можно судить по линейной зависимости между коэффициентами Фурье 
и 
– соответственно искомой функции
функции
удовлетворяющей уравнению (4.40),
и свободного члена
из (4.1), см. (4.76),
(4.77) и (4.78).
Характерным
представляется следующий момент. При подстановке выражений (4.71)
и (4.72) с 
то есть (4.79), – (4.40)
не изменяет в качестве интегрального уравнения Фредгольма второго рода своего
статуса. В этой связи следует отметить, что разложение
в ряд (4.66) – лишь один
из возможных способов его решения. Если осуществить такую же подстановку в (4.41),
численно найти
из уравнения (4.40) и
затем функцию
то
будет определяться путем ее умножения на коэффициент
см. (4.77). Вместе с тем,
узнать об этом оказалось возможным лишь на основании преобразований с параметром
и устремления его к 
Доказательство
удовлетворения
уравнению (4.1), см. п.4.5,
– очень важный момент, смысл которого заключается в следующем. При выводе уравнения
(4.52) использовалось
условие, касающееся тождественности решений уравнений (4.25)
и (4.35), однако в неявном
виде. Анализ фактически произведенных выкладок позволил сделать вывод о том,
что это условие действительно выполняется и функция
определяемая посредством решения (4.52),
удовлетворяет уравнению (4.1).
Тем
самым, по существу, подтверждена возможность реализации в (4.52)
свободного члена
адекватного подстановке на место
функции, результатом интегрирования которой по формуле (4.1)
является 
Известен целый ряд работ, в которых рассматриваются вопросы возмущения линейных операторов ([4, 5, п.7] и другие). В них исследованы, главным образом, вполне непрерывные возмущения, а также возмущения спектра. Нулевая погрешность (4.4) представляет собой не вполне непрерывное возмущение. Как показано в п.4.4, такое возмущение (в отличие от вполне непрерывного) может качественно изменить постановку задачи и привнести принципиально новые возможности ее численной реализации.
Необходимым в этой связи является условие (4.6),
обращающееся затем в (4.81).
Действительно, возникает (4.8)
– интегральное уравнение Фредгольма второго рода относительно искомой функции
создающее предпосылки далеко идущих преобразований. В совокупности, (4.4)
и (4.6) можно охарактеризовать
как определяющий фактор построения устойчивого алгоритма численной реализации
задачи (4.1).
И все же, этого для проведения преобразований п.4 – недостаточно. Пусть
в (4.4) 
и вместо (4.5) оператор
 |
(5.9) |
Для однозначной разрешимости уравнения (4.7)
здесь также требуется ядро 
обладающее свойством замкнутости. Поэтому его можно принять в виде (4.13).
Вместо (4.8) теперь
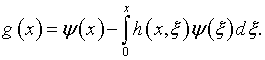
Распространяя с учетом данного обстоятельства уравнение (4.7)
на
как в п.4.3, получаем:
 |
(5.10) |
 |
(5.11) |
где – неопределенная
функция.
Решение уравнения (5.11)
выражается через резольвенту ядра
Его подстановка в (5.10)
приводит к уравнению вида
где –
функция, зависящая от 
Однако, его сопряжение с уравнением (5.11)
невозможно; то есть, процедура распространения на
– реально ничего не дает. Причина – отсутствие в уравнении (5.11)
функции 
Если же распространение (5.10)
на 
выполнить с участием определенного интеграла от 
то получится алгоритм п.4.4 в усложненном варианте.
Вместе с тем, настоящая причина непригодности оператора (5.9) для использования в (4.5) кроется глубже. Суть в качественного характера несоответствии между областями значений интегральных операторов Фредгольма и Вольтерра первого рода. Если в первом случае решение соответствующего уравнения существует лишь при выполнении условий теоремы Пикара, то во втором – для его определения достаточно, чтобы ядро и свободный член были непрерывными.*
В свете сказанного, следует отметить второй фактор достигаемой результативности.
Он связан с собственно распространением уравнения (4.4),
в котором оператор 
имеет вид (4.5), при условии
(4.6), на
согласно (4.23). При этом
решение уравнения (4.24)
на 
содержит функцию
соответственно в явном виде и только под интегралом. Данное обстоятельство представляет
собой существенную предпосылку получения относительно
интегрального уравнения Фредгольма второго рода.
Третий фактор состоит в использовании наряду с (4.24),
(4.34) уравнений (4.25)
и (4.35). С их помощью
построение алгоритма переходит в плоскость практической реализации. В процессе
приведения (4.35) к уравнению
(4.34), имеющему такое
же решение на 
получены основные расчетные соотношения.
И, наконец, четвертый фактор связан с, собственно, выбором ядра который
позволил:
- осуществить преобразования в аналитическом виде, вплоть до их заключительной части;
- определить функцию
при данных (4.1) из пространства
путем предельного перехода в решении, полученном для случая, когда
В дополнение к этому, ядро (4.13)
имеет еще целый спектр позитивных свойств: замкнутость; симметричность; непрерывность
и положительная определенность; зависимость от разности аргументов, а также
ортогональность собственных функций оператора
на интервалах как 
так и 
Перейдем к вопросу, который связан с уравнением (4.40).
При 
в (4.71) и (4.72)
имеем (4.79), соответственно
уравнение (4.40) приобретает
вид:
 |
(5.12) |
или же
 |
(5.13) |
что делает его весьма любопытным. Получается, вместо некорректной задачи в качестве базового объекта исследования фактически выступает интегральное уравнение Фредгольма второго рода, полученное, всего лишь, прибавлением к (4.1) искомой функции с коэффициентом, совокупность допустимых значений которого практически не ограничена.
В самом деле, при 
: 
параметр 
нетрудно выбрать так, чтобы решение однородного уравнения (5.12),
то есть
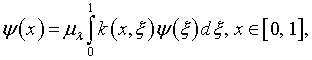
где
 |
(5.14) |
было тривиальным.
Заметим, что при вычислении функции 
информация о данных задачи, содержащаяся в
претерпевает существенное видоизменение, в котором участвуют ядро и свободный
член уравнения (4.1). Одновременно
следующий этап выкладок, который состоит в определении
переносится с
на 
После этого, то есть при вычислении коэффициентов Фурье функций
и
новой информации о данных задачи не вносится. По существу, коэффициенты Фурье
функции
троекратно умножаются на соответствующие константы. Вместе с тем, обратившись
к системе уравнений (4.78),
можно заметить, что зависимость между коэффициентами Фурье функций
и
то есть соответственно 
и 
имеет весьма содержательный смысл, вследствие (4.70)
и (4.74).
Если функцию 
из (4.39) подставить в
(5.12), то с учетом (4.1)
и (5.14) получаем
 |
(5.15) |
где
из чего можно сделать довольно интересные, как представляется, выводы:
1) Существует интегральное уравнение Фредгольма
второго рода с ядром 
из (4.1) и параметром (5.14),
свободный член которого, за вычетом 
такой же как у полностью идентичного уравнения относительно искомой функции
При этом
где
– решение также интегрального уравнения Фредгольма второго рода (5.12).
2) И, наоборот, функция
удовлетворяющая (4.1),
выражается из (5.15) через
решение интегрального уравнения Фредгольма второго рода (4.36)
и данные задачи. Заметим, что в результате вычитания уравнений (4.36)
и (5.15) функцию 
можно представить интегрально зависящей от 
3) При 
уравнение (5.13) обращается
в (4.1). Вместе с тем,
при другом значении параметра
решение этого уравнения – корректная задача и, как показано выше, через него
с помощью устойчивой процедуры численной реализации определяется
Таким образом, уравнению (4.1)
соответствует множеству корректно поставленных задач, при критических значениях
содержащегося в них параметра.
Итак, функции 
и
в (4.39) взаимосвязаны
между собой посредством интегрального оператора Фредгольма (4.5).
Как представляется, обозначен существенный момент, вполне заслуживающий дальнейшей
интерпретации.
Следующий вопрос связан с возможностью реализации других способов
определения функции 
или же 
с помощью которых по формулам (4.28),
(4.30) находится решение
задачи. Один из них наметим схематично: подстановка в (5.2)
из (4.30) и (4.40)
 |
(5.16) |
подстановка 
в (4.28); исключение
из выражений (4.28) и
(4.30).
Однако при этом ядро интегрального уравнения, из которого определяется
будет аналитически зависящим от параметра 
вследствие чего возникают ненужные осложнения. Суть в том, что, вообще говоря,
подобные уравнения могут быть неразрешимыми вне зависимости от значения параметра
[6, с.130-132; 7].
В целом, подход к решению задачи, связанный с использованием (5.16),
представляется менее эффективным.
Аналог уравнения (4.52)
можно построить и относительно функции 
Для этого в (5.2) следует
подставить 
из (4.39), где функция
имеет вид (4.28), то есть
В результате
 |
(5.17) |
где 
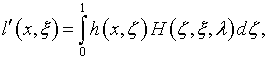
сопоставление с (4.53),
учитывая (4.19), (4.21),
показывает, что 
 |
(5.18) |
По
сравнению с алгоритмом п.4.4, в этом случае отпадает необходимость промежуточного
определения функции 
не
дающая, впрочем, существенного упрощения вычислений.
Заметим,
что если свободный член
имеет разрывы или другие особенности, обусловленные ядром 
то может оказаться желательным, чтобы он присутствовал в решении явно. Для этого
функцию
следует выразить через
с помощью уравнения (4.34).
Что касается удовлетворения уравнению (4.24),
то оно осуществляется вследствие использования (4.31)
при построении уравнения (4.52).*
Возвращаясь в заключение настоящего подраздела к условию (4.3),
обратим внимание на адаптивность привязки
к пространству 
а также логику ее практической реализации. Предварительно, – основные факты
об отображении (4.1) между
и 
вне зависимости от предлагаемого использования 
Итак, область значений 
не
является замкнутой, вследствие чего оператор – не
вполне непрерывный и обратный ему 
из
в
– ограничен. Однако, в рамках традиционного объекта исследования – (4.1)
отсутствует возможность каким-то образом использовать данное обстоятельство
для построения оператора 
И вместе с тем, возникает следующая цепочка соображений:
- объективно, ограниченный оператор
из
существует, то есть решение уравнения (4.1)
в паре пространств 
– корректная задача;
- свойство
ограниченной обратимости непосредственно ассоциируется с интегральным оператором
Фредгольма второго рода, в нашем случае 
- внедрение в схему преобразований тождественного
оператора 
органично сочетается с моделированием погрешности интегрирования, порождающей
(в совокупности с первопричиной – незамкнутость
) некорректность задачи (4.1);
- адаптация к
пространству и
функциональное представление погрешности, таким образом, тесно взаимосвязаны;
- незамкнутость
никак не препятствует определению функции
из уравнения (5.12), через
которую, как показано выше, находится решение задачи – функция 
- с этой точки зрения, уравнение, (4.7),
следующее из (4.4), (4.6),
осуществляет сопряжение интегральных операторов Фредгольма первого и второго
рода через их общую область значений, создавая серьезную предпосылку к решению
задачи об определении функции
удовлетворяющей (4.1),
в корректной постановке.
Обозначенная направленность будет развита в следующем подразделе.
Здесь выкладки пп. 4.2 – 4.4 распространяются на случай, когда данные уравнения
(4.1), то есть
и 
а также удовлетворяющая ему функция
– изначально принадлежат пространству
Ядро
имеет прежний вид (4.13);
параметр 
– фиксирован.*
Обратимся к уравнению (4.24):
 |
(5.19) |
или
 |
(5.20) |
 |
(5.21) |
проистекающему из представления погрешности (4.4),
при условии (4.6), и распространения
(5.20) на 
Возможность
удовлетворения этому уравнению на интервале 
с помощью 
рассматривалась в п.4.2 (функция
выступала в качестве данной). Для того чтобы выполнить условие (4.6),
подразумевающее приближение в пространстве 
класс возможной принадлежности
пришлось ограничить гармоническими функциями.
При этом, по существу, вопрос сводится к исследованию разрешимости интегрального уравнения Фредгольма первого рода (4.10), определяемой условиями теоремы Пикара [2]:
 |
(5.22) |
где 
– характеристические числа и собственные функции ядра (4.11),
перенумерованные в порядке их следования, см. (4.12).
Кроме того, система собственных функций 
должна быть полной на интервале 
и ядро 
– вещественным симметричным, что в данном случае заведомо имеет место.
И,
тем не менее, как показал Э.Гурса [8,
с.143-144], если даже условие (5.22)
не выполняется, всегда можно найти такую функцию 
что интеграл
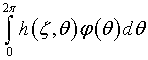
будет отличаться от 
из (4.10), в среднем –
сколь угодно мало. Следует отметить, что
при этом предполагается ядром гораздо более общего вида, нежели (4.11).
Доказательство основывается на совпадении
где
 |
(5.23) |
с суммой первых членов ряда Фурье функции 
по
элементам 
Поэтому
можно установить значение 
при
котором интеграл
окажется меньше некоторого 
Однако,
удовлетворяя таким образом уравнению (4.10),
с ростом 
ряд (5.23) будет расходиться
в пространстве
Соответственно не представляется возможным рассматривать (5.19)
как интегральное уравнение Фредгольма второго рода относительно функции
 |
(5.24) |
и производить обращение
оператора 
Согласно позднее утвердившейся терминологии,
трактуется в качестве обобщенной функции – распределения [9,
п.2.1.5; 10, п.12].
Итак,
существует функция 
удовлетворяющая уравнению (5.20),
или же (4.7) в смысле
где оператор
имеет вид (4.5); 
и произведена замена переменных (4.9).
Вместе
с тем, фактически используемое ядро (4.13)
– бесконечнодифференцируемо и периодически зависит от 
что позволяет понимать
как обобщенную функцию в менее ограничительном смысле сходимости ряда (5.23)
[11, с.17-18]:
 |
(5.25) |
(переменная 
играет
роль параметра).
Действительно, подстановка в (5.25) выражений (5.23) и (4.19), с использованием также (4.17) и переобозначения коэффициентов, сводится к следующему:
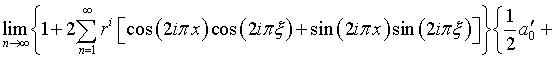
Далее
функция
будет определяться из уравнения, построенного на базе соотношения (5.2).* С использованием (4.39)
оно принимает вид:
 |
(5.26) |
где
– решение интегрального уравнения Фредгольма второго рода (4.40).
При
этом в (5.26) совсем не
обязательно подставлять функцию
из (4.28).* Достаточно выразить через
интеграл
что равносильно приданию также и смысла
обобщенной функции.
Реализуя
уже в объективно этом качестве
проинтегрируем с ядром
уравнения (5.20) и (5.21)
в пределах соответственно 
и 
Получаем
 |
(5.27) |
 |
(5.28) |
где
 |
(5.29) |
Поскольку
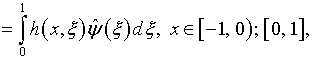
вследствие
см. (4.19), уравнения (5.27) и (5.28) эквивалентны следующим:
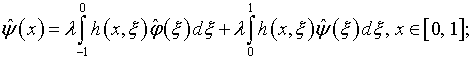
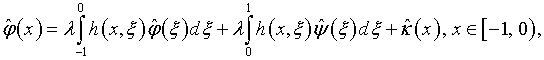
или
 |
(5.30) |
где
 |
(5.31) |
(обратим внимание, вновь позитивную роль сыграл выбор ядра ).
То
есть, получен точный аналог уравнения (5.19),
в котором функция (5.24)
заменена обобщенной – (5.31).
Обращение оператора 
в (5.30) дает
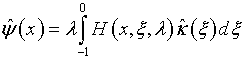
(аналог (4.28)), вследствие чего выражение (5.26), с учетом (5.29) и (5.18) приобретает вид:
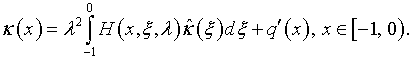
Подстановка
из (5.29), поскольку
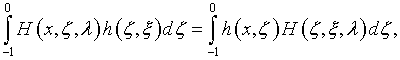
см. (4.53), (4.19) и (4.21), приводит к тому же самому уравнению (5.17). Таким образом, использование обобщенных функций обеспечило в данном случае законность выкладок, не оказав влияния на конечный результат их проведения.
Обратимся далее к уравнениям (4.34) и (4.35):
 |
(5.32) |
 |
(5.33) |
где
– оператор (4.5).
Как
показано выше, превращение (5.33)
в уравнение (5.32), или
же наоборот, с помощью соотношений (4.32),
(5.2), (5.3),
а также других, позволяет получить интегральные уравнения Фредгольма второго
рода (4.52), (5.17),
решения которых, при соответствующем установлении параметров 
существуют и единственны. Для конкретно выбранного ядра
будь-то выражение (4.13)
или другое, они зависят исключительно от данных задачи.
Существуют
и единственны в таком смысле и решения уравнений (5.32),
(5.33), когда их свободные
члены, включающие функции 
предполагаются данными. Действительно, обращение в (5.32)
оператора
приводит к интегральному уравнению Фредгольма второго рода:*
 |
(5.34) |
Здесь
 |
(5.35) |
 |
(5.36) |
где 
– резольвента (4.21).
Это уравнение отличается от (4.40)
всего лишь компонентой свободного члена, и его решение находится аналогично.
Зная
можно вычислить
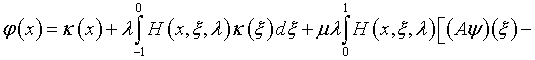
(то же самое нетрудно проделать и с уравнением (5.33)).
Входящая
в выражение (5.36) функция
находится из уравнения (5.17),
решение которого
 |
(5.37) |
где 
– резольвента (4.56);
функция 
определяется выражением (5.18).
Последнее
зависит от функции
которая, в свою очередь, представляет решение интегрального уравнения Фредгольма
второго рода (4.40). При
этом предполагается выполнение (4.59)
– условий в отношении параметра 
Значение
принимается так, чтобы уравнение (4.60)
не имело нетривиальных решений.
Общая
последовательность вычислительных процедур, после того как найдена функция состоит
в определении:
- функции
– по формуле (5.18);
- функции
– по формуле (5.37);*
- ядра и свободного члена уравнения (5.34) – по формулам (5.35), (5.36);
- искомой
функции
– из уравнения (5.34).
Доказательство удовлетворения получаемого таким образом решения уравнению (4.1) производится аналогично изложенному в п.4.5.
Кратко коснемся численной реализации уравнений (4.40) и (5.34). Как известно, для решения интегральных уравнений Фредгольма второго рода, включая вычисление спектральных характеристик и квадратур, имеется целый ряд устойчивых алгоритмов. Наряду с руководством, которое указано в п.4 под №5, они приведены в [12, 13] и целом ряде других изданий. При этом освещаются, вообще говоря, созвучные подходы.
Можно выделить алгоритм численной реализации резольвенты С.Г.Михлина [14, п.12], базирующийся на конечно-элементной аппроксимации ядра интегрального уравнения. Особенно интересным представляется метод Г.Н.Положего [15], преобразующий интегральное уравнение Фредгольма второго рода так, что его решение, вне зависимости от значения параметра, достигается с помощью простых итераций. В этой связи установлено начальное приближение и используется второе итерированное ядро.
Для сходимости в среднем простых итераций к решению уравнения (5.34) требуется, чтобы
 |
(5.38) |
где
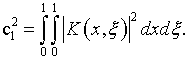
Если же
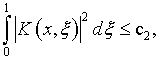
где 
– постоянная, и выполнено условие (5.38),
то соответствующий ряд Неймана сходится абсолютно и равномерно [16].
Заметим, что возможность варьирования параметром 
создает
дополнительный резерв повышения эффективности процедуры численной реализации.
Вместо (4.13) в выкладках
настоящего подраздела могло бы использоваться и другое ядро
Вместе с тем, многочисленные достоинства ядра Пуассона, о которых говорилось
выше, делают такую замену совершенно излишней. Действительно, если
удовлетворяет условиям теоремы Мерсера, отказываться от чего не имеет ни какого
смысла, то [2, с.166]:
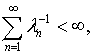
и в качестве характеристических чисел альтернативного ядра можно было бы принять, например, величины, обратные членам сходящейся арифметической или же геометрической прогрессии. Получить от этого какую-либо выгоду весьма проблематично, наряду с чем, некоторые из имеющихся преимуществ могут быть утеряны.
Обсудим вопрос об адаптации уравнения (4.1)
к пространству
(определяемому условием (5.22)),
который неоднократно затрагивался выше. Итак,
– область значений оператора
не является замкнутой, чем обуславливаются все сложности определения функции
удовлетворяющей уравнению (4.1),
в постановке решения интегрального уравнения Фредгольма первого рода.
Что касается (5.32),
то здесь отмеченное обстоятельство не имеет значения, поскольку, обращая оператор
получаем интегральное уравнение Фредгольма второго рода, а именно (5.34).
Вместе с тем, построение уравнения (5.32)
осуществляет весьма интересный субъект, а именно (4.7).
Это интегральное уравнение Фредгольма как первого, так и второго рода, относительно
функций соответственно 
и
Однако в первом из указанных качеств оно принципиально отличается от (4.1)
тем, что свободный член 
определяемый выражением (4.8),
не принимая конкретных значений, зависит от искомой функции
Поэтому, можно полагать, что
где оператор
и, как представляется, элемент упомянутой выше адаптивности – налицо.
Затем, в результате распространения (4.7)
на
появилось интегральное уравнение Фредгольма второго рода (4.24)
относительно 
см. (5.24), с функцией
представляющей его свободный член. В самом деле, зная
путем обращения оператора
можно определить функцию
а также и 
Заметим, однако, – от нахождения функции
содержащейся под интегралом (4.1),
задача превратилась в определение функции 
которая входит явно!
Как вновь не обратиться к доводам Ж.Адамара
о существовании корректных постановок физически содержательных задач, а также
неоднократно звучавшему в тексте предложению рассматривать (4.1)
как правило, по которому осуществляется интегрирование функции
? Суть в том, что будучи подставлена в некоторое интегральное уравнение Фредгольма
второго рода, эта функция порождает соответствующий свободный член. Следовательно,
задача сводится к процедуре его определения, которая имеет мощный ресурс, а
именно возможность произвольно выбирать (на самом деле, каким-то образом выстраивать)
ядро интегрального уравнения.
Можно предположить, что здесь реализован лишь один из ряда существующих
подходов обозначенной направленности. Если имеется столь благоприятный объект
как интегральное уравнение Фредгольма второго рода и свободный член, при котором
ему удовлетворяет функция объективно
существует, – то нет альтернативы корректной постановке задач математической физики!
Возвращаясь к алгоритму, проследим как конкретно такая постановка осуществлялась.
Итак, найдена функция 
– часть решения (5.34),
обусловленная 
Свойства используемого при этом уравнения (4.40),
в вычислительном отношении, – превосходные.
Исключение из (5.33)
компоненты решения, зависящей от
привело к соотношению (5.2);
с его помощью посредством резольвенты определена функция 
Она и есть – свободный член, к определению которого сведена задача. В этой связи,
учитывая также (5.37),
еще раз обратим внимание на (4.28),
(4.30) – представления
– соответственно «интегральное» и с функцией
входящей явно. Их варьирование при проведении преобразований в интересах реализации
устойчивой процедуры вычисления функции 
явилось одним из определяющих факторов.
Таким образом, задача (4.1) превратилась в решение интегрального уравнения Фредгольма второго рода (5.34), вычитая из которого (4.40), с учетом (4.39), получаем
 |
(5.39) |
где
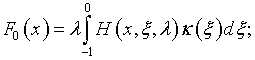
функция
определяется выражениями (5.37)
и (5.18). Действительно,
– та же функция, которая содержится в (4.36).
Это следует из уравнений (4.34),
(4.35), а также представлений
решения (4.28) и (4.31),
то есть
Итак,
функцию
можно определить, сложив решения уравнений (4.40)
и (5.39):
После
нахождения функции 
задачу можно решать также, используя подстановку выражения (5.26)
в (4.28). При этом функция
удовлетворяет интегральному уравнению Фредгольма второго рода
 |
(5.40) |
где
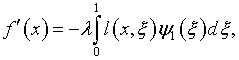
см. также (4.55).
Соответственно решение (5.40) выражается через резольвенту (4.56):
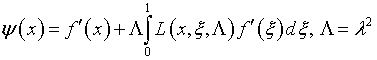
и, как можно заметить, в этом случае численно решается лишь одно интегральное уравнение Фредгольма второго рода – (4.40). Затем производятся исключительно процедуры интегрирования.
Уравнения (4.40) и (5.39), или же (4.40), с использованием, (5.40), данные которых оговорены выше, олицетворяют собой задачу (4.1) в ее корректной постановке!
Если сопоставлять алгоритмы пп. 4.4, 4.6 и настоящего подраздела, то, конечно, второй из них более формализован, что может оказаться в некотором смысле предпочтительным.
Поскольку необходимые формулы разбросаны по тексту, представляется целесообразным привести их последовательно и в наиболее удобной для проведения вычислений форме.
В
предположении о том, что 
и
ядро 
–
замкнуто, функция, удовлетворяющая уравнению
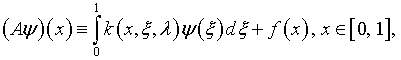
определяется как
 |
(5.41) |
где и
–
решения интегрального уравнения Фредгольма второго рода
 |
(5.42) |
при свободном члене соответственно:
 |
(5.43) |
 |
(5.44) |
(в привязке к уравнению (4.40),
).
Ядро уравнения (5.42)
 |
(5.45) |
Здесь и выше
 |
(5.46) |
где параметр 
 |
(5.47) |
(в привязке к (5.18),
).
В
этом выражении
 |
(5.48) |
где
 |
(5.49) |
 |
(5.50) |
Параметр
параметр
где 
–
характеристические числа однородного уравнения
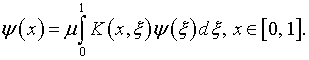
После
выбора значений 
и
(которые
затем могут, исходя из различных соображений, корректироваться) последовательность
вычислительных процедур заключается в определении:
- ядра
уравнения (5.42) – по
формуле (5.45), с использованием
выражения (5.46);
- свободного
члена 
– по формуле (5.44);
- функции
– из уравнения (5.42),
с 
- функции
– по формуле (5.48), с
использованием выражения (5.49);
- функции
– по формуле (5.47) с
использованием выражения (5.50);
- свободного
члена 
– по формуле (5.43);
- функции
– из уравнения (5.42),
с 
- искомой
функции
– по формуле (5.41).
