| |
|
|
|
4.2. Модель представления погрешности
4.3. Трансформированная постановка задачи
4.4. Конструктивный алгоритм практической реализации
4.5. Достоверность полученного решения
4.6. Решение – произвольная функция из 
В свете соображений пп. 1.4 и 3.5, продолжим рассмотрение интегрального уравнения Фредгольма первого рода
 |
(4.1) |
предполагая, что
его решение существует и единственно; ядро 
и свободный член 
принадлежат пространству 
Или, по терминологии [1],
они являются
-функциями:
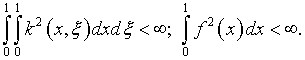
Однако, на самом
деле, определение функции 
по данным 
и 
будет производиться не в постановке решения интегрального уравнения Фредгольма
первого рода (4.1), а исходя
из следующих соображений. Имеется оператор 
описывающий некоторое явление. Это описание выражается в интегрировании функции
по формуле (4.1).
Вычисление
осуществляется
с погрешностью, которую обозначим через 
где
– постоянная.
В большинстве случаев эта погрешность, вследствие своей малости, несущественна,
или же может быть снижена до требуемого уровня. Тем не менее, вычислительная процедура
допускает интерпретацию:
 |
(4.2) |
Ситуация кардинально
изменится, если, наоборот, поставить задачу о восстановлении функции
по информации, содержащейся в (4.1),
то есть
и 
Действительно, такая задача является в общем случае некорректной, что по существу
означает неразрешимость уравнения (4.1).
С этой точки
зрения, уравнение (4.2)
отличается наличием потенциала приведения задачи к поставленной корректно. Необходимое
для этого условие состоит в представлении погрешности 
так, чтобы вне зависимости от данных (4.1)
и функции
–
 |
(4.3) |
где 
– область значений оператора 
Иначе говоря, оператор 
см. (3.6), должен сообщить
алгоритму адаптационные начала.
Итак, ставится
следующая задача: по данным
и
конструктивно определить функцию 
которая, будучи подставлена в (4.1),
удовлетворила бы этому уравнению. Здесь конструктивизм подразумевает возможность
использования устойчивой процедуры численной реализации, вследствие сведения
задачи к решению интегрального уравнения Фредгольма второго рода.*
Базой последующих
выкладок будет служить уравнение (4.2),
в котором определяющим является установление адекватной взаимозависимости между
и 
Уравнение (4.1) рассматривается
исключительно в контексте прямой задачи вычисления интеграла, и как источник
исходной информации.
Следуя сказанному
в п.3.5, выразим погрешность вычисления
по формуле (4.1) разностью
искомой функции
и интегральной компоненты:
 |
(4.4) |
где 
– постоянная;
оператор
 |
(4.5) |
о ядре 
будет
сказано ниже.
Однако предполагается
построение устойчивого алгоритма вычисления функции
удовлетворяющей уравнению (4.1),
и, следовательно, малые вариации данных не должны существенно влиять на решение.
В этой связи рассмотрим возможность выполнить условие
 |
(4.6) |
допуская, тем самым, что конструктивно разрешить задачу, сформулированную в п.4.1, удастся с помощью (всего лишь) прибавления к свободному члену уравнения (4.1) «нуля» из (4.4), имеющего следующий вид:*
Это уравнение можно представить так:
 |
(4.7) |
где
 |
(4.8) |
и с помощью замены переменных
 |
(4.9) |
привести к каноническому виду
 |
(4.10) |
Очевидно, выполнение
условия (4.6) эквивалентно
разрешимости этого уравнения. Пусть ядро 
принадлежит пространству
и замкнуто. В таком случае (4.10)
является интегральным уравнением Фредгольма первого рода, решение которого,
если оно существует, единственно [1].
Удовлетворяя указанные требования, представим (4.10)
в виде интеграла Пуассона [2,
с. 202-205]. Соответственно ядро
 |
(4.11) |
его характеристические
числа и ортонормированные на 
собственные функции [1,
с.187-188]:
 |
(4.12) |
при этом в (4.7)
 |
(4.13) |
Если в уравнении (4.10) функция
 |
(4.14) |
где 
и 
– коэффициенты
ее разложения в ряд Фурье, абсолютно интегрируема, то есть
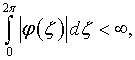
функция
 |
(4.15) |
представляет собой действительную часть аналитической внутри единичного круга функции и является гармонической [3, с.160-161; 4]:
где 
– декартовы координаты.*
Поскольку указанное
свойство не зависит от линейной замены переменных, из (4.8)
с учетом (4.9) и (4.15)
следует, что при условии (4.6)
функция
удовлетворяющая уравнению (4.1),
может быть только гармонической. То есть, – принадлежащей классу функций, значительно
более узкому, нежели предполагалось постановкой задачи в п.4.1.
И все же, можно
сделать вывод о том, что «нулевая» погрешность интегрирования гармонической
функции
по формуле (4.1) действительно
представима в виде (4.4)
при ядре
из (4.13). Это важный
момент изложения.
Компоненты (4.12) удовлетворяют однородному уравнению
которое путем замены переменных
преобразуется следующим образом:
 |
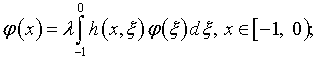
(4.16) |
позволяя, с учетом
также (4.12), (4.9),
определить характеристические числа и ортонормированные на 
собственные функции ядра (4.13):
|
(4.17) |
Решение задачи
(4.1) является единственным.
Соответственно из сопоставления однородного интегрального уравнения Фредгольма
второго рода относительно
отвечающего (4.8) (то есть
при 
), и (4.16) вытекает условие:
 |
(4.18) |
Так как ядро
в (4.16) симметрично,
непрерывно и все 
то на основании теоремы Мерсера [1]
 |
(4.19) |
причем этот ряд сходится абсолютно и равномерно.
Далее потребуется
резольвента оператора 
Из билинейного разложения (4.19),
при использовании той же теоремы Мерсера, следует, что характеристические числа
и ортонормированные на 
собственные функции его ядра имеют вид
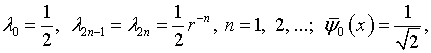
а значит необходимо поставить еще одно условие:
 |
(4.20) |
Следует принять
во внимание, что использование теоремы Мерсера явилось отличным от предшествовавшего
представления ядра
рядом (4.19). Здесь, напротив,
существует разложение ядра
в равномерно сходящийся билинейный ряд по ортогональной на 
системе элементов. Соответственно, эти элементы, с поправкой на нормирующий
множитель, и значения 
представляют собой собственные функции и характеристические числа оператора
Заметим
также, что функции 
ортогональны
не только на 
но
и на 
Данное
обстоятельство сыграет ниже весьма важную роль в плане упрощения процедуры численной
реализации.
Резольвента ядра (4.5) определяется рядом [1]:
 |
(4.21) |
который при условии (4.20) также сходится абсолютно и равномерно.
Из (4.8) и (4.15), с учетом (4.9),
таким образом, при условии (4.6) уравнение (4.1) может быть удовлетворено лишь в случае, когда
 |
(4.22) |
При проведении
последующих выкладок предполагается, что функция 
– гармоническая и свободный член уравнения (4.1)
имеет вид (4.22). Данное
обстоятельство, о чем уже упоминалось, резко сужает круг практических приложений.
Как будет показано (п.4.6), полученное для такого случая решение путем предельного
перехода 
превращается в
-функцию
которая удовлетворяет уравнению (4.1).*
Распространим уравнение (4.4) при условии (4.6) следующим образом:
 |
(4.23) |
где 
вследствие (4.14), – некоторая
неопределенная функция.
Уравнение, объединяющее (4.7) и (4.23), представим в виде
 |
(4.24) |
то есть
Введем также взаимосвязанное с ним и близкое по своей структуре уравнение:
 |
(4.25) |
где 
и 
– еще
две неопределенные функции (как и 
они
– гармонические). Целесообразность такого шага будет раскрыта в процессе дальнейшего
изложения.
Представить
процедуру построения уравнений (4.24)
и (4.25), с практической
точки зрения, несложно. Есть гармоническая функция
которая интегрируется согласно (4.1).
Как показано выше, существуют ядро
и абсолютно интегрируемая функция 
при которых уравнение (4.24)
удовлетворяется на 
Можно предположить, что каким-то образом функция 
определена. Теперь как
так и
– данные функции. Уравнение (4.24)
на 
а также и в целом удовлетворяется посредством функции 
Вновь дана 
Функция
определяется из уравнения (4.25)
на 
:
 |
(4.26) |
Относительно
– это интегральное уравнение Фредгольма второго рода. На основании положений
общей теории [1], при
условии (4.18) решение
уравнения (4.26) существует
и единственно. Есть данные функции
– уравнение (4.25) на
и в целом удовлетворяется посредством 
Если использовать обозначения
 |
(4.27) |
то (4.24),
(4.25) представляют собой
интегральные уравнения Фредгольма второго рода относительно 
и 
со свободными членами соответственно
При условии (4.20) решения этих уравнений:
 |
(4.28) |
 |
(4.29) |
и
 |
(4.30) |
 |
(4.31) |
где 
– резольвента оператора 
имеющая вид (4.21).
Вычитая (4.25) из уравнения (4.24), получаем
 |
(4.32) |
 |
(4.33) |
Из этих соотношений
следует, что функцию 
через 
можно выразить конструктивно, то есть с помощью решения интегрального уравнения
Фредгольма второго рода. Действительно, при условии (4.18)
определяется через резольвенту ядра
в (4.33). Однако обратная
процедура, то есть представление функции
через 
была бы сопряжена с решением интегрального уравнения Фредгольма первого рода.
К уравнениям
(4.24), (4.25)
прибавим «нуль» из (4.1),
а именно 
со свободным членом вида (4.22),
получая соответственно
 |
(4.34) |
 |
(4.35) |
Итак, вместо некорректной задачи (4.1), далее будут рассматриваться две системы интегральных уравнений (4.24), (4.34) и (4.25), (4.35).*
Дальнейшая направленность
выкладок в некотором смысле противоположна предыдущей. Действительно, выше фактически
предпринималось все возможное (начиная с модели погрешности (4.4))
для того, чтобы искомая функция
а также
и
находились, в специально для этого построенных уравнениях, не только под интегралом,
но и в явном виде. Вследствие этого получено (4.30)
– представление решения
с функцией
также в явном виде.
Было бы весьма
желательным вывести другое представление
содержащее, очевидно, и данные задачи (4.1),
в котором, напротив, функция
находилась только под интегралом. Исключение
в нем и (4.30) позволило
бы получить интегральное уравнение Фредгольма второго рода относительно
Еще один вариант
достижения той же цели состоит в определении подынтегрального выражения (4.32)
через
Поскольку функция
в этом смысле известна (см. (4.31)),
возникает необходимость установления зависимости между 
и данными задачи.
Осуществление
как одного, так и другого из обозначенных вариантов можно представить в контексте
приведения (4.35) к виду
(4.34). Основанием служит
вхождение в каждое из этих уравнений функции
а также аналогичность их структуры. Это наводящие соображения.
Для исключения
функции
из (4.35) используем уравнение
 |
(4.36) |
в результате вычитания которого
 |
(4.37) |
или
 |
(4.38) |
где
 |
(4.39) |
Если обозначить
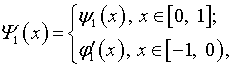
то (4.38) приобретает вид
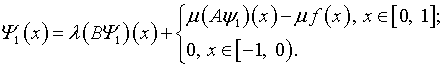
Относительно
– это интегральное уравнение Фредгольма второго рода. Обращая оператор 
при условии (4.20), с
учетом (4.1) получаем
 |
(4.40) |
 |
(4.41) |
где
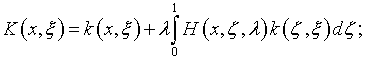
Таким образом, функция 
определяется из интегрального уравнения Фредгольма второго рода (4.40)
и зависит только от данных (4.1),
а также выбранного ядра 
* При этом предполагается, что
где 
– характеристические числа однородного уравнения, которое получается из (4.40)
в случае 
Значения 
как и решение уравнения (4.40),
находятся с помощью приближенных методов [5].
После этого, функция 
вычисляется по формуле (4.41).
Однако (4.37) может
рассматриваться и как уравнение (4.34).
Действительно, произведенное исключение
из уравнения (4.35) равносильно,
образно выражаясь, перетеканию этой функции в 
с появлением уравнения (4.34).
Требуется, следовательно, идентифицировать функции
и
из (4.34) в структуре
уравнения (4.37).
Воспользуемся для этого уравнением (4.37)
на
:
 |
(4.42) |
обратив внимание на способ его получения. Он состоит в
исключении из уравнения (4.35)
части решения, зависящей от компоненты свободного члена
Однако при этом изменились функции, удовлетворяющие данному уравнению, как на
так и на
Иначе говоря, видоизменились обе функции 
и 
Вместе с тем, структура уравнений (4.34),
(4.35) предполагает превращение
одного из них в другое путем изменения содержащихся функций только на
то есть
и 
* Поэтому
в уравнении (4.42) скорректируем
так, чтобы исключилось слагаемое с функцией 
Соответственно к
следует отнести члены уравнения (4.42),
содержащие функцию 
В результате появляются соотношения:
 |
(4.43) |
 |
(4.44) |
Здесь 
–
решение интегрального уравнения Фредгольма второго рода
 |
(4.45) |
где
при условии (4.18).
Вычитая (4.45) из уравнения (4.42), получаем
 |
(4.46) |
Уравнение (4.35)
на
имеет вид
 |
(4.47) |
в результате его сопоставления с (4.46)
 |
(4.48) |
то есть от (4.42)
мы, по существу, возвратились к уравнению (4.35)
на 
причем таким способом, который позволил установить это соотношение.
Как можно заметить, соотношения (4.43),
(4.44) превращают (4.46)
в (4.23). Покажем, что
соотношения (4.43), (4.44)
и (4.48) действительно
преобразуют уравнение (4.35)
к виду (4.34). Обратимся для этого к уравнению
(4.35) на
:
 |
(4.49) |
Используя (4.44) и (4.32), получаем
где
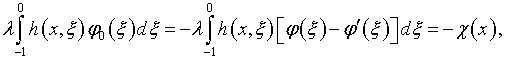
и путем подстановки приведенных выражений
(4.49) превращается в
уравнение (4.34) на
Подстановка функции
из (4.44) в (4.47),
с использованием (4.48)
и (4.43), приводит к уравнению
(4.34) на 
* Таким образом, с помощью установленных соотношений уравнение
(4.35) как на
так и на
превращается в уравнение (4.34).
 |
(4.50) |
вследствие чего выражение (4.32) приобретает вид
 |
(4.51) |
Вывод соотношений (4.43), (4.44), а также (4.48) и, наконец, (4.50) – представляет собой главное звено в построении алгоритма.
Подстановка в (4.51) выражения (4.31) приводит к интегральному уравнению Фредгольма второго рода:
 |
(4.52) |
где 
 |
(4.53) |
 |
(4.54) |
Выражение (4.53), после подстановки в него (4.19) и (4.21), принимает вид
 |
(4.55) |
где 
и 
– собственные функции (4.17),
являющиеся на 
ортонормированными. Данное обстоятельство позволяет определить резольвенту ядра
Действительно, его характеристические числа
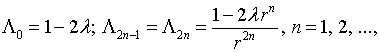
и, поскольку 
при ограниченном 
что предполагается, лишь конечное их количество может принимать отрицательные
значения. На основании теоремы Мерсера [1],
(4.55) представляет собой
билинейное разложение симметричного непрерывного ядра 
При условии
которое эквивалентно (4.20), его резольвента
 |
(4.56) |
вследствие чего решение уравнения (4.52) можно представить следующим образом:
 |
(4.57) |
Очевидно, для сходимости ряда (4.56), в дополнение (4.18) и (4.20), должно выполняться условие:
 |
(4.58) |
Подстановка выражения (4.57)
в (4.30), с использованием
(4.21), позволяет вычислить
функцию
являющуюся решением рассматриваемой задачи.
Процедура численной реализации включает этапы:
- конкретизация параметра 
- установление параметра
из условий (4.18), (4.20)
и (4.58), учитывая также
(4.4), то есть
 |
(4.59) |
- установление параметра
в (4.40) так, чтобы уравнение
 |
(4.60) |
имело лишь тривиальное решение;
- определение функции 
– из уравнения (4.40);
- вычисление функции 
– по формуле (4.41);
- вычисление функции 
– по формуле (4.54);
- вычисление функции
– по формуле (4.57);
- вычисление искомой функции
– по формуле (4.30).
Заметим, что реализация алгоритма связана с использованием квадратур и кубатурных формул в двумерной области [6]. Одновременно могут быть задействованы приемы улучшения сходимости тригонометрических рядов [7, с.187-193] и способы интегрирования осциллирующих функций [8, с.113-115].
Итак, функция
или же решение задачи (4.1)
в ее суженной постановке (см. п.4.2), находится по формуле (4.30).
Вместе с тем, выражения (4.28)
– (4.31), представляющие
собой решения уравнений (4.24),
(4.25), удовлетворяют
им тождественно, вне зависимости от того каковы функции
и
Поэтому нельзя на основании простого вычитания из (4.35)
уравнения (4.25) утверждать,
что решение последнего удовлетворяет также и уравнению (4.1).
Такая возможность очевидна, но лишь при использовании в (4.25)
и (4.35) адекватной функции
В общем случае, решения этих уравнений могут быть совершенно разными.
Требуется, следовательно, показать, что определяемая выражением
(4.30) функция
которая удовлетворяет совместно с
уравнению (4.25), является
также и решением уравнения (4.35)
на 
Для этого входящие в уравнения (4.24),
(4.25) и (4.34),
(4.35) функции 
целесообразно переобозначить соответственно как: 
и 
С помощью указанных пар уравнений получены соотношения соответственно, п.4.4:
 |
(4.61) |
и
см. (4.32) и (4.39), (4.44), (4.48), или
см. (4.50), наконец, в сокращенном виде
 |
(4.62) |
Однако фактически использовалось соотношение
 |
(4.63) |
где
см. (4.31), приведшее после подстановки в (4.61) к выражению
см. (4.51), из которого вытекает уравнение (4.52).
Иначе
говоря, в правую часть (4.62)
на место 
была подставлена функция 
В целом, получение (4.63)
явилось таким:
то есть были использованы две предпосылки
и соотношение (4.62).
Действительно, при выполнении этих тождеств соотношение (4.63) превращается в (4.62). Итак, можно сделать вывод о том, что указанные предпосылки, или же тождества
 |
(4.64) |
представляют собой условия, достаточные для сведения задачи (4.24), (4.34) и (4.25), (4.35) к решению уравнения (4.52).
Наряду с этим, они являются также и необходимыми. В самом деле, из (4.62), (4.63) следует, что
 |
(4.65) |
аналогично, то есть путем вычитания, из (4.24) и (4.25) уравнений соответственно (4.34) и (4.35) получаем
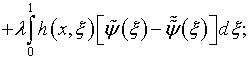
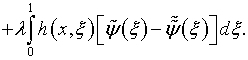
В результате вычитания, с использованием (4.65), возникают однородные уравнения:
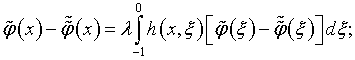
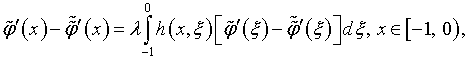
решения которых при условии (4.18)
– тривиальны. Таким образом, соотношения (4.62),
(4.63) автоматически влекут
за собой тождества (4.64).
Иначе говоря, из существования указанных соотношений следует, что функции
и
в уравнениях соответственно (4.24),
(4.34) и (4.25),
(4.35) одни и те же.
Процедура вычитания в каждой из этих пар уравнений дает
и с помощью замены переменных
получаем
Это однородное интегральное уравнение Фредгольма первого рода с ядром (4.11). На основании его замкнутости, можно сделать вывод о том, что
Следовательно, для того, чтобы функции 
определяемые по формулам (4.30),
(4.31), удовлетворяли
уравнениям как (4.25),
так и (4.35), а значит
также их разности, являющейся уравнением (4.1),
функция
должна представлять собой решение интегрального уравнения Фредгольма второго
рода (4.52). Это очень
важный момент всего изложения.
Заметим, что использование вместо (4.64) одного лишь тождества
возможно, однако интегральное
уравнение Фредгольма второго рода, получаемое путем подстановки выражения (4.63)
в (4.61), было бы более
громоздким.
Начиная с п.4.2 и вплоть до настоящего момента изложения предполагалось,
что функция
удовлетворяющая уравнению (4.1),
может быть только гармонической; соответственно его свободный член
определяется выражением (4.22).
Здесь приводится обобщение алгоритма п.4.4, для чего будет использован подход,
аналогичный суммированию рядов Фурье методом Абеля-Пуассона [2,
3]:
- проведение
преобразований в аналитическом виде с гармонической функцией 
которая представима хорошо сходящимся рядом, при 
в (4.19);
- предельный переход в
выражении через
данные задачи, представляющем ряд, члены которого явно зависят от параметра
Таким образом, будет получено решение задачи, сформулированной
в п.4.1. То есть, – восстановлена
-функция
на основании результата ее интегрирования по формуле (4.1),
или же близкого к нему выражения 
которое является данным.
В уравнении (4.40) представим
 |
(4.66) |
где 
и
–
неопределенные коэффициенты;
 |
(4.67) |
 |
(4.68) |
где коэффициенты Фурье
 |
(4.69) |
(заметим, что вычисление этих функций не потребуется);
 |
(4.70) |
Соответственно
 |
(4.71) |
 |
(4.72) |
Подстановка
выражений (4.66) – (4.68)
в уравнение (4.40) и приведение
множителей при 
сводят вычисление коэффициентов 
к решению системы линейных алгебраических уравнений:
 |
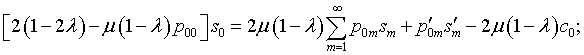
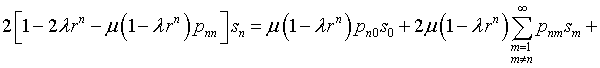
(4.73) |
где с учетом (4.69)
 |
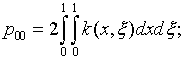
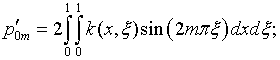
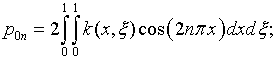
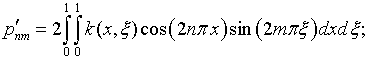
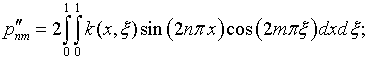
(4.74) |
Очевидно,
для разрешимости системы уравнений (4.73)
параметр
должен быть таким, чтобы, как и в п.4.4, решение уравнения (4.60)
могло быть только тривиальным. Заметим, что при 
то есть в случае, когда условие (4.18)
не выполняется, элементы столбца свободных членов (4.73)
обращаются в нуль.
В выражении (4.41)
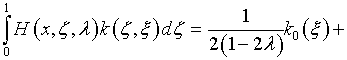
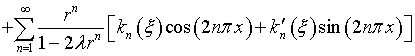
и соответственно
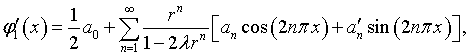
где
 |
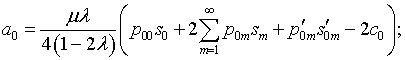
(4.75) |
Подстановка
этой функции в (4.54)
и затем 
– в (4.57) приводит к
выражению
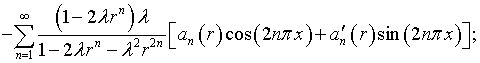
в результате по формуле (4.30) получаем
 |
(4.76) |
где
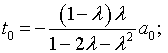
Предельный
переход
дает следующие коэффициенты ряда (4.76):
 |
(4.77) |
где с учетом (4.75)
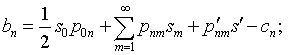
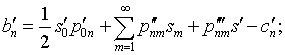
– константа. При этом
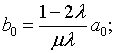
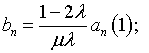
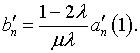
В качестве примера, поясняющего механизм производимых выкладок, рассмотрим определение функций (4.54) и (4.30):
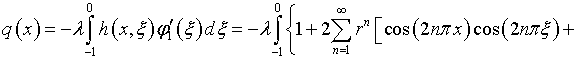
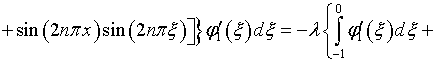
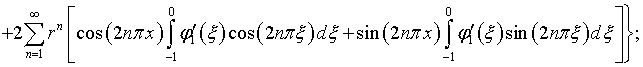
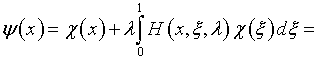
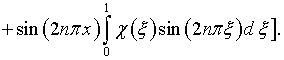
Здесь
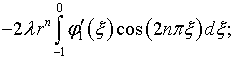
и
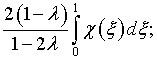
– коэффициенты Фурье функций соответственно и
То
есть, при в первом
случае происходит пересчет с множителем 
коэффициентов
Фурье ( и
определены
соответственно на 
и
);
во втором – функция выражается
через путем
обыкновенного умножения на 
Система
линейных алгебраических уравнений (4.73)
при 
принимает вид:
 |
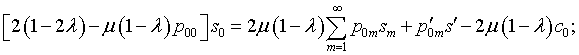
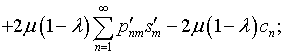
(4.78) |
Элементы
ее матрицы преобладают на диагонали, за счет компоненты 
не зависящей от 
и 
вследствие чего для определения коэффициентов 
содержащихся в (4.66),
эффективны разнообразные методы [9].
Если
и
представляют собой
-функции, отвечающие им ряды Фурье (4.67),
(4.68), сходятся в среднем.
Из (4.71) и (4.72)
при 
 |
(4.79) |
содержащиеся здесь множители ограничены, следовательно, аналогичным образом сходятся и ряды, получаемые в результате подстановки выражений (4.67), (4.68).
Условие разрешимости системы уравнений (4.78)
эквивалентно отсутствию нетривиальных решений уравнения (4.60)
с ядром и свободным членом (4.79).
Одновременно класс функций, в котором может находиться решение интегрального
уравнения Фредгольма второго рода (4.40),
расширяется до пространства
Соответственно
ряд (4.66), приближающий
функцию 
сходится в среднем и согласно равенству Парсеваля
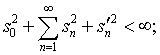
из (4.77) следует, что таким же образом сходится и ряд (4.76):
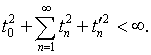
На
основании теоремы Рисса-Фишера [1]
и предшествовавших выкладок, можно сделать вывод о том, что он представляет
собой разложение
-функции
удовлетворяющей уравнению (4.1),
в ряд Фурье по элементам 
Следует
отметить, параметр сыграл
здесь исключительно важную роль, поскольку без него оказалось бы невозможным:
- собственно, построение алгоритма, приведшего к уравнениям (4.40) и (4.52);
- выполнение
преобразований с интегралами, ядра которых имеют вид рядов (4.19),
(4.21), (4.55)
и (4.56), расходящихся
при 
Итак,
значения 
и 
в (4.76) определяются
через коэффициенты Фурье данных задачи посредством устойчивой процедуры численной
реализации, которая включает этапы:
- установление параметра
из условий (4.59) при
то есть
- установление параметра
так, чтобы решение уравнения (4.60)
с данными (4.79) могло
быть только тривиальным;
- вычисление
коэффициентов 
и 
по формулам соответственно (4.70)
и (4.74);
- определение
коэффициентов 
и
из системы линейных алгебраических уравнений (4.78);
- вычисление коэффициентов
и
по формулам (4.77).
Удовлетворение условия (4.6), после подстановки в (4.8) выражений (4.76), с коэффициентами (4.77), и
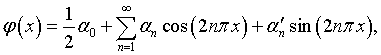
сводится к пересчету коэффициентов Фурье:
 |
(4.80) |
соответственно предельный переход по 
превращает в
-функцию также и 
Условие (4.6) подразумевается
теперь в смысле
 |
(4.81) |
Таким
образом, при 
могут быть найдены коэффициенты Фурье функции
позволяющие удовлетворить условие (4.81).
Однако эта же дискретизация изначально, то есть без преобразований с параметром
о чем уже упоминалось, полностью исключила бы возможность построения алгоритма,
позволяющего определить функцию
которая удовлетворяет уравнению (4.1).
При
в него превращается выражение (4.22);
с учетом (4.80) и (4.76).
Соответственно, прекращает действовать ограничение на вид свободного члена
которое налагал «гармонический» случай решения задачи.
Существенно
отметить, вывод п.4.5, о том, что функция
действительно удовлетворяет уравнению (4.1),
при
остается в силе. Соотношение (4.61)
выполняется в этом случае аналогично (4.81),
то есть посредством зависимости между коэффициентами Фурье функций
и
В
п.5.3 будет изложен метод решения задачи (4.1)
без предельного перехода по параметру
Это достигается за счет удовлетворения условию (4.6)
в смысле обобщенных функций. Общая направленность выкладок остается неизменной,
в полной мере используются результаты п.4.4.
