|
|
|
|
|
Итак, считаем, что ядро 
интегрального уравнения Фредгольма первого
рода (3.1) симметрично, замкнуто и функция 
удовлетворяющая ему в 
существует. Соответственно 
то есть выполняется условие [13]:
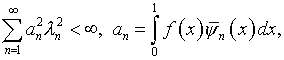(3.4)
где 
– характеристические числа
и собственные функции ядра 
Заметим также, что система элементов
полна в 
или же пространстве 
[33, с.69].
В таком случае оператор 
осуществляющий отображение из пространства
в – ограничен (теорема Банаха).
Получается, определение функции 
по формуле (3.2) можно произвести
без накопления погрешности?
С этой точки зрения, «Обратимый мир Банаха» исключительно заманчив, однако
в нем отсутствует какая-либо дифференциация используемых пространств по предпочтительности.
Они определяются содержанием задачи, то есть оператором 
Главенствующие тенденции
в сфере вычислительной математики – сугубо альтернативны, из-за чего как явно,
так и, преимущественно, исподволь проводится тезис о фактической бесполезности
теоремы Банаха об обратном операторе.
На первый взгляд, для этого имеются веские основания. Действительно, малость
возмущения данных, а также и погрешности, допускаемой при проведении вычислительных
операций, подразумевается в 
Однако практическая возможность для выполнения
такого условия – отсутствует. Пространство как бы иллюзорно, поскольку оперирует с бесконечной
совокупностью признаков данных задачи, становящихся при больших значениях 
в (3.2) по существу – неидентифицируемыми.
Можно заметить также, что уравнение (3.1) является в определенном смысле
– нелинейным. В самом деле, представим интегрируемую по формуле (3.1) функцию
Соответственно
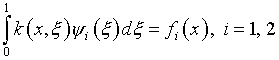
и каждое из этих уравнений разрешимо в смысле выполнения условия вида (3.4).
Однако функцию 
можно представить суммой бесконечного набора
слагаемых. Если предположить, что уравнения
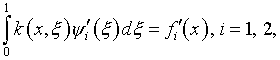
где 
при произвольном разделении
на 
и 
– разрешимы, приходим к противоречию. Действительно,
решение уравнения (3.1) – единственно и условие вида (3.4) выполняется лишь
для 
Таким образом, принцип линейной суперпозиции в отношении свободного члена уравнения (3.1) не работает.*
|
* Отмеченный момент отчасти пересекается с изложением
п.6.5.
|
Данное обстоятельство обуславливается незамкнутостью области значений оператора
о которой упоминалось в п.1.3.
В общем, получается, что теоретическая принадлежность
функции 
пространству – реально ничего не дает.
Вместе с тем, подобный вывод не может служить основанием для игнорирования пространства
при рассмотрении задачи (3.1). Как представляется,
конструктивизм здесь возможен исключительно в контексте согласования, вообще
говоря, альтернативных устремлений:
-
функция 
используемая при проведении вычислений, принадлежит
пространству 
-
оператор 
осуществляет отображение из 
в пространство
Мотивация очевидна, – сохранить потенциал непрерывной обратимости оператора
в целях его практической реализации. Вместе
с тем обозначенное противоречие налицо и преодолеть его, ограничиваясь исключительно
рамками интегрального уравнения Фредгольма первого рода (3.1), не представляется
возможным. В подобной ситуации естественно обратиться к, образно выражаясь,
происхождению данного уравнения, то есть – к постановке задачи.
Итак, имеется явление, описываемое оператором Прямая задача состоит в вычислении
интеграла по формуле (3.1) при подстановке в нее функции 
Такая процедура обладает множеством интерпретаций
и математически корректна.
Ключевой момент – формулировка обратной задачи для того же оператора 
которая сопряжена с восстановлением
функции по реализации упомянутого интегрирования,
то есть – 
Соответственно подразумевается определение
причины по следствию, и если постановка прямой задачи наглядна, то в отношении
обратной ситуация – прямо противоположная. При ее разрешении приоритетной становится
собственно алгоритмическая процедура (на базе адекватной математической модели),
не являющаяся аналогом процесса, проистекающего в режиме реального времени.*
|
*
Действительно, порождение следствием причины, как процесс, – не имеет
физического смысла.
|
Как в свете изложенного не обратиться к утверждению Адамара о том, что все
задачи, имеющие практическое истолкование, допускают
математически корректную постановку? Исходя из этого, поскольку функция в (3.1) объективно существует,
задачу ее определения следует всего лишь адекватно сформулировать. Вместе с
тем, Адамар не привел соответствующих рекомендаций практического характера,
и, как уже отмечалось, его методология оказалась фактически отвергнутой.
Однако попытаемся наметить постановку задачи, обратной вычислению интеграла (3.1), которое в общем случае производится с некоторой погрешностью:
(3.5)
В прямой постановке ее учет не имеет принципиального значения, однако, решения
интегральных уравнений Фредгольма первого рода (3.1) и (3.5) могут оказаться
совершенно разными. При этом ставить вопрос о какой-либо количественной оценке
– бессмысленно. Можно считать лишь, что по
сравнению со значениями функций 
и погрешность является малой.
Из общих соображений, присутствие в (3.5) повышает потенциал постановки обратной задачи,
наряду с чем, возникает вопрос о функциональном представлении погрешности. В
этой связи следует принять во внимание, что механизм ее генерации обуславливается
фактором сглаживания процедурой интегрирования,
а значит, структура должна отражать данное обстоятельство.
В ракурсе сказанного, воспользуемся операторной моделью погрешности вида
(3.6)
где 
– тождественный оператор;
– некоторый интегральный оператор; 
и 
– параметры.
Итак, вместо уравнения (3.1) предлагается иметь дело со следующей задачей:
(3.7)
преследуя целью
сведение ее к решению интегрального уравнения Фредгольма второго рода. Параметр
как и при обращении оператора
предназначен для того, чтобы это уравнение
не располагалось на спектре, что эквивалентно существованию и единственности
его решения.
Обратим внимание, к свободному члену уравнения (3.1) всего лишь прибавлена
функция, представляющая «нуль». Вместе с тем, переход от некорректной задачи
(3.1) к постановке (3.6) создает предпосылки для кардинального изменения ситуации.
От 
вообще говоря, можно потребовать адаптивной
компенсации погрешности вычислительных операций, выводящих из пространства 
вследствие чего появляется перспектива реализации
ограниченного оператора 
В самом деле, при 
негативный фактор некорректности уравнения
(3.1) – нивелируется.
Предположим, что оператор из (3.6), при котором 
в пространствах 
или 
окажется возможным представить
в виде
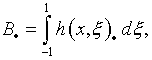
с наложением на
ядро 
определенных условий. В таком случае задача
(3.7) становится следующей:
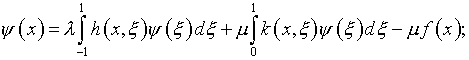(3.8)
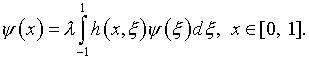(3.9)
Таким образом, равенство нулю эквивалентное уравнению (3.9), предполагается
удовлетворить с помощью на 
– новой неизвестной функции.
Бытует суждение будто бы перспективы получения весомых результатов с помощью простых преобразований математических зависимостей – невелики. В самом деле, применив к уравнениям (3.8), (3.9) операцию вычитания, вновь получим исходную задачу (3.1), которая некорректна. Однако, во-первых, мы не собираемся этого делать и, во-вторых, за интегральными уравнениями с искомой функцией в явном виде интуитивно ощутим конструктивный потенциал.
С этой точки зрения, весьма знаменательным можно назвать «несрабатывание»
примера, иллюстрирующего сглаживание информации о функции процедурой интегрирования (3.1),
который приведен в целом ряде изданий. Действительно, предполагая, что функция
удовлетворяющая системе уравнений (3.8), (3.9),
известна, сообщим ей возмущение вида 
Подстановка в (3.7) показывает,
что на свободный член оно будет влиять как с понижающим коэффициентом
(сглаживание), так и без него – за счет соответственно интегральной компоненты
и функции в явном виде.
Сказанное не распространяется на 
однако определение этой
функции выходит за рамки рассматриваемой задачи. Подчеркнем, что последние соображения
– исключительно наводящего характера.
С позиций практической реализации изложенного, весьма существенной представляется
взаимосвязь пространств 
а также и Как известно, в паре пространств
и 
она – теснейшая. Теорема
Рисса-Фишера [34] устанавливает взаимнооднозначное, непрерывное и линейное соответствие
между функциями из и числовыми последовательностями
со сходящейся суммой квадратов. То есть, всегда
существует -функция, для которой
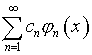
является рядом
Фурье по системе ортонормированных элементов 
Однако между пространствами и а соответственно и также наблюдается весьма интересная зависимость.
Действительно, (3.2) представляет собой ряд Фурье по ортонормированным элементам
условием сходимости которого является (3.4).
Если предположить, что 
где 
то при 
пространство превращается в 
Вместе с тем, ядро в (3.1) обладает характеристическими числами,
которые ему объективно присущи, и, следовательно, использоваться для такого
превращения не может. Но появилось не зависящее от данных задачи ядро 
а с ним и перспектива реализации намеченного
замысла. Ниже вокруг этого момента будет сосредоточена значительная часть всего
изложения.
В заключение настоящего раздела хотелось бы отметить спорность распространенного мнения о необходимости формулировки задач математического моделирования специалистами-прикладниками соответствующего профиля, тогда как предназначение математиков состоит в проведении строгих аналитических исследований, разработке вычислительных методов и участии в их реализации.
Как представляется, прикладники должны заниматься постановкой прямых и в целом корректных задач. Фактор некорректности тесно взаимосвязан с процедурой численной реализации, вследствие чего уделом математиков является приведение постановок задач, описывающих изучаемые процессы и явления, к условиям применимости теоремы Банаха об обратном операторе.
