|
|
|
|
|
Следуя сказанному в п.3.5,
выразим погрешность вычисления 
по формуле (4.1) разностью искомой функции
и интегральной компоненты:
(4.4)
где 
– постоянная; оператор
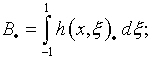(4.5)
о ядре 
будет сказано ниже.
Однако предполагается
построение устойчивого алгоритма вычисления функции 
удовлетворяющей уравнению (4.1),
и, следовательно, малые вариации данных не должны существенно влиять на решение.
В этой связи рассмотрим возможность выполнить условие
(4.6)
допуская, тем самым, что конструктивно разрешить задачу, сформулированную в
п.4.1, удастся с помощью (всего лишь) прибавления к свободному члену уравнения
(4.1) «нуля» из (4.4), имеющего следующий вид:*
|
* Здесь погрешность
 или же зависящая от нее
функция, трактуются в качестве составляющей свободного члена интегрального
уравнения Фредгольма второго рода, посредством решения которого будет
находится  |
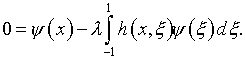
Это уравнение можно представить так:
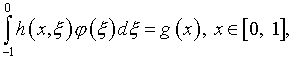(4.7)
где
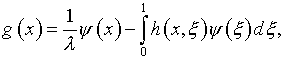(4.8)
и с помощью замены переменных
(4.9)
привести к каноническому виду
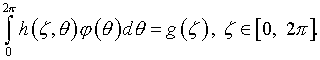(4.10)
Очевидно, выполнение условия
(4.6) эквивалентно разрешимости этого уравнения. Пусть ядро 
принадлежит пространству
и замкнуто. В таком случае (4.10) является
интегральным уравнением Фредгольма первого рода, решение которого, если оно
существует, единственно [1]. Удовлетворяя указанные требования, представим (4.10)
в виде интеграла Пуассона [2, с. 202-205]. Соответственно ядро
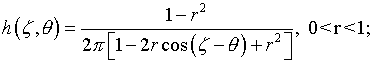(4.11)
его характеристические числа и ортонормированные на 
собственные функции [1, с.187-188]:
|
|
|
|
при этом в (4.7)
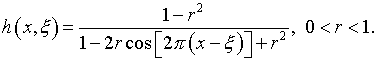(4.13)
Если в уравнении (4.10) функция
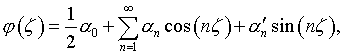(4.14)
где 
и 
– коэффициенты ее разложения
в ряд Фурье, абсолютно интегрируема, то есть
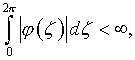
функция
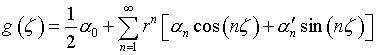(4.15)
представляет собой действительную часть аналитической внутри единичного круга
функции и является гармонической [3, с.160-161; 4]:
где 
– декартовы координаты.*
* Здесь
параметр  рассматривается в качестве радиальной координаты;
соответственно  – полярный угол. |
Поскольку указанное свойство
не зависит от линейной замены переменных, из (4.8) с учетом (4.9) и (4.15) следует,
что при условии (4.6) функция удовлетворяющая уравнению (4.1), может быть
только гармонической. То есть, – принадлежащей классу функций, значительно более
узкому, нежели предполагалось постановкой задачи в п.4.1.
И все же, можно сделать
вывод о том, что «нулевая» погрешность интегрирования гармонической функции
по формуле (4.1) действительно
представима в виде (4.4) при ядре из (4.13). Это важный момент
изложения.
Компоненты (4.12) удовлетворяют однородному уравнению
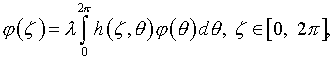
которое путем замены переменных
преобразуется следующим образом:
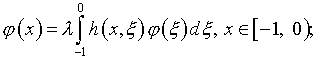
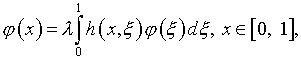(4.16)
позволяя, с учетом также (4.12), (4.9), определить характеристические числа
и ортонормированные на 
собственные функции ядра
(4.13):
|
|
(4.17) |
|
|
Решение задачи (4.1) является
единственным. Соответственно из сопоставления однородного интегрального уравнения
Фредгольма второго рода относительно отвечающего (4.8) (то есть
при 
), и (4.16) вытекает условие:
(4.18)
Так как ядро в (4.16)
симметрично, непрерывно и все 
то на основании теоремы Мерсера [1]
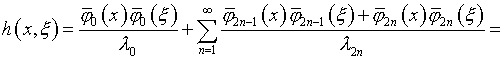
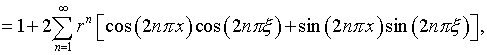(4.19)
причем этот ряд сходится абсолютно и равномерно.
Далее потребуется резольвента
оператора 
Из билинейного разложения (4.19), при использовании
той же теоремы Мерсера, следует, что характеристические числа и ортонормированные
на 
собственные функции его ядра имеют вид
|
|
|
|
|
а значит необходимо поставить еще одно условие:
(4.20)
Следует принять во внимание,
что использование теоремы Мерсера явилось отличным от предшествовавшего представления
ядра рядом (4.19). Здесь, напротив, существует
разложение ядра в равномерно сходящийся билинейный ряд по
ортогональной на 
системе элементов. Соответственно, эти элементы,
с поправкой на нормирующий множитель, и значения 
представляют собой собственные функции и характеристические
числа оператора
Заметим также, что функции
ортогональны не только
на 
но и на 
Данное обстоятельство
сыграет ниже весьма важную роль в плане упрощения процедуры численной реализации.
Резольвента ядра (4.5) определяется рядом [1]:
|
|
|
|
|
(4.21) |
который при условии (4.20) также сходится абсолютно и равномерно.
Из (4.8) и (4.15), с учетом (4.9),
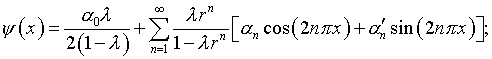
таким образом, при условии (4.6) уравнение (4.1) может быть удовлетворено лишь
в случае, когда
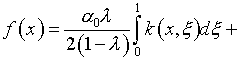
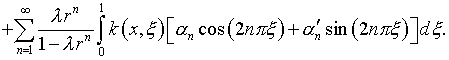(4.22)
При проведении последующих
выкладок предполагается, что функция 
– гармоническая и свободный член уравнения
(4.1) имеет вид (4.22). Данное обстоятельство, о чем уже упоминалось, резко
сужает круг практических приложений. Как будет показано (п.4.6), полученное
для такого случая решение путем предельного перехода 
превращается в -функцию которая удовлетворяет уравнению
(4.1).*
| * Одновременно (4.22) приобретает вид (4.1). |
