ВВЕДЕНИЕ
Вначале следует пояснить название работы и в первую
очередь смысл использованных понятий. В этой связи предположим
наличие информации, позволяющей традиционным путем сформулировать
математическую модель некоторого явления. Соответственно подразумевается
определение неизвестных функций по данным задачи. Если зависимость
решения от них в норме выбранного пространства непрерывна, то,
как правило, такая задача относится к сфере анализа, или же ее
постановка является прямой.
Однако исследование конкретного явления во всей
совокупности определяющих его факторов с целью получения в итоге
качественно новой информации (синтез знаний) предусматривает также
и реализацию задач в обратной постановке, то есть восстановление
данных по гипотетически известному решению. Иначе говоря, – причины
по следствию, что принято отождествлять с необходимостью разрешения
некорректно поставленной задачи.
Цель настоящего исследования состоит в обосновании
неправомерности подобного суждения и, напротив, конструктивном
развитии воззрений Ж.Адамара о существовании корректных постановок
задач, адекватно описывающих реальные процессы и явления. Заметим,
что различие между последними из указанных понятий при их упоминании
в тексте – непринципиально и вместе с тем “процесс” как бы акцентирует
временной фактор.
В центре внимания вполне закономерный, по нашему
мнению, вопрос, который целесообразно пояснить на примере вычисления
интеграла
 ,
(1)
,
(1)
то есть, определении функции  по данным
по данным 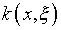 и
и  .
Этой процедуре нетрудно поставить в соответствие множество физических,
а также иных интерпретаций; ее реализация, во всяком случае когда
подынтегральное выражение ограничено, не вызывает затруднений.
.
Этой процедуре нетрудно поставить в соответствие множество физических,
а также иных интерпретаций; ее реализация, во всяком случае когда
подынтегральное выражение ограничено, не вызывает затруднений.
С другой стороны, если ядро 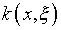 и правая часть
и правая часть  вычисленная как указано по формуле (1), заданы, то очевидно, что
отвечающая им функция
вычисленная как указано по формуле (1), заданы, то очевидно, что
отвечающая им функция  объективно существует. Итак, вопрос: правомерно ли восстанавливать
эту функцию посредством решения интегрального уравнения Фредгольма
первого рода (1), вытекающего из оговоренной прямой задачи, всего
лишь переименовав известный и неизвестный компоненты. То есть,
полагая что функция
объективно существует. Итак, вопрос: правомерно ли восстанавливать
эту функцию посредством решения интегрального уравнения Фредгольма
первого рода (1), вытекающего из оговоренной прямой задачи, всего
лишь переименовав известный и неизвестный компоненты. То есть,
полагая что функция  – задана, а
– задана, а  – подлежит определению. И, вообще говоря, на основании чего математические
выражения обратной и прямой задач могут быть совершенно идентичны?
– подлежит определению. И, вообще говоря, на основании чего математические
выражения обратной и прямой задач могут быть совершенно идентичны?
Кстати, очень сложно представить способ постановки
обратной задачи из физических соображений – непосредственно, вне
привязки к соответствующей прямой. Вызывает протест собственно
факт примитивного переименования известных и неизвестных функций
без внесения каких-либо дополнительных корректив. Итак, выдвигается
тезис о том, что конструктивный подход к формулировке обратных
задач должен отличаться от ставшего общепринятым. Такая направленность
обусловила присутствие в названии работы понятия методологии.
По существу мы надеемся изыскать резервы синтезирования
всего комплекса знаний о явлении, исследуя его с разных сторон
в постановках, математические выражения которых нетождественны.
Если для вычисления  формула (1) в полной мере оправдана, то задача восстановления
функции
формула (1) в полной мере оправдана, то задача восстановления
функции  совсем не обязательно должна совпадать с ней по своему представлению
и соответственно сводиться к интегральному уравнению Фредгольма
первого рода, характеризующемуся неустойчивостью алгоритмов численной
реализации.
совсем не обязательно должна совпадать с ней по своему представлению
и соответственно сводиться к интегральному уравнению Фредгольма
первого рода, характеризующемуся неустойчивостью алгоритмов численной
реализации.
Но если имеется альтернатива формулировке обратных
задач путем отмеченного переименования известных и неизвестных
компонентов, логично предположить, что соответствующие постановки
могут обладать гораздо более привлекательными в вычислительном
отношении свойствами. С этой точки зрения доводы Ж.Адамара приобретают
вполне конкретный смысл, стимулируя поиск адекватных существу
рассматриваемых ситуаций и одновременно корректных постановок
задач математической физики. Конструктивная реализация обозначенной
направленности оказалась возможной в контексте следующих соображений.
Причины осложнений, связанных с решением некорректно
поставленных, а по существу не имеющих математического смысла
задач, в принципе хорошо осознаны. Применительно к интегральному
уравнению Фредгольма первого рода (1) главную роль играет рассогласованность
между функцией 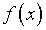 и гипотетически точным решением соответствующей прямой задачи
(результат интегрирования) в условиях аппроксимаций, а также различных
округлений значащих цифр.
и гипотетически точным решением соответствующей прямой задачи
(результат интегрирования) в условиях аппроксимаций, а также различных
округлений значащих цифр.
Соответственно большое внимание уделяется так
называемому феномену сглаживания информации в процедурах интегрирования.
Вместе с тем данные задачи, то есть свободный член 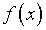 ,
а также и ядро
,
а также и ядро 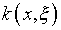 зачастую определяются экспериментально, вследствие чего в уравнение
(1) заведомо вносится существенная погрешность. В этой связи отметим
доминирование методологии А.Н.Тихонова, которая исходит из объективной
некорректности постановок большей части задач математического
моделирования.
зачастую определяются экспериментально, вследствие чего в уравнение
(1) заведомо вносится существенная погрешность. В этой связи отметим
доминирование методологии А.Н.Тихонова, которая исходит из объективной
некорректности постановок большей части задач математического
моделирования.
Возникает достаточно очевидный, как представляется,
вопрос: почему бы не только иметь в виду на уровне идентификации
причин вычислительных недоразумений, но и практически учитывать
упомянутые погрешности при формулировке задач? Можно предположить,
что адекватное моделирование погрешности будет способствовать
корректной постановке задач, считающихся обратными.
Адекватность подразумевает прежде всего структуру
представления погрешности, в связи с чем обратимся к процедуре
интегрирования (1). Из общих соображений, потерю информации о
функции  при вычислении
при вычислении 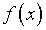 логично изобразить в виде
логично изобразить в виде
 (2)
(2)
Здесь к функции  ,
xÎ [-1, 0), ядру
,
xÎ [-1, 0), ядру  и параметру l предъявляется требование реализации условия
вида
и параметру l предъявляется требование реализации условия
вида  в
в 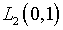 для
для  из достаточно представительного класса. Как будет показано, существенных
затруднений при этом не возникает.
из достаточно представительного класса. Как будет показано, существенных
затруднений при этом не возникает.
Таким образом, намеченная структура олицетворяет
разность между подлежащей интегрированию функцией  и близким к ней выражением, которое, в свою очередь, является
результатом выполнения аналогичной процедуры. Следует подчеркнуть
отсутствие каких-либо априорных предпосылок самодостаточности
(2) для достижения преследуемой цели, а именно – корректной постановки
задачи о восстановлении функции
и близким к ней выражением, которое, в свою очередь, является
результатом выполнения аналогичной процедуры. Следует подчеркнуть
отсутствие каких-либо априорных предпосылок самодостаточности
(2) для достижения преследуемой цели, а именно – корректной постановки
задачи о восстановлении функции  по данным (1). То есть, мы как бы выдвинули гипотезу о приоритетной
значимости качественной стороны модели сглаживания информации.
по данным (1). То есть, мы как бы выдвинули гипотезу о приоритетной
значимости качественной стороны модели сглаживания информации.
В свете изложенного, вместо традиционной некорректно
поставленной задачи (1) для определения функции  использована следующая система уравнений:
использована следующая система уравнений:

где m – параметр, аналогичный l
.
В результате сравнительно несложных преобразований
рассматриваемую задачу удалось свести к решению интегрального
уравнения Фредгольма второго рода с наиболее благоприятными для
численной реализации свойствами. Подразумевается отсутствие особенностей,
а также осцилляций ядра, не обусловленных 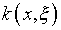 ,
то есть, таких, которые навязывал бы применяемый алгоритм.
,
то есть, таких, которые навязывал бы применяемый алгоритм.
При этом наряду с явным присутствием искомой функции
и в целом структурой представления погрешности (2), необходимым
условием явилась полнота ядра
 ,
,
а упрощение выкладок оказалось возможным за счет
его симметрии:  и зависимости от разности аргументов.
и зависимости от разности аргументов.
Однако, к интегральным уравнениям Фредгольма первого
рода вполне элементарно редуцируются широкие классы линейных краевых
и начально-краевых задач математической физики, вследствие чего
оговоренная процедура может рассматриваться в качестве эффективного
метода их численной реализации. Настоящее утверждение иллюстрирует
пример:
 ,
x = y = 0; x = y = 1. (3)
,
x = y = 0; x = y = 1. (3)
Из обозначения  c учетом (3) следует
c учетом (3) следует
 (4)
(4)
 (5)
(5)
Исключение функции  приводит к двумерному интегральному уравнению Фредгольма первого
рода. В случае условий на контуре более общего вида может использоваться,
например, следующее соотношение:
приводит к двумерному интегральному уравнению Фредгольма первого
рода. В случае условий на контуре более общего вида может использоваться,
например, следующее соотношение:  Намеченная схема практически индифферентна к типу и порядку дифференциальных
операторов, наличию переменных коэффициентов, конфигурации границ
области определения и ряду других факторов, как правило, осложняющих
реализацию вычислительных алгоритмов.
Намеченная схема практически индифферентна к типу и порядку дифференциальных
операторов, наличию переменных коэффициентов, конфигурации границ
области определения и ряду других факторов, как правило, осложняющих
реализацию вычислительных алгоритмов.
Заметим, что размерность краевой задачи в плане
последующего сведения к интегральному уравнению Фредгольма второго
рода не принципиальна, поскольку фактически данная процедура осуществляется
по одной из переменных, тогда как остальные выступают в роли своеобразных
параметров. И, кстати, в обозначенном ракурсе используемая дифференциация
задач математического моделирования на прямые и обратные становится
достаточно условной.
Нелинейные краевые и начально-краевые задачи в
целом аналогично сводятся к нелинейным интегральным уравнениям
второго рода, которые специальным образом адаптированы для эффективной
реализации итерационных алгоритмов.
Возможно, определенный интерес представит мотивация
предлагаемого исследования. Изначально у автора возникло недоумение
из-за отсутствия в специальной литературе четкой констатации универсальности
показанного приема редукции задач математической физики к интегральным
уравнениям Фредгольма первого рода. При всей сложности разрешения
некорректных задач, фактор исключения граничных и начальных условий,
а также погружение всего сонмища исходной информации в ядра получаемых
уравнений представляются все же весьма привлекательными. В самом
деле, фактически стирается устоявшаяся ранжировка классов задач
по трудоемкости их численной реализации и на первый план выходит
построение эффективного алгоритма решения интегрального уравнения
Фредгольма первого рода.
Вместе с тем обращает внимание своеобразная вырожденность
соотношения для новой неизвестной y , порождающего
представления (4), (5). Возникает естественный вопрос: имеется
ли возможность приведения краевых задач к уравнениям с более приемлемыми
в смысле численной реализации свойствами посредством зависимости
между функциями u и y более общего вида. Например,
полагая

где

доопределить ядро  так, чтобы задача (3) обратилась в интегральное уравнение Фредгольма
второго рода относительно функции y? Однако осуществить
что-либо подобное не удалось.
так, чтобы задача (3) обратилась в интегральное уравнение Фредгольма
второго рода относительно функции y? Однако осуществить
что-либо подобное не удалось.
Также безрезультатно завершились попытки сведения
рассматриваемых задач к интегральным уравнениям первого рода  в которых оператор В имел бы подходящую формулу обращения
(A и f аналогично (1) характеризуют данные конкретного
явления). Вместе с тем из этого никак не следовало, что алгоритм
получения в итоге преобразований интегрального уравнения Фредгольма
второго рода – принципиально нереализуем.
в которых оператор В имел бы подходящую формулу обращения
(A и f аналогично (1) характеризуют данные конкретного
явления). Вместе с тем из этого никак не следовало, что алгоритм
получения в итоге преобразований интегрального уравнения Фредгольма
второго рода – принципиально нереализуем.
Конструктивным оказалось использование модели
сглаживания информации процедурой интегрирования вида (2). В этой
связи потребовалась углубленная проработка методологических аспектов
корректной постановки задач математической физики.
В первом разделе проанализированы соображения
Ж.Адамара по проблематике корректной постановки задач для дифференциальных
уравнений с частными производными. Освещены также коррелирующие
с ними и альтернативные позиции известных специалистов. Приведены
различные трактовки близкой по содержанию теоремы Банаха об обратном
операторе – одного из трех основных принципов функционального
анализа.
Второй раздел содержит критический обзор методов
решения некорректных задач, базирующихся в первую очередь на концепциях
А.Н.Тихонова и В.М.Фридмана. Высказаны соображения о причинах
кризиса в сфере математического моделирования, сопряженного с
ориентацией на использование некорректных постановок, сводящихся
к численной реализации плохо обусловленных алгебраических систем.
Материал третьего раздела как бы преломляет принципиальные
осложнения, возникающие при решении некорректно поставленных задач,
сквозь призму фундаментальных положений Ж.Адамара и С.Банаха.
В контексте изложения сформулированы общие предпосылки корректной
постановки задач математического моделирования, традиционно ассоциируемых
с интегральными уравнениями Фредгольма первого рода.
Четвертый раздел посвящен изложению оригинального
подхода к решению канонического уравнения указанного типа и является
в конструктивном отношении базовым. Здесь исследованы вопросы,
связанные с моделированием погрешности и трансформацией исходной
постановки, приведен алгоритм сведения задачи к интегральному
уравнению Фредгольма второго рода, а также рассмотрены соответствующие
аспекты методологического характера.
В пятом разделе предметно продемонстрирована универсальность
приема редукции линейных краевых и начально-краевых задач к интегральным
уравнениям Фредгольма первого рода относительно одной из старших
производных. Показано также распространение на них алгоритма предыдущего
раздела.
Шестой раздел развивает обозначенную направленность,
вовлекая в сферу эффективной реализации достаточно нетривиальные
приложения (с учетом факторов нелинейности, сингулярного возмущения
и ряда других). Форма изложения материала носит характер эскизных
зарисовок.
В заключении подытожены основные положения предлагаемого
исследования с позиций приоритетной значимости корректной постановки
задач математического моделирования для их численной реализации.
Математический аппарат, использованный при изложении
материала, сравнительно несложен: положения классической теории
интегральных уравнений; элементы функционального анализа; общие
представления о постановках задач математической физики и методах
их решения.
Литературные источники указаны к каждому из разделов
в порядке ссылок. Главным образом, содержатся не оригинальные
издания, а работы, в которых тот или иной вопрос изложен наиболее
обстоятельно. Разделы и подразделы (главы и параграфы библиографических
источников) обозначены соответственно: п.1, п.1.1, пп.1.1, 1.2.
Нумерация формул в основном тексте двойная: первая
цифра указывает раздел, вторая – порядковый номер в разделе. Нумерация
формул во введении и заключении – одинарная. Ссылки на формулы
преимущественно замыкаются внутри разделов.
По тематике работы имеется около 30 авторских
публикаций, включая центральные периодические издания и труды
представительных симпозиумов. Все публикации – самостоятельные.
В них вполне четко обозначена общая направленность исследования,
а также средства ее практической реализации, однако лишь обратившись
к методологии корректной постановки задач математической физики
оказалось возможным изложить обоснование разработанного подхода.
Формированию нашедших отражение ниже концепций
на разных этапах способствовало общение с целым рядом известных
специалистов: профессора С.М.Белоносов, П.М.Варвак, Э.С.Венцель,
Н.А.Вирченко, Ю.В.Гандель, Ю.А.Данилов, В.А.Добрушкин, М.Д.Дольберг,
Н.Т.Жадрасинов, П.А.Жилин, Б.Я.Кантор, В.В.Копасенко, К.А.Лурье,
С.Г.Михлин, Н.Ф.Морозов, М.В.Паукшто, А.С.Сахаров, Э.А.Симсон,
В.С.Рябенький, Л.А.Фильштинский, Н.П.Флейшман, Д.Г.Хлебников,
А.В.Черкаев, И.Ю.Чудинович, И.Д.Чуешов, В.А.Щербина, а также член-корреспондент
АН СССР А.И.Лурье, академик НАН Украины В.Л.Рвачев, доцент Е.Б.Коренева,
старший научный сотрудник И.З.Ройтфарб.
Профессор С.Н.Кан привлек автора к развитию приближенных
методов решения задач строительной механики. С исключительным
вниманием отнесся профессор Л.П.Винокуров, поддержавший переориентацию
интересов на проблематику, выходившую за рамки намеченной диссертации.
Большое значение имели контакты с профессорами Б.Г.Кореневым и
П.И.Перлиным. На протяжении длительного периода очень ценными
были советы профессора Г.И.Дринфельда.
Исследования автора поддерживались в местах служебной
деятельности: кафедра строительной механики Харьковского инженерно-строительного
института (ректор – доцент В.П.Сачко, заведующий – профессор А.В.Борисов,
заведующий ОНИЛ А.С.Шевченко, профессора В.А.Воблых, Н.М.Григорьянц,
В.И.Пустынников, доцент Н.В.Зинченко); Северо-Восточный научный
центр НАН Украины (директор – кандидат экономических наук П.Т.Бубенко,
ученый секретарь – доцент В.А.Фрыдынский, заведующий отделом А.Л.Разумовский);
АО “Научно-технологический институт транскрипции, трансляции и
репликации” (президент С.И.Чернышов, вице-президент В.М.Замолоцкий,
директор С.И.Доценко); АО “Межрегиональная электротехническая
ассоциация” (президент – кандидат технических наук А.Л.Лившиц,
генеральный директор – В.Г.Кацман); АО “Украинские информационные
системы” (президент – профессор Э.А.Симсон; председатель правления
В.Б.Любецкая); АО “Концерн АВЭК и Ко” (президент А.Б.Фельдман,
советник президента Г.К.Броншпак, начальник аналитического отдела
С.В.Ингульцов).
Важную роль в развитии представлений о причинно-следственных
связях сыграли практические разработки по междисциплинарной проблематике,
выполнявшиеся во взаимодействии со следующими специалистами: профессора
Н.Н.Внукова, В.М.Московкин, доктор технических наук И.Г.Киуила,
доценты Л.Б.Гержула, А.С.Гугель, Э.А.Молдавский, В.А.Фильштинский,
В.А.Фрыдынский, кандидаты технических наук В.Е.Васильев, С.И.Доценко,
В.М.Замолоцкий, директор экологического центра “Регион” В.В.Ганичев,
заместитель главного инженера ПЭО “Харьковэнерго” С.Т.Прищепов.
Большую поддержку оказали многолетние дружеские
отношения с А.В.Долгаревым, А.И.Коробовым, А.Мангуби, А.Л.Разумовским,
А.С.Шевченко, И.Г.Шепеленко, В.В.Шестаковым и К.З.Ягудиным.
Автор глубоко признателен Б.Д.Шелихову за оформление
рукописи и И.А.Степанову за помощь в части Internet.

