|
|
|
|
|
Пусть 
– симметричное положительно определенное ядро
и уравнение (2.1) разрешимо. Тогда, как показал В.М.Фридман [17], последовательность
функций, определяемых итерациями
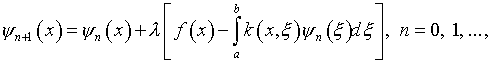(2.10)
сходится в 
к решению уравнения (2.1)
при произвольном выборе начального приближения 
и 
где 
– наименьшее характеристическое число
ядра 
М.А.Красносельский [18] распространил данный результат на любое имеющее
решение уравнение вида (2.1) с линейным ограниченным оператором 
в гильбертовом пространстве 
Доказана теорема о сходимости к решению
последовательных приближений
(2.11)
где 
– тождественный оператор; 
– оператор, сопряженный 
Заметим, что в случае интегрального оператора (2.1)
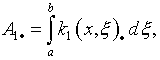
где
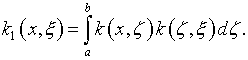
Известен целый ряд процедур убыстрения сходимости итераций по Фридману (см. [10]). Например, при условиях, которые оговорены в отношении процедуры (2.10):
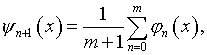(2.12)
где 
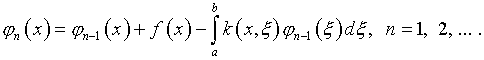
Г.М.Вайникко и А.Ю.Веретенников [19] исследовали итерационный алгоритм неявного типа:
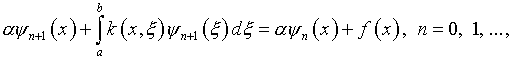(2.13)
где 
параметр 
Следует подчеркнуть, что в отличие от регуляризации вида (2.6), базирующейся
на малости 
для рассматриваемого подхода характерно итерирование
при, напротив, достаточно большом значении указанного параметра. Наряду с этим,
к достоинствам процедур (2.10) – (2.13) относится возможность конструктивного
использования апостериорной оценки погрешности решения для завершения итераций.
В простейшем случае находится номер 
при котором впервые
где 
и 
– погрешности определения соответственно 
и 
– постоянные, удовлетворяющие
ряду требований по обеспечению устойчивости вычислительных операций. Исследовано
также влияние на сходимость последовательных приближений ошибок, малых в вероятностном
смысле.
Авторы [20] привели доводы о целесообразности сочетания регуляризации уравнения вида (2.1), параметром которой является номер итерации, с алгоритмами типа наискорейшего спуска. Такой подход восходит к публикации В.М.Фридмана [21] и реализуется, в частности, по схеме
(2.14)
где
что адекватно выбору шага спуска из условия минимума функционала невязки
