2.4. Обратные задачи
для дифференциальных уравнений математической физики
Современные воззрения по
данной проблематике охарактеризованы в монографии О.М.Алифанова,
Е.А.Артюхина и С.В.Румянцева [20]. В процедуре математической постановки
задач выделены структурная и параметрическая идентификация, подразумевающие
соответственно качественное описание рассматриваемых процессов посредством
дифференциальных операторов и наделение модели количественной информацией.
Содержится также трактовка
физических процессов в категориях причины и следствия. К причинным
показателям отнесены граничные и начальные условия с их параметрами,
коэффициенты дифференциальных уравнений, а также область определения
задачи. Следственные показатели отражают состо-яние исследуемого
объекта, представляя, главным образом, поля различного рода физических
величин.
Восстановление причинных
показателей по информации о физических полях рассматривается в качестве
обратной задачи. К ключевым относится соображение (с.11): “Нарушение
естественной причинно-следственной связи, имеющее место в постановке
обратной задачи, может привести к ее математической некорректности,
чаще всего неустойчивости решения. Поэтому обратные задачи представляют
собой типичный пример некорректно поставленных задач”.
В соответствии с искомой
функцией выделены следующие типы обратных задач идентификации физических
процессов для уравнений в частных производных:
- Ретроспективные – установление
предыстории некоторого состояния процесса.
- Граничные – восстановление
граничных условий или содержащихся в них параметров.
- Коэффициентные – определение
коэффициентов уравнений.
- Геометрические – нахождение
геометрических характеристик контура области или координат точек
внутри нее.
Отмечено принципиальное различие
между обратными задачами идентификации и управления по отношению
к ширине классов возможных решений. Если в первом случае их увеличение
сопряжено с осложнениями при численной реализации, то во втором,
наоборот, является благоприятным фактором. Кстати, алгоритмическое
обеспечение [20] почти всецело базируется на методах решения интегральных
уравнений первого рода, к которым сводятся рассматриваемые задачи
теплообмена.
При постановке обратных задач
математической физики первостепенную значимость имеет доказательство
соответствующих теорем существования и единственности решения. В
этой связи представляет интерес общий подход, схематично обозначенный
А.Л.Бухгеймом [22]. Итак, рассматривается следующая постановка
(2.15)
где Р
– оператор прямой задачи;
Q – “информационный”
оператор, описывающий закон изменения правой части;
g – заданный,
а u и f
– искомые элементы соответствующих
функциональных пространств.
Применение оператора Q
к первому уравнению (2.15) дает QPu=g,
что равносильно
где 
– коммутатор операторов P и
Q.
Смысл коммутирования обуславливается
тем, что, как правило, о функции f
ничего, кроме (2.15), неизвестно и
поэтому оператор Q проще
изучать на решении прямой задачи u,
которое удовлетворяет некоторой совокупности краевых условий. Существенно,
что в типичных приложениях оператор Q
не “портит” часть граничных условий, отражающую область определения
оператора P. В результате
осуществляется своеобразная факторизация обратной задачи (2.15)
в произведение двух прямых задач, порождаемых операторами P
и Q при условии, что
указанный коммутатор им в некотором смысле “подчинен”.
В тривиальном случае 
исходная задача распадается на две более простые: 
.
Для описания свойств используемых операторов привлекаются априорные
оценки.
Представляют интерес выдержки
из введения монографии Р.Латтеса и Ж.-Л.Лионса [23]: “В этой книге
мы предлагаем метод квазиобращения, предназначенный для численного
решения некоторых классов граничных задач, некорректных по Адамару.
Практическая и теоретическая важность таких задач все более осознается
исследователями”. И далее: “Основная идея метода квазиобращения
(универсальная в численном анализе!) заключается в надлежащем изменении
операторов, входящих в задачу. Это изменение производится введением
добавочных дифференциальных членов, которые
а) достаточно “малы” (могут
быть устремлены к нулю);
б) “вырождаются на границе”
(для того, чтобы, например, предупредить возникновение сложных граничных
условий, а также условий, в которые могут войти неизвестные, подлежащие
определению)”.
В частности, некорректная
постановка задачи теплопроводности
(2.16)
где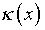 
– известная функция, заменена следующей, с малым параметром 
:
(2.17)
Авторы отмечают (с.36): “При
численной реализации естественно выбирать e
наименее возможным, однако в задачах рассматриваемого типа следует
ожидать численную неустойчивость при 
.
Поэтому можно рассчитывать только на то, что для каждой задачи существует
некоторое оптимальное значение e,
равное e 0”.
На отсутствие сходимости “в обычном смысле” решения задачи (2.17)
к точному при
обратили внимание А.Н.Тихонов и В.Я.Арсенин [1, c.52].
