2.6. Сопоставление
основополагающих концепций А.Н.Тихонова и В.М.Фридмана
Исходное предложение А.Н.Тихонова
(1943 г.), позволившее рассматривать некорректно поставленные задачи
путем априорного сужения класса возможных решений, является своего
рода преломлением общей методологии исследования вопросов существования
и единственности в сферу численного анализа. Кстати, 1935 г. датируется
доказательство А.Н.Тихоновым известной теоремы о единственности
решения обратной задачи теплопроводности в неограниченной n-мерной
области при дополнительном условии вида 
.
Рельефной иллюстрацией этих соображений служит алгоритм поиска квазирешения
(2.7) – (2.9), искусственно подчиняющий данные уравнения (2.1) условиям,
типа фигурирующих в теореме Пикара.
За методом регуляризации
А.Н.Тихонова (1963 г.) – глобальная идея предельного перехода к
точному решению по малому параметру задачи, о чем со всей определенностью
сказано в [1, c.56]:
“Отметим, что регуляризующие операторы, зависящие от параметра,
использовались в математике со времен Ньютона. Так, классическая
задача приближенного вычисления производной 
по приближенным (в метрике С) значениям 
может решаться с помощью оператора
”.
Далее вместо точного значения
функции
подставляется приближенное 
,
где 
.
На основании произведенных выкладок утверждается: “Если брать 
,
где 
при 
,
то 
при
и, следовательно, при 
”.
Следует заметить, что, используя
методологию малого параметра, А.Н.Тихонов получил фундаментальные
результаты в области исследования дифференциальных уравнений с сингулярным
возмущением вида
,
где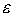 
-
малый параметр; 
– нелинейная функция (1948–1952 гг.)* .
| * См. обзор А.Б.Васильевой [35]. |
Решение приведенной системы
уравнений не зависит непрерывно от параметра .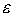
Предельный переход 
порождает объект исследования с совершенно иными свойствами. Подразумевается
в первую очередь проблематика так называемого нарушения устойчивости
корня уравнения 
.
Тем не менее, А.Н.Тихонов сумел построить весьма конструктивную
теорию, на основе которой был развит целый ряд плодотворных направлений
как фундаментального, так и прикладного характера. Значимость отмеченных
достижений А.Н.Тихонова в сфере системного анализа детально проанализировал
Н.Н.Моисеев [36, п.5].
Однако свойства интегрального
уравнения (2.6) при 
также радикально меняются и в этой связи, вообще говоря, возникает
определенная аналогия. Можно предположить, что А.Н.Тихонов предпринял
попытку использовать положения разработанного им аппарата теории
сингулярных возмущений для решения некорректно поставленных задач.
Данное соображение подтверждает
выдержка из монографии С.А.Ломова [37, c.12]:
“В настоящее время становится ясным, как выделять в сингулярно возмущенных
дифференциальных уравнениях малые члены, которыми можно пренебречь.
Оказалось, что для этого необходима дополнительная информация о
решении”.
Известно замечание Ж.Адамара
в смысле того, что к распространению методов теории обыкновенных
дифференциальных уравнений на задачи математической физики следует
подходить с большой осторожностью [38, c.38].
Вместе с тем на рубеже 50-х гг. теория сингулярных возмущений стала
эффективно использоваться при исследовании сложных задач для уравнений
с частными производными (работы М.И.Вишика и Л.А.Люстерника, О.А.Олейник,
К.О.Фридрихса и ряд других). Кстати, поясняя концептуальную основу
своего метода квазиобращения, на перечисленных авторов, а также
А.Н.Тихонова ссылаются Р.Латтес и Ж.-Л.Лионс [23, c.11]*
.
| * Идейную близость квазиобращения и регуляризации
по Тихонову отметил М.М.Лаврентьев [23, c.5]. |
Одновременно они указали,
что приоритетной публикации А.Н.Тихонова по методу регуляризации
[8] (см. также [39]) предшествовала статья Д.Л.Филлипса [40], результаты
которой применительно к интегральным уравнениям аналогичны. В монографии
Ф.Наттерера [41] данная регуляризация фигурирует как метод Тихонова
– Филлипса. Гораздо скромнее оценил достижения последнего В.А.Морозов
[6, c.10]:
“Некоторые рекомендации по использованию этого метода содержатся
в работах Л.В.Канторовича [42] и Д.Л.Филлипса [40]. Теоретического
обоснования этого подхода в указанных работах нет”.
Из хронологической справки
о наиболее существенных результатах в области построения устойчивых
алгоритмов решения интегральных уравнений первого рода [10, c.234]:
“1962 г. – работа Филлипса [40], в которой предложен вариационный
метод условной минимизации функционала (с использованием ограничений
на гладкость решения) и высказана идея способа невязки выбора значения
параметра регуляризации a”.
Обращаясь к достижениям В.М.Фридмана,
заметим, что весьма сложно судить о предпосылках, заложенных в основу
итерационной процедуры (2.10). На первый взгляд, подобного типа
вычислительный прием имеет множество аналогов, однако весьма неожиданной
оказалась его, в определенном смысле, адекватность объекту исследования
– некорректной задаче для интегрального уравнения Фредгольма первого
рода.
В дальнейшем, с целью улучшения
сходимости, В.М.Фридман использовал также нелинейный алгоритм (2.14).
По нашему мнению, различного рода способы определения номера заключительной
итерации и повышения скорости сходимости в целом (см. [14, 19, 20]),
несмотря на их актуальность для практических приложений, следует
трактовать в качестве технического сопровождения методологии В.М.Фридмана.
В настоящее время алгоритмы
сопряженных градиентов считаются едва ли не наиболее эффективными
при решении больших плохо обусловленных разреженных систем линейных
алгебраических уравнений, к которым сводится, пожалуй, большая часть
задач математического моделирования [32, 43, 44]. Как отметил Дж.Ортега
[32], данный метод был предложен М.Р.Хестенсом и Э.Л.Штифелем (1952
г.), однако на протяжении длительного периода в силу ряда обстоятельств
широко не применялся. Интерес к нему резко возрос на рубеже 70-х
гг., когда удалось осознать реальную сферу приложений, потенциал
отмеченного выше предобусловливания и адаптивность к распараллеливанию
вычислительных операций в сочетании с архитектурой современных компьютеров.
Итак, приоритетность метода
сопряженных градиентов обеспечило его преломление на класс задач
линейной алгебры, характеризующихся неустойчивостью численной реализации,
то есть по существу некорректно поставленных. Подчеркнем в этой
связи, что “методы типа наискорейшего спуска” В.М.Фридмана [21]
можно трактовать в качестве несколько упрощенных представителей
семейства методов сопряженных градиентов [20, п.2.1; 43, п.7.1].
Как представляется, В.М.Фридман, первым целенаправленно применивший
итерации для решения некорректно поставленной задачи, в значительной
мере предвосхитил последующее развитие вычислительной математики.
В свете изложенного обращает
внимание позиция М.А.Красносельского и соавторов [18]. О роли В.М.Фридмана
в разработке итерационной процедуры (2.11), являющейся аналогом
(2.10), сказано следующее: “Переход к уравнению 
указывался для некоторых случаев И.П.Натансоном [45]. Для интегральных
уравнений Фредгольма второго рода он применялся еще Г.Виарда [46].
Для интегральных уравнений первого рода он использован по существу
в работе В.М.Фридмана [17]” (с. 73). При этом качественное различие
объектов исследования осталось без комментарий.
Неординарность подхода В.М.Фридмана
подчеркивает, кстати, замечание И.П.Натансона [45]: “Для решения
интегрального уравнения первого рода наш метод неприменим. Это можно
было предвидеть заранее, потому, что в случае применения метода
свободный член в уравнении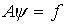 
может быть совершенно произвольным, в то время как уравнение (2.1)
разрешимо не при всех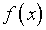 
”.
Далее приведено развернутое обоснование вырожденности соответствующей
дискретной задачи.
Градиентный алгоритм В.М.Фридмана
[21] упомянут авторами [18] исключительно в контексте уравнения
,
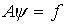у которого оба оператора А
и А-1
ограничены (с.115). Из резюме В.М.Фридмана к статье [21]: “Приведено
новое доказательство сходимости методов типа наискорейшего спуска
для линейного операторного уравнения и при этом не предполагается
как в работах Л.В.Канторовича [47] и М.А.Красносельского, С.Г.Крейна
[48], что нуль есть изолированная точка спектра оператора”*.
| * Последнее адекватно ограниченности оператора
А-1. |
