2.7. Плохо обусловленные
конечномерные задачи и вопросы дискретизации
В настоящем подразделе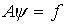 
обозначает систему линейных алгебраических уравнений. Число обусловленности
матрицы А
(см., например, [49])
,
где y
– множество векторов евклидового пространства, представляет повышающий
коэффициент между относительной погрешностью данных и решения. Наряду
с этим 
характеризует меру близости А
к вырожденной матрице, при которой решение соответствующей системы
линейных алгебраических уравнений не существует, или же не является
единственным.
Алгоритм решения вырожденной
системы линейных алгебраических уравнений, базирующийся на методе
наименьших квадратов, изложен в работе А.Н.Малышева [50]. Вначале
матрица А
с помощью специального преобразования приводится к двухдиагональной
и находятся ее собственные значения, которые разбиваются на две
группы: 
так, чтобы 
было не слишком велико. Затем с помощью достаточно трудоемкой процедуры
исчерпывания второй группы собственных значений строится матрица
Аn,
начиная с некоторого значения n,
устойчиво обратимая. Точность получаемого таким образом обобщенного
решения 
определяется по невязке 
с привлечением эвристических соображений.
Как представляется, в плане
методологии данная схема напоминает алгоритм В.К.Иванова [15], который
отражают расчетные соотношения (2.7) -
(2.9).
Л.Хейгеман и Д.Янг [43] исследовали
способ предобусловливания, используемый при решении систем линейных
алгебраических уравнений, близких к вырожденным, для ускорения по
методу сопряженных градиентов итераций вида
,
где 
.
При этом данная процедура предполагается симметризуемой в смысле
существования невырожденной матрицы W,
такой, что матрица 
является симметричной и положительно определенной.
Посредством W
исходную задачу оказывается возможным свести к решению гораздо лучше
обусловленной системы линейных алгебраических уравнений 
,
где
Формально, выбор предобусловливателя
не вызывает затруднений, однако на практике приходится разрешать
противоречие между условиями, которым должна удовлетворять матрица
W: “близость”
к А-1
для сокращения числа итераций; “быстрое” вычисление произведения
вида Wy
[51]. В упомянутой работе И.Е.Капорина проанализированы различные
подходы к построению предобусловливателей для систем линейных алгебраических
уравнений общего вида. Аналогичная проблематика в изложении Дж.Ортега
[32] ориентирована, главным образом, на разреженные матрицы.
Сложность задач линейной
алгебры, возникающих при реализации современных методов исследований
в области механики сплошной среды, охарактеризована следующим образом
[51]: “Матрицы соответствующих систем имеют довольно большой размер
(до сотен тысяч ненулевых элементов), достаточно сильно заполнены
(до сотен и даже тысяч ненулевых элементов в каждой строке), не
имеют диагонального преобладания, не являются М-матрицами
и довольно плохо обусловлены. В общем можно рассчитывать лишь на
симметрию и положительную определенность матрицы системы” *.
| * У М-матрицы внедиагональные элементы неположительны, а
все элементы обратной к ней матрицы неотрицательны. |
Заметим, что, например,
в сейсмической томографии [44] приходится довольствоваться численной
реализацией дискретных аналогов интегральных уравнений первого
рода, поскольку их ядра не представимы аналитически и параметры
рассматриваемых моделей определяются с помощью натурных экспериментов.
В свете изложенного, архаичными
могут показаться соображения Р.В.Хемминга [52, c.360]:
“Говорят, что система линейных уравнений является плохо обусловленной,
если, грубо говоря, уравнения почти линейно зависимы. Много усилий
ушло на изучение того, как решать плохо обусловленные системы. Однако
можно поставить вопрос: требуется ли решать такие системы в практических
ситуациях? В какой физической ситуации окажутся полезными ответы,
когда они так ощутимо зависят от коэффициентов системы? Обычно справедливо
следующее: вместо ответа ищут систему почти линейно независимых
уравнений. В свете этой информации задача может быть лучше понята
и обычно переформулирована снова более удовлетворительным образом.
Вполне вероятно, что плохо обусловленные системы уравнений, если
исключить ошибки округления и измерения, являются действительно
линейно зависимыми и, следовательно, не отражают физической ситуации”.
Обратим внимание, в противовес
разработчикам методов вычислительной математики, которые упоминались
выше, на позициях корректности по Адамару – признанный практик.
Из предисловия [52] Р.С.Гутера: “Имя Р.В.Хемминга – известного американского
ученого, бывшего президента ассоциации по вычислительным машинам,
руководителя математической службы “Bell Telephon
Laboratories” и его
работы в области вычислительной математики и теории информации достаточно
хорошо известны и не нуждаются в особых рекомендациях. … Книга “Численные
методы для научных работников и инженеров” бесспорно является выдающимся
явлением в математической литературе”.
Весьма интересно мнение
Р.В.Хемминга о приоритетности вычислительных процедур [52, c.90]:
“Часто думают, что главные проблемы численного анализа сосредоточены
вокруг интерполяции; но это не так. К ним относятся скорее такие
операции, как интегрирование, дифференцирование, нахождение нулей,
максимизация и т.д. в случаях, когда все, что мы имеем или можем
вычислить – это некоторые узлы функции, причем они обычно известны
не точно, а приближенно, так как бывают испорчены погрешностью округления”.
Итак, задача должна ставиться
корректно в условиях неизбежной погрешности данных, что адекватно
предпочтению алгоритмической эффективности качеству исходной информации.
Упомянутая в выдержке интерполяция подразумевает приближенное представление
последней для проведения операций на ЭВМ посредством конечномерной
аппроксимации.
Однако в вычислительной математике
весьма распространены альтернативные концепции, отражением которых
являются замечания К.И.Бабенко [25]: “Для ряда областей численного
анализа теория приближения является тем фундаментом, на котором
покоится здание численного алгоритма” (с.138). “Вводимая в алгоритм
информация характеризуется прежде всего ее объемом… Все остальные
характеристики, как, например, точность являются производными и
не дают истинного представления о вводе” (с.281).
Здесь информация подразумевается
в смысле колмогоровской теории e -энтропии, отождествляющей
ее с протяженностью задаваемой таблицы или алфавита, словами которого
оперирует алгоритм. Соответственно проблематика численного анализа
трактуется в категориях, образно выражаясь, издержки поиска нужных
слов и стирания таблиц при проведении операций.
Вместе с тем, воззрения Р.В.Хемминга
о взаимосвязи между методом исследования и используемой информацией
активно развиваются представительной группой специалистов во граве
с Дж.Траубом и Г.Васильковским. Авторы [53] отмечают (сс.9, 6):
“В этой книге мы строим общую математическую те-орию оптимального
уменьшения неопределенности. Нас интересуют два основных вопроса:
1) Можно ли уменьшить неопределенность до заданного уровня? 2) Сколько
это будет стоить? Цель теории информационной
сложности – дать единый подход к исследованию оптимальных алгоритмов
и их сложности для задач, в которых используется неполная, неточная
или платная информация, и применить общую теорию к конкретным задачам
из разных областей”.
При этом под сложностью
подразумевается количество арифметических операций, время их реализации,
ресурсы памяти ЭВМ и т.п. Интересно, что трактовка понятия вероятности
[52, 53] коррелирует с красноречивым высказыванием Р.Беллмана и
С.Дрейфуса [54, c.342]:
“К счастью, в некоторых случаях имеется очень простой способ преодоления
этой трудности. Вместо того, чтобы пытаться изучать информацию как
“улыбку чеширского кота”, мы рассмотрим действительный физический
процесс, в котором информация используется для выработки решений
*.
| * Улыбка чеширского кота, по сказке Л.Кэррола "Алиса
в стране чудес", существовала от-дельно от упомянутого
кота. (Прим.ред. [54]). |
Величина информации может
быть тогда измерена через эффективность решений.
Таким образом, полезность
информации зависит от ее применения – это наиболее разумная концепция!”
Следует заметить, что конечно
же и процедура конечномерной аппроксимации задач математической
физики, на которой акцентирует внимание К.И.Бабенко, является очень
важной. В самом деле, получаемая дискретная модель может оказаться
некорректной, а используемые алгоритмы численной ре-ализации расходящимися
даже при решении вполне ординарных задач. Пример неустойчивой разностной
схемы приведен С.К.Годуновым и В.С.Рябеньким [55, п.4.9].
К.И.Бабенко подчеркнул также
отсутствие каких-либо общих методов построения конечномерных аналогов
[25, c.622]:
“… обеспечение только аппроксимации недостаточно” … нужно добиться
еще, чтобы дискретная задача “сохраняла тип исходной непрерывной
задачи”. По его мнению, для достижения указанной цели “необходимо
детальное исследование в каждом конкретном случае; и это наиболее
нетривиальная часть работы”.
