3.2. Взаимосвязь с теоремой об обратном операторе

3.2. Взаимосвязь с теоремой об обратном операторе

Отмеченная следственность третьего условия корректности вытекает из теоремы Банаха об обратном операторе [13], весьма оптимистичный смысл которой состоит в следующем. Если решение уравнения (3.1) с 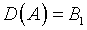и 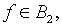где B₁, B₂ – банаховы пространства, существует и единственно, то обратный оператор А^-1 из В₂ в В₁ – ограничен. Соответственно ординарная процедура решения интегрального уравнения Фредгольма первого рода (3.1) по теореме Пикара устойчива при условии, что В₂ совпадает с l₂.

Однако в общем случае как проверка, так и выполнение условия 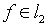– практически неосуществимы, вследствие чего подобные пространства называют “неудобными” (см. [14, 15]). Налицо принципиальная дилемма в выборе методологии исследования:

ориентация на преодоление затруднений, обусловленных исполь-зованием пространства 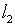, в привязке к ограниченности оператора А^-1;

утрата данного свойства взамен на возможность исследования математических моделей в “удобных” пространствах.

С началом широкомасштабного внедрения в математические исследования вычислительных методов, второе из указанных направлений оказалось доминирующим. Соответственно каноническая формулировка рассматриваемой теоремы С.Банаха, приведенная, например, А.Н.Колмогоровым и С.В.Фоминым [16] (см. п.1.3), стала сопровождаться уточнением о ее правомерности лишь в случае, когда оператор А осуществляет отображение на все пространство В₂ [17, 18]. Следует заметить, что при 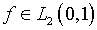данное обстоятельство вполне актуально, поскольку пространство 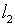, органичное специфике уравнения (3.1), представляет замкнутое подпространство, или же часть .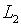

Показательна динамика воззрений С.Г.Михлина, нашедшая отражение в его курсах по математической физике и теории погрешностей 1968, 1977 и 1988 гг. [19–21]. Вначале автор рассматривает уравнение (3.1) в традиционном предположении о том, что оператор А – вполне непрерывен. То есть, по типу отображения внутри пространства 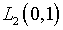. При этом обратный оператор А^-1 – неограничен, вследствие чего стандартные алгоритмы численной реализации неприменимы и следует обращаться к методологии А.Н.Тихонова.

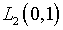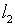В дальнейшем С.Г.Михлин привлек внимание к тому, что если интегральное уравнение Фредгольма первого рода (3.1) трактовать с позиций отображения между пространствами и соответствующий оператор А перестает быть вполне непрерывным, а, следовательно, обратный ему – А^-1 может быть ограниченным и задача восстановления функции становится корректной. При этом, кстати, воссоздается целостность условий корректности, третье из которых автором изначально выделялось.

Итак, использование пары пространств 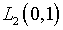– 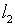как бы переносит каноническую некорректно поставленную задачу в русло фундаментальных основ функционального анализа. Обратим внимание на тот факт, что, являясь математиком, С.Г.Михлин не снизил значимость обозначенного шага расхожими доводами об “удобных – неудобных”, или же “хороших” и “плохих” пространствах.

Такая позиция, вероятно, вызвала критику и в своей заключительной монографии С.Г.Михлин раздраженно переадресует собственно постановку задач математической физики прикладниками, которые заинтересованы в их разрешении, включая социологов. Одновременно автор счел целесообразным не рассматривать бесконечномерные модели с характерными для них аспектами некорректности.

Изречение о том, что, будучи поставлена (подразумевается в рамках предпосылок), математическая задача должна решаться строгими методами принадлежит В.А.Стеклову. Вместе с тем почему бы процедуру постановки задач математической физики не рассматривать в качестве дополнительного резерва повышения эффективности используемого аппарата численной реализации? Более того, не сообщают ли жестко детерминированные формулировки задач искусственные осложнения вычислительного свойства в условиях, когда из физических соображений допустима в некотором смысле малая вариативность? По нашему мнению, постановка задачи математической физики и алгоритм ее численной реализации представляют существенно взаимозависимые категории.

Материал п.1.4 развивает доводы о предпочтительности исследования интегральных уравнений Фредгольма первого рода в паре пространств 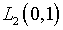– 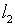. При этом очевидная рассогласованность в общем случае свободного члена 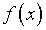с пространством 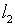позволила наметить конструктивный алгоритм численной реализации посредством адекватного представления возникающей невязки.