3.1. Корректность постановки задач математической физики

3. КРАТКИЕ КОММЕНТАРИИ ПО МАТЕРИАЛАМ ПРИВЕДЕННЫХ РАЗДЕЛОВ И ОБЩИЕ СООБРАЖЕНИЯ

3.1. Корректность постановки задач математической физики

Сформулированные Ж.Адамаром на рубеже начала ХХ столетия условия корректности (см. [1]), которые он затем настойчиво популяризировал, едва ли не в первую очередь поражают неуклонно возрастающей актуальностью затронутой проблематики для практических приложений. Последняя составляет концептуальную основу методов математического моделирования физически содержательных задач, что по существу никем не оспаривается, и вместе с тем на современном этапе возобладали воззрения о принципиальной неправомерности положений Ж.Адамара.

Имеется в виду основополагающее утверждение о том, что из свойств существования и единственности, которые он считал объективно присущими математическим моделям реальных процессов, вытекает корректность постановки адекватных им краевых (начально-краевых) задач, подразумевающая устойчивость используемых алгоритмов численной реализации. При этом, конечно же, далеко не любой в целом вполне жизнеспособный алгоритм способен обеспечить непрерывную зависимость решения от данных конкретной задачи – речь идет о возможности его построения.

Сказанное в первую очередь касается ключевого понятия приведенного утверждения, а именно – корректной постановки задач математической физики. Действительно, со всей определенностью заявлено лишь о ее существовании, из чего, в частности, вытекает, что интегральное уравнение Фредгольма первого рода, попросту говоря, не годится для отражения явлений объективной реальности.

Естественный ход развития исследований, преследующих целью подтвердить, или же опровергнуть гипотезу, а как нам представляется – пророчество Ж.Адамара, казалось, должен был вестись с позиций конструктивной вариативности постановок рассматриваемых задач, однако этого не произошло. Главной причиной, по нашему мнению, явились ошибочные представления в части особой миссии вычислительных средств математического моделирования, легко пренебрегшие даже одним из основных принципов функционального анализа – теоремой Банаха об обратном операторе [2; 3, п.9; 4].

Трудно найти объяснение отсутствию в специальной литературе хотя бы тезиса о необходимости сопряжения постановок задач математической физики с алгоритмами их численной реализации. Корни сложившегося положения видятся в системного характера ориентации гигантского компьютерно-обеспечивающего комплекса на достижение коммерческой эффективности за счет высокой стоимости предоставляемых услуг.

В итоге критика воззрений Ж.Адамара выстраивается альтернативной школой А.Н.Тихонова по схеме:

решение интегрального уравнения Фредгольма первого рода

(3.1)

в общем случае является некорректной задачей (что неоспоримо);

интегральные уравнения этого типа адекватны множеству реальных явлений, в подтверждение чего фактически предъявляется вполне прозрачная интерпретация соответствующих прямых задач (вычисление f по данным k и y ).

Однако на каком основании постановка задачи, обратной вычислению 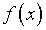, может производиться посредством тривиального переименования в (3.1) заданной и искомой функций? Из того, что при данных 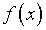и 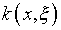процедура восстановления является некорректной, ровным счетом ничего большее не следует.

Интегральное уравнение Фредгольма первого рода – несомненно весьма наглядный объект для иллюстрации предлагаемых соображений. Что касается задач математической физики для уравнений с частными производными, то оценка их не столь однозначна. Так, пример Адамара (1.3), (1.4), связанный с восстановлением функции по начальным условиям, трактуется в качестве прямой задачи, тогда как обратная – напротив, касалась бы определения правых частей по соответствующей информации о решении. При этом постановка прямой задачи – некорректна.

Принято считать, что задача (1.3), (1.4) имеет физические приложения, впрочем, достаточно специальные (см. например, [2]). В таком случае, если следовать методологии Ж.Адамара, ее постановка может быть приведена к корректной. Заметим, что как будет показано ниже, различие между интегральными уравнениями первого рода и краевыми (начально-краевыми) задачами математической физики в некотором смысле условно. В самом деле, задача (1.3), (1.4) вполне элементарно сводится к уравнению указанного типа относительно или .

Упреки в адрес Ж.Адамара, характерные моменты которых воспроизведены в п.1.1, интегративно выражают позицию: великий ученый затормозил развитие науки, не признав адекватность некорректно поставленных задач множеству реальных процессов (см. [3–5]). Однако в том, что последние существуют, Ж.Адамар нисколько не сомневался – фактически он выдвинул тезис о неадекватности используемых средств математического моделирования. Действительно, правомерно ли ставить вопрос о чьей-либо монополии на математическую модель в ракурсе ее объективного соответствия реалиям, которые мы так или иначе наблюдаем?

Понятно, что ответ может быть только отрицательным: математические модели выстраиваются с различной степенью детализации, имеют вид интегральных уравнений, краевых задач и т.д., порождая, кстати, далеко не тождественные осложнения вычислительного характера. Вместе с тем результаты достоверных вариантов математического моделирования конкретных процессов должны являться в целом идентичными.

Могут возникнуть соображения в плане того, что переход от некорректной к корректной постановке задачи – шаг кардинальный, а соответственно должен сопровождаться существенной деформацией расчетных соотношений, которая аналогичным образом повлияет на решение. В пользу такого вывода свидетельствует, казалось бы, и известное положение функционального анализа об устойчивости свойства некорректной разрешимости к малым возмущениям [6]. Однако последнее привязано к паре пространств и, вообще говоря, утрачивает силу при рассмотрении уравнения (3.1) с позиций отображения между пространствам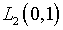и и 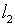, о чем было сказано выше.

Как представляется, обозначен важнейший момент, в развитие которого констатируем отсутствие весомых доводов на предмет невозможности корректно поставить задачу, например, о восстановлении функции по ядру 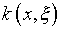и правой части 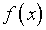, полученной интегрированием по формуле (3.1). Сугубо эвристически, почему не предположить, что если малые вариации данных способны существенно влиять на решение некорректно поставленной задачи, то для преодоления этого эффекта может оказаться достаточной весьма незначительная корректировка традиционной математической модели?

Среди приверженцев исследования задач математической физики исключительно в корректной постановке такие имена как А.Пуанкаре, Д.Гильберт, В.А.Стеклов, И.Г.Петровский, И.Пригожин [7–11]. Наряду с этим едва ли позитивную роль сыграло введение Д.Гильбертом и Р.Курантом [12] трех совершенно независимых условий корректности: существование, единственность и непрерывная зависимость решения от данных задачи. По нашему мнению, конструктивный потенциал того обстоятельства, что третье из них является следствием предыдущих способствовал бы активизации исследований различных аспектов корректной постановки задач математической физики в естественных для них классах функций.

Рассматривая интегральное уравнение Фредгольма первого рода (3.1), пришлось бы внимательнее отнестись к операциям с функцией 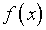из 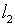в противовес, образно выражаясь, суррогату непрерывной обратимости при условии ее принадлежности . 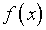Соответственно анализ предпосылок корректной разрешимости указанного уравнения мог бы привести к заключению о том, что задача восстановления на его основе функции по данным и 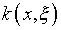не может трактоваться в качестве обратной вычислению 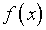по формуле (3.1).