4. МЕТОД СВЕДЕНИЯ ЗАДАЧ, ТРАДИЦИОННО
АССОЦИИРУЕМЫХ С ИНТЕГРАЛЬНЫМИ УРАВНЕНИЯМИ ФРЕДГОЛЬМА ПЕРВОГО РОДА,
К РЕШЕНИЮ
ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ ФРЕДГОЛЬМА ВТОРОГО РОДА
4.1. Структура представления погрешности
В свете соображений п.3.5, продолжим рассмотрение
все того же интегрального уравнения Фредгольма первого рода
 (4.1)
(4.1)
с замкнутым ядром 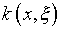 ,
при определении правой части которого одним из способов, включая
интегрирование изначально заданной функции
,
при определении правой части которого одним из способов, включая
интегрирование изначально заданной функции  ,
допущена погрешность
,
допущена погрешность  ,
где
,
где 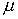 – постоянная. Иначе говоря, свойство корректности присуще уравнению
– постоянная. Иначе говоря, свойство корректности присуще уравнению
 (4.2)
(4.2)
в естественном для него пространстве 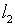 .
.
Следуя (3.5), представим погрешность разностью
искомой функции и интегральной компоненты
 ,
(4.3)
,
(4.3)
где 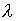 – постоянная, полагая *
– постоянная, полагая *
| * Об использовании в (4.4) неопределенного интеграла будет
сказано ниже. |
 .
(4.4)
.
(4.4)
Подстановка 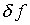 из (4.3) в (4.2) приводит к уравнению
из (4.3) в (4.2) приводит к уравнению
 (4.5)
(4.5)
с двумя неизвестными функциями:  на
на 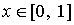 и
и 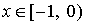 .
Вторым для построения системы могло бы служить уравнение (4.3),
однако в отношении функции
.
Вторым для построения системы могло бы служить уравнение (4.3),
однако в отношении функции  необходима конкретизация.
необходима конкретизация.
Если подразумевается исключительно потеря информации,
обусловленная вычислением 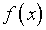 с помощью процедуры интегрирования (4.1), логично полагать, что
с помощью процедуры интегрирования (4.1), логично полагать, что
 (4.6)
(4.6)
или же
 .
(4.7)
.
(4.7)
При этом моделирование погрешности осуществляется
вследствие взаимной неадекватности компонентов правой части (4.3)
качественного характера (в первую очередь, по гладкости). Следует
также принять во внимание, что за исключением тривиального случая
 – постановка (4.1) лишена математического смысла и задача может
рассматриваться лишь с позиций поиска приближенного решения:
– постановка (4.1) лишена математического смысла и задача может
рассматриваться лишь с позиций поиска приближенного решения:
 .
(4.8)
.
(4.8)
С учетом (4.6) уравнение (4.3) представим в виде
 (4.9)
(4.9)
или
 (4.10)
(4.10)
где
 (4.11)
(4.11)
Производя в (4.10) замену переменных:  ,
получаем
,
получаем
 (4.12)
(4.12)
Очевидно, что удовлетворение (4.9) посредством  на
на 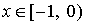 эквивалентно разрешимости уравнения (4.12). Пусть ядро
эквивалентно разрешимости уравнения (4.12). Пусть ядро  замкнуто и
замкнуто и  **.
**.
| ** При этом на основании (4.11) , что,
вообще говоря, изначально подразумевается. |
Тогда (4.12) является интегральным уравнением Фредгольма
первого рода, решение которого в случае его существования – единственно
(см. [1]). Для упрощения последующих выкладок указанное ядро целесообразно
принять симметричным, зависящим от разности аргументов, а также
удовлетворяющим на  условию периодичности. Например,
условию периодичности. Например,
 (4.13)
(4.13)
В этом случае (4.12) приобретает вид интеграла Пуассона
[2]. Соответственно в (4.4)
 .
(4.14)
.
(4.14)
По теореме Пикара необходимым условием сходимости
к решению уравнения (4.12) в  ряда
ряда
 (4.15)
(4.15)
является
 .
(4.16)
.
(4.16)
Здесь характеристические числа и собственные функции
ядра (4.13) имеют вид соответственно [1]:

Однако вследствие (4.11) свободный член  ,
а, следовательно, и коэффициенты
,
а, следовательно, и коэффициенты  зависят от искомой функции
зависят от искомой функции  ,
из-за чего проверить выполнение условия (4.16) – не представляется
возможным. С этой точки зрения весьма актуально замечание Э.Гурса
к теореме Пикара [3, c.142–143],
,
из-за чего проверить выполнение условия (4.16) – не представляется
возможным. С этой точки зрения весьма актуально замечание Э.Гурса
к теореме Пикара [3, c.142–143],
состоящее в следующем.
Ядро  предполагается замкнутым и вместе с тем функция
предполагается замкнутым и вместе с тем функция  такой, что условие (4.16) не выполняется. Тем не менее существует
функция
такой, что условие (4.16) не выполняется. Тем не менее существует
функция  ,
представимая сходящимся рядом (4.15), при подстановке которой интегральное
уравнение Фредгольма первого рода (4.12) удовлетворяется в
,
представимая сходящимся рядом (4.15), при подстановке которой интегральное
уравнение Фредгольма первого рода (4.12) удовлетворяется в  .
.
Доказательство базируется на совпадении
 (4.17)
(4.17)
где
 ,
(4.18)
,
(4.18)
с суммой n первых членов ряда Фурье функции
 по элементам
по элементам 
Следует учесть, что по теореме Мерсера [4]
 .
(4.19)
.
(4.19)
Исходя из этого, n можно выбрать таким, что
интеграл
 (4.20)
(4.20)
не превзойдет сколь угодно малую величину 
Как представляется, данный результат может рассматриваться
в качестве своеобразного дополнения теоремы Рисса-Фишера с предшествующей
ей леммой Вейля [4]. Согласно классификации [5], ряд (4.18) посредством
(4.17) сходится к решению уравнения (4.12) в смысле обобщенной функции
– распределения.
Если условие (4.16) не выполняется, то в 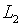 ряд (4.15) – расходящийся ***.
ряд (4.15) – расходящийся ***.
*** Что совсем не эквивалентно заключению:  |
В этой связи интересно установить ограничения на
данные (4.1) для удовлетворения (4.16). Вначале следует симметрировать
уравнение (4.1) путем умножения
на сопряженный оператор
 .
.
Получаем
 .
(4.21)
.
(4.21)
Здесь

и соответственно  .
.
Предположим функция  такова, что решение интегрального уравнения Фредгольма первого рода
(4.21) является задачей, корректно поставленной в пространстве
такова, что решение интегрального уравнения Фредгольма первого рода
(4.21) является задачей, корректно поставленной в пространстве 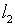 .
Тогда
.
Тогда
 ,
(4.22)
,
(4.22)
где  и
и  - характеристические числа и собственные функции ядра
- характеристические числа и собственные функции ядра  .
.
В этом случае по теореме Пикара решение уравнения
(4.21) определяется рядом
 ,
(4.23)
,
(4.23)
сходящимся в 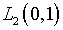 .
Соответственно в (4.12)
.
Соответственно в (4.12)

и с учетом (4.19)

 .
(4.24)
.
(4.24)
Таким образом, использование дополнительного соотношения
(4.9) предполагает, что удовлетворяется не только условие (4.22),
но и (4.16) с коэффициентами (4.24).
Однако в рамках постановки (4.8) правильнее исходить
из того, что сформулированные требования принципиально невыполнимы.
Соответственно ряд (4.18) оказывается при  расходящимся.
расходящимся.
Вместе с тем если значение n является пусть
и достаточно большим, но все же конечным – ситуация диаметрально
меняется. Действительно, условия разрешимости интегральных уравнений
Фредгольма первого рода (4.1) и (4.21) удовлетворяются автоматически;
ряд (4.18) не только сходится в смысле (4.20), но и представляет
собой 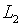 -функцию.
-функцию.
Подчеркнем, это всего лишь наводящие соображения,
на основании которых не представляется возможным утверждать о том,
что  .
Но для последующих выкладок данное условие является необходимым
и поэтому ниже мы обратимся к моделированию погрешности с несколько
иных позиций.
.
Но для последующих выкладок данное условие является необходимым
и поэтому ниже мы обратимся к моделированию погрешности с несколько
иных позиций.
В варианте экспериментального определения, правая
часть уравнения (4.1), как правило, отличается от выражения  ,
получаемого в результате гипотетически точного интегрирования данной
функции
,
получаемого в результате гипотетически точного интегрирования данной
функции  ,
на некоторую величину
,
на некоторую величину  При этом остается только потребовать ее ограниченности, поскольку
в противном случае с одной стороны нарушается адекватность собственно
математической модели, с другой – последующее сведение к интегральному
уравнению Фредгольма второго рода утрачивает практический смысл.
При этом остается только потребовать ее ограниченности, поскольку
в противном случае с одной стороны нарушается адекватность собственно
математической модели, с другой – последующее сведение к интегральному
уравнению Фредгольма второго рода утрачивает практический смысл.
В целом же, по сравнению с 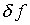 ,
погрешность
,
погрешность  – непринципиальна. Действительно, если
– непринципиальна. Действительно, если

в условиях построения устойчивого алгоритма численной
реализации погрешность искомого решения  окажется сравнительно небольшой. При невыполнении этого требования
как постановка конкретно рассматриваемой задачи, так и ее решение
будут попросту искажены.
окажется сравнительно небольшой. При невыполнении этого требования
как постановка конкретно рассматриваемой задачи, так и ее решение
будут попросту искажены.
Если в (4.4) принять
 (4.25)
(4.25)
то на оговоренном моделировании погрешности данное
обстоятельство отразится всего лишь видоизменением выражения (4.11):

Может рассматриваться также следующий способ представления
погрешности:
 (4.26)
(4.26)
где 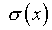 – еще одна неизвестная функция; оператор
– еще одна неизвестная функция; оператор

Очевидно, что  поскольку в противном случае условие (4.6) при
поскольку в противном случае условие (4.6) при 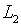 -ядре
-ядре
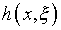 сводится к однородному интегральному уравнению Вольтерра второго
рода
сводится к однородному интегральному уравнению Вольтерра второго
рода

решение которого тривиально.

