4.3. Конструктивный алгоритм практической реализации
Обращая оператор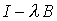 
в (4.27), (4.29), получаем соответственно
(4.35)
(4.36)
и
(4.37)
где
(4.38)
Из уравнения (4.30)
В результате подстановки выражений (4.31) и (4.36)
с учетом (4.35), а также функционального соотношения [7]
(4.39)
получаем
.
(4.40)
Основой для построения системы, то есть – в дополнение
(4.37) еще одного интегрального уравнения Фредгольма второго рода
будет служить (4.28):
(4.41)
При этом очевидно, что входящую явно функцию 
нельзя представить с помощью (4.36), так как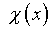 
в левой части сократится *.
| * Таким образом, мы тривиально возвратились бы к исходному
объекту (4.1). |
Поэтому воспользуемся решением уравнения (4.30)
(4.42)
С учетом (4.40), (4.39), свойства ортогональности
(4.43)
обусловленного тем, что ядро (4.14) обладает периодичностью
не только на 
,
но также и 
,
а, кроме того, вследствие (4.19), (4.34)
,
находим
.
(4.44)
Для определения других компонентов правой части
(4.41) выражение (4.36) вполне подходит. Подстановка (4.35), (4.36)
и (4.44) в (4.41) с учетом (4.39) приводит к уравнению
.
(4.45)
Заметим, что на основании (4.34) в (4.38) и (4.45)
;
,
где
Вследствие симметрии и периодичности 
,
оператор
допускает обращение в аналитическом виде (аналогично
изложенному выше, можно построить соответствующую резольвенту).
Вместе с тем реализация данной процедуры не способствовала бы заметному
упрощению уравнения (4.45).
Обращение в (4.37) оператора
при 
,
где 
– его характеристические числа, приводит к выражению
(4.46)
Здесь 
– резольвента ядра (4.38).
Практически, для ее построения решение можно представить
рядом
,
где 
– постоянные, определяемые из системы линейных алгебраических уравнений,
которая получается приведением множителей элементов 
.
В этой связи отметим также разработанный С.Г.Михлиным метод численной
реализации резольвенты [8, п.12].
Подстановка выражения (4.46) в (4.45) позволяет
свести рассматрива-емую задачу к решению интегрального уравнения
Фредгольма второго рода относительно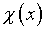 
.
Конкретно, в интересах придания системе интегральных
уравнений Фредгольма второго рода (4.37) и (4.45) канонического
вида примем
(4.47)
Используем также обозначения:
;
(4.48)
;
(4.49)
С учетом (4.43), а также очевидного свойства
уравнения (4.45), (4.37) приобретают вид соответственно
(4.50)
Как показано в [4, c.195–196], данная система эквивалентна
интегральному уравнению Фредгольма второго рода
,
(4.51)
где
(4.52)
(4.53)
(4.54)
В случае
(4.55)
решение уравнения (4.51) достигается путем последовательных
приближений [9]
(4.56)
при произвольном выборе 
**.
| ** Так называемый метод простых итераций. |
Если наряду с (4.55)
(4.57)
- эта сходимость регулярная. Естественно, параметр
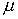не должен совпадать с характеристическими числами ядра (4.54).
Следует принять во внимание, что процедура (4.56)
по существу эквивалентна построению резольвенты [7]
,
где
- итерированные ядра 
.
Итерации вида (4.56) при условиях (4.55), (4.57)
могут быть применены к системе интегральных уравнений Фредгольма
второго рода (4.50) непосредственно. При этом для определения необходимого
значения 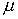подходят
также средства вычислительного эксперимента. Отождествление (4.47)
несколько сужает его вариативность.
Заметим, что для решения интегральных уравнений
Фредгольма второго рода, включая определение спектральных характеристик
и вычисление квадратур, имеется целый ряд эффективных алгоритмов
(библиография по данной проблематике практически неисчерпаема [10–13]).
Положения общей теории приближенных методов численной реализации
уравнений указанного типа наиболее обстоятельно изложены в [14].
Следует подчеркнуть, что структура ядра
не навязывает ему каких-либо дополнительных особенностей или осцилляций,
выходящих за рамки исходной постановки (4.1) ***.
| *** Иначе говоря, порождаемых внутренними проблемами используемого
метода. |
Зная 
,
по формуле (4.36) находим
(4.58)
Функция 
представляет собой решение рассматриваемой задачи (4.1) в смысле
(4.8). То есть, именно при 
достигается
,
где
.
По существу, мы определяем таким образом максимально
возможное в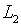 
приближение результата интегрирования (4.1), объективно принадлежащего
пространству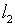 
,
к свободному члену 
,
содержащему те или иные погрешности (измерений, аппроксимаций и
т.п.). Соответственно в развитие (4.8) решение задачи (4.1) приобретает
смысл
.
(4.59)
Как представляется, данный момент принципиально
важен.
