4.4. Вопросы обоснования и механизм достигаемой
результативности
Из (4.50) с учетом (4.1) и (4.49) вытекает, что
удовлетворяющая (4.51) функция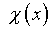 
является также решением системы однородных интегральных уравнений
Фредгольма второго рода
(4.60)
где
.
Но если не принимать во внимание тонкости, связанные
с характером зависимости ядер 
и 
от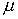 
,
при значении данного параметра, не совпадающем с характеристическими
числами однородного уравнения
,
в котором ядро 
определяется согласно (4.54), (4.49) с заменой 
на 
,
решение (4.60) – тривиально. Итак, видится противоречие.
Обратимся к уравнению (4.27):
,
(4.61)
предполагая, что функция 
в явном виде определена посредством (4.36), тогда как остальные
компоненты – аналогично (4.41). В результате вычитания из последнего
уравнения – (4.61) с учетом (4.36) и (4.44)
.
(4.62)
Здесь
,
(4.63)
где 
– решение задачи (4.1), вычисленное как указано в п.4.3.
Подстановка выражения (4.46) в (4.62) с учетом (4.43)
и (4.47) приводит к интегральному уравнению Фредгольма второго рода
.
(4.64)
Здесь
где 
– резольвента ядра (4.38).
Предположим, что погрешность в определении свободного
члена (4.1) отсутствует. Иначе говоря, мы находимся в ситуации 
.
Тогда алгоритм п.4.3 должен привести к 
и вследствие (4.63) уравнение (4.64) становится однородным.
В смысловом отношении данное обстоятельство вполне
закономерно, поскольку интерпретирует тождественность различных
представлений, а именно – (4.36) и (4.44), функции
на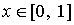 
.
Но с формальных позиций, решение однородного уравнения
(4.65)
– тривиально, или же при 
,
где 
- характеристические числа ядра 
,
совпадает с его собственными функциями.
Следует однако заметить, что, используя предпосылку
о точном удовлетворении (4.1), мы не можем рассматривать уравнение
(4.65) абстрактно – его решение необходимо искать в более узком
классе функций, адекватном сходящемуся ряду (4.23). Подстановка
последнего в (4.65) при гипотетически точной реализации соответствующих
преобразований должна привести к тождеству. Сокращение параметра
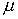логично представить в контексте соотношения (4.39).
В общем случае приближенного определения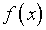 
,
уравнения (4.28) и (4.29) дополняются погрешностью 
,
о чем упоминалось выше. Поэтому на основании сказанного в отношении
(4.2), к свободному члену уравнения (4.28) прибавим и из него же
вычтем 
.
С учетом данного обстоятельства в (4.37), (4.40) и (4.42) появятся
корректирующие компоненты. Используя технику преобразований п.4.3,
а также соотношение [7]
,
получаем соответственно
,
где
.
Одновременно в (4.63) появляется слагаемое
и с учетом определения (4.2) вместо (4.65) получаем
.
(4.66)
Если использовать обозначение
,
и, кроме того, представить
(то есть, возникающая поправка достигается за счет
вариации связующей функции 
),
уравнение (4.66) приобретает вид
.
В этой связи алгоритм п.4.3 можно интерпретировать
следующим образом. Имеется функция
,
позволяющая посредством (4.58) удовлетворить уравнению (4.1) точно,
или же с некоторой погрешностью. Вполне очевидно также существование
однородного интегрального уравнения Фредгольма второго рода с собственной
функцией .
Приведенные соображения позволяют сделать вывод о том, что в качестве
такого уравнения выступает (4.65).
Естественно, с точностью, зависящей от погрешности
определения свободного члена (4.1) *.
* Его несоответствия пространству  . |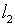
При этом адаптивная привязка к значению параметра
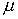осуществляется посредством вариации 
,
эквивалентной смещению спектральных характеристик. В свете изложенного,
обозначенное выше противоречие можно считать исчерпанным.
Понятно, что, как правило, погрешность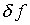 
,
а соответственно и корректирующая компонента
в (4.66) – неизвестны и фактически мы имеем интегральное уравнение
Фредгольма второго рода
.
(4.67)
Найденная из него функция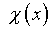
позволяет по формуле (4.36) вычислить решение рассматриваемой задачи
в смысле (4.59).
Заметим, что структура уравнения (4.65) обусловлена
дифференциацией представления
на :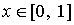
с функцией
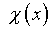в явном виде – (4.36) и посредством ее интегрирования – (4.44).
По существу, это ключевое звено алгоритма. Возможность его реализации
обеспечила, в первую очередь, трансформация постановки (4.1), а
точнее равенство нулю свободного члена (4.27) на части интервала
определения. Последнее вытекает из модели представления погрешности
(4.3) – основополагающей концепции настоящего исследования.
Итак, задача (4.1) сводится к решению интегрального
уравнения Фредгольма первого рода (4.51) (системы аналогичных уравнений
– (4.50)), компоненты которых определяются согласно (4.52) – (4.54)
и (4.49), а также (4.14), (4.19) и (4.34) при условиях в отношении
параметра :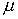
(4.47) и отличие от характеристических чисел ядра (4.54). Для упрощения
процедуры численной реализации его целесообразно принять удовлетворяющим
(4.55), а возможно и (4.57). При использовании уравнения (4.67)
значение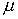
не должно совпадать с характеристическими числами ядра (4.38).
Констатируем, что наши соображения о целесообразности
представления погрешности в виде (4.3) с использованием вместо (4.1)
трансформированной постановки (4.27), (4.28) и (4.30) оправдались.
Стоит подчеркнуть, до практического сведения рассматриваемой задачи
к решению интегральных уравнений Фредгольма второго рода – изложенные
выше доводы о перспективности предлагаемого подхода являлись эвристическими.
С предметной точки зрения, главным является моделирование
погрешности вычисления функции 
по формуле (4.1) разностью между искомой функцией
в явном виде и интегралом от нее – (4.4). Иначе говоря, качественно
адекватная интерпретация механизма сглаживания информации.
Представление оператора В интегралом Пуассона,
конечно же, не единственно приемлемое. Вместе с тем данный момент
не принципиален, вследствие чего выражение ядра (4.14) можно считать
универсальным. Если значимость упомянутой структуры представления
(4.3) естественно охарактеризовать в плане идейно-методологическом,
то оператор В с ядром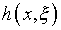 
способствует выполнению конструктивно-технических функций, что также
необходимо для реализации алгоритма.
При построении интегрального уравнения Фредгольма
второго рода (4.51) какая-либо дополнительная информация о данных
задачи (4.1), за исключением принадлежности пространству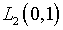 
,
не привлекалась и, следовательно, его логично рассматривать в качестве
объективного эквивалента постановке, которая ошибочно считается
безальтернативно некорректной. Что касается погрешности в определении
,
а также 
,
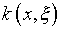то их влияние на решение (4.51), как и реальных задач, которые принято
отождествлять с постановкой (4.1), переводится в плоскость устойчивых
зависимостей теории операторных уравнений второго рода [14].
