5. РЕДУКЦИЯ ЛИНЕЙНЫХ КРАЕВЫХ И
НАЧАЛЬНО-КРАЕВЫХ ЗАДАЧ К ИНТЕГРАЛЬНЫМ УРАВНЕНИЯМ ФРЕДГОЛЬМА ПЕРВОГО
РОДА
5.1. Задачи для обыкновенных дифференциальных
уравнений
Пусть, например,
(5.1)
(5.2)
где 
и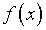 
– данные 
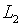-функции.
Из обозначения
(5.3)
вытекает
;
(5.4)
(5.5)
где 
,
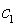– постоянные интегрирования.
Подстановка выражений (5.3) и (5.5) в (5.1) приводит
в интегральному уравнению Вольтерра второго рода относительно новой
неизвестной функции:
(5.6)
решение которого имеет вид
(5.7)
где 
– резольвента ядра 
Из граничных условий (5.2) с учетом (5.4), (5.5)
и (5.7) находим 
;
(5.8)
Можно поступить иначе, а именно, подставив выражения
(5.4), (5.5) в (5.2), получить 
;
в результате чего
(5.9)
и рассматриваемая задача сводится к интегральному
уравнению Фредгольма второго рода
(5.10)
Его решение
(5.11)
где
– резольвента ядра
при параметре 
в правой части (5.10) *.
| * Понятно, что она нетождественна резольвенте уравнения (5.6). |
Подстановка выражения (5.7) с учетом (5.8) в (5.5),
или же (5.11) в (5.9) позволяет вычислить решение задачи (5.1),
(5.2).
Заметим, что намеченный подход в значительной мере
индифферентен к порядку дифференциального уравнения, виду начальных
или граничных условий, а также данным конкретно рассматриваемой
задачи, таким как функции 
и 
.
При сведении задач к интегральным уравнениям типа Фредгольма в общем
случае требуется исследование их разрешимости. Иначе говоря, проверка
принадлежности
совокупности характеристических чисел соответствующего однородного
уравнения, которая осуществляется на основании положений общей теории.
Аналогичные преобразования традиционно освещаются
в курсах по теории интегральных уравнений (см., например, [1, 2].
Вместе с тем при решении прикладных задач, что можно охарактеризовать
как своеобразный парадокс, методология сведения к интегральным уравнениям
второго рода не получила широкого распространения. И это несмотря
на весьма активные попытки ее популяризации, из которых можно выделить
публикации Ш.Е.Микеладзе, И.А.Биргера, А.Н.Голубенцева [3–5].
По нашему мнению, причиной такого положения явились
с одной стороны сугубо технические осложнения при численной реализации
интегральных уравнений до широкого внедрения ЭВМ; с другой – системная
ориентация на использование аппарата фундаментальных решений, которая
сформировалась под воздействием общеметодологических концепций исследования
задач математической физики. Действительно, интегральные уравнения,
как правило, строились на основе идей теории потенциала, когда в
качестве ядра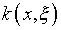 
выступало решение от сосредоточенного источника, а искомой функцией
являлось распределение интенсивности соответствующего воздействия.
В этом контексте весьма интересно развитие воззрений
о взаимосвязи между понятиями производной, неопределенного и определенного
интегралов, детально прослеженное Ф.А.Медведевым [6]. По существу,
будучи изначально обратимыми, под влиянием усложнения структур используемых
ядер они ди-аметрально разошлись, превратившись в практически самостоятельные.
Отметим также, что представление решений посредством различного
рода локальных воздействий оказалось созвучным с инженерными приемами
в целом ряде дисциплин, которые широко применялись до появления
технических средств эффективной реализации вычислительных операций.
В целом, положение о возможности сравнительно элементарного
сведения относительно старшей производной краевых задач для обыкновенных
дифференциальных уравнений к интегральным уравнениям Вольтерра или
Фредгольма второго рода не нашло в сферах приложений адекватного
восприятия.
