5.2. Иллюстрация используемой процедуры сведения
Обратимся к модели изгиба равномерной нагрузкой
растянутой по контуру мембраны, или же – кручения бруса:
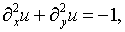(5.12)
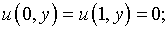(5.13)
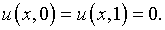(5.14)
Из обозначения
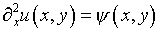(5.15)
вытекает
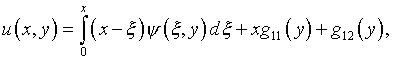(5.16)
где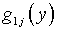 
– функции интегрирования.
С учетом (5.15) уравнение (5.12) приобретает вид
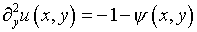
и соответственно
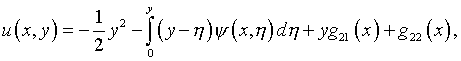(5.17)
где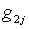 
– также функции интегрирования.
Подстановка выражений (5.16), (5.17), в граничные
условия соответственно (5.13) и (5.14) позволяет определить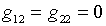 
;
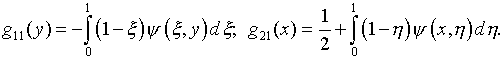
В результате
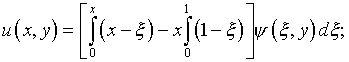(5.18)
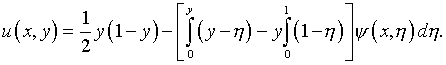(5.19)
Исключая из этих выражений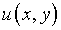 
,
получаем интегральное уравнение Фредгольма первого рода относительно
новой неизвестной функции:
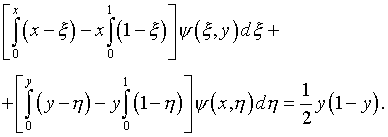(5.20)
Итак, принципиальное отличие от одномерного случая
состоит в сведении рассматриваемой задачи (5.12) – (5.14) к поставленной
некорректно. Однако в настоящем нас будет интересовать не численная
реализация уравнения (5.20) (заметим лишь, что алгоритм предыдущего
раздела на него распространяется), а собственно универсальность
процедуры преобразований.
В самом деле, пусть область определения задачи отлична
от канонической и, например, второе условие (5.13) имеет вид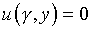 
,
где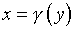 
– некоторая однозначная функция. При этом вместо (5.18)
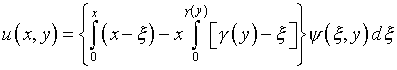
и какие-либо существенные изменения отсутствуют,
поскольку для перехода к ординарной операции вычисления интеграла
достаточно всего лишь воспользоваться неортогональным отображением
вида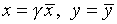 
.
Нетрудно заметить, что каждое из выражений (5.18),
(5.19) тождественно удовлетворяет паре граничных условий, соответственно
(5.13) и (5.14). Остальные выполняются приближенно – в зависимости
от точности вычисления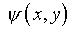 
.
Вместе с тем решение можно представить в виде, тождественно удовлетворяющем
как условиям (5.13), так и (5.14):
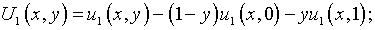
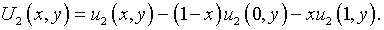
Здесь функции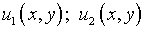 
определяются по формулам соответственно (5.18) и (5.19).
Норма невязки значени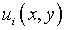й 
или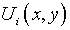 
позволяет оценивать погрешность приближенного решения:
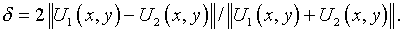
Однако, если вместо (5.13) были бы поставлены условия
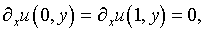
вытекающее из (5.15) выражение производной
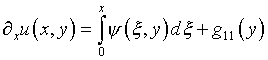
для их удовлетворения не подходит.
Тем не менее данное осложнение легко преодолевается
путем использования, в частности, соотношения
,
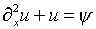позволяющего сохранить присутствие обоих функций
интегрирования .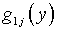
В общем случае целесообразно обратиться к эквивалентной
формулировке задачи (5.12) – (5.14):
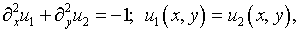(5.21)
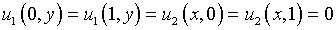(5.22)
с использованием представлений решения вида
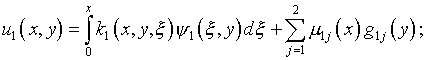
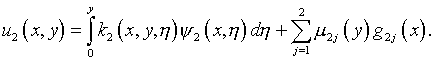
Предполагается, что ядра, удовлетворяющие условиям
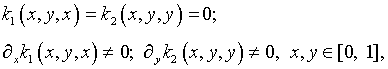(5.23)
– заданы;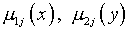 
– также заданные функции; 
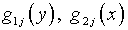– подлежат определению из граничных условий аналогично изложенному
выше.
Так, в соответствие с предыдущей схемой можно принять
.
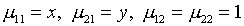При этом из условий (5.22) следуют выражения
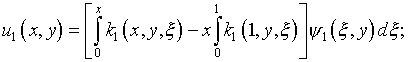(5.24)
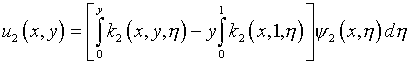(5.25)
и соответственно
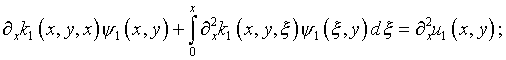(5.26)
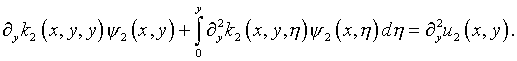(5.27)
Пусть в дополнение условий (5.23)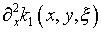 
и 
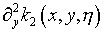являются L2-ядрами. С учетом априорной информации
о решении рассматриваемой задачи, (5.26), (5.27) представляют собой
интегральные уравнения Вольтерра второго рода относительно функций
,
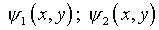решения которых в соответствии с положениями общей теории существуют
и единственны. Следовательно, выражения (5.24) и (5.25) адекватны
физическому содержанию задачи (5.21), (5.22).
Заметим, что при отличном от указанного выборе
элементов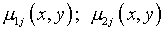 
построенные таким же образом интегральные уравнения могли бы принадлежать
типу Фредгольма второго рода. В этом случае ядра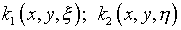 
должны удовлетворять еще и условию их разрешимости с параметром
,
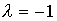что, вообще говоря, не вызывает затруднений.
С учетом (5.23) можно принять
,
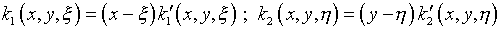где
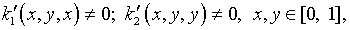
воспользовавшись выражениями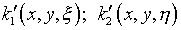 
для преломления априорной информации о решении с целью сглаживания
искомых функций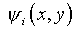 
и в целом упрощения процедуры вычислений. Понятно, что отмеченный
момент актуален для более сложных задач с различного рода особенностями
поведения решений и здесь мы упомянули о нем лишь в интересах общей
констатации.
Подстановка выражений (5.24), (5.25) в (5.21) порождает
систему интегральных уравнений
,
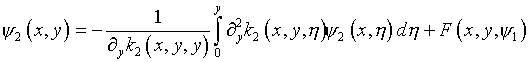(5.28)
где
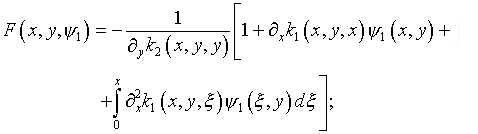
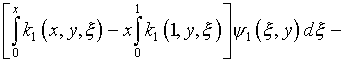
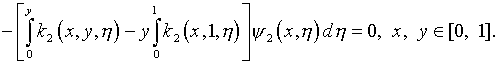(5.29)
Из уравнения (5.28)
,
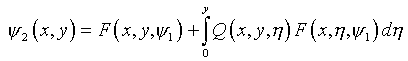(5.30)
где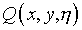 
– резольвента ядра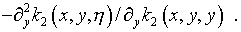 
Подстановка выражения (5.30) в (5.29) приводит к
интегральному уравнению Фредгольма первого рода относительно функции
.
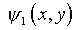Изложенная процедура непосредственно распространяется
на дифференциальные уравнения других типов, в подтверждение чего
рассмотрим простейшую задачу теплопроводности:
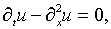(5.31)
.
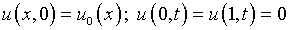(5.32)
Из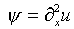 
,
уравнения (5.31) и условий (5.32) следует
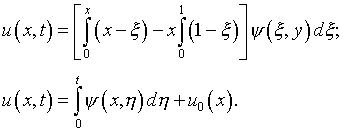
Соответственно
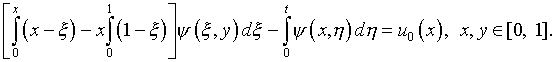
В целях аналогичного сведения задачи изгиба прямоугольной
пластины переменной жесткости D, защемленной вдоль контура
[7]:
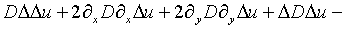
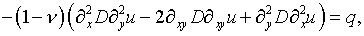(5.33)
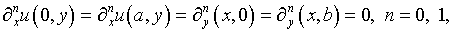(5.34)
где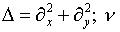 
– коэффициент Пуассона; 
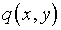– интенсивность поперечной нагрузки, для вычисления производных
по x можно принять
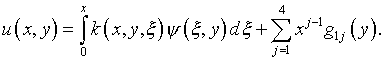(5.35)
Здесь
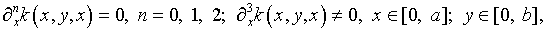
функции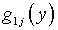 
предназначены для удовлетворения условий (5.34) при x = 0,
x = a.
Второе представление решения через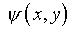
определяется посредством подстановки (5.35) в уравнение (5.33) и
четырехкратного интегрирования по переменной y. Возникающие
при этом функции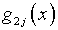 
позволяют удовлетворить условия (5.34) пр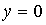и 
и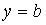 
,
после чего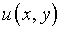 
из представлений решения исключается.
Кстати, с помощью специальной структуры ядра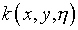 
несложно удовлетворить условия в отдельных точках внутри рассматриваемой
области, типа 
.
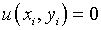Процедура сведения распространяется также на собственно смешанные
граничные условия (изменение типа вдоль стороны) и случай сопряжения
пластин. По аналогичной схеме к интегральным уравнениям Фредгольма
первого рода могут приводиться и трехмерные задачи математической
физики.
