5.4. Сопряжение с алгоритмом предыдущего раздела
Интегральные уравнения Фредгольма первого рода,
возникающие в случае оговоренного приведения двумерных краевых задач,
можно представить в виде
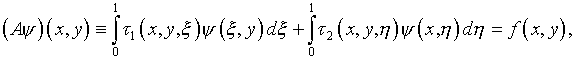
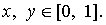(5.36)
Характерные разрывы ядер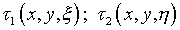 
на диагоналях 
,
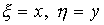как и другие подобные обстоятельства не имеют принципиального значения.
Алгоритм п.4 не претерпевает в данном случае сколько-нибудь
существенных изменений. Отличительные моменты связаны только лишь
со структурой оператора А. Аналог системы интегральных уравнений
Фредгольма второго рода (4.37) и (4.45) приобретает вид
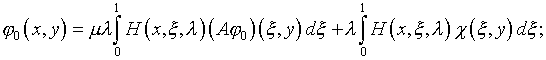(5.37)
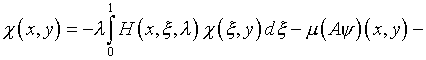
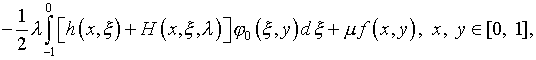
где
.
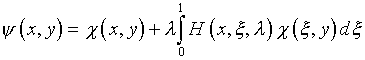(5.38)
При условии (4.47) с учетом (4.43), а также обозначений
(4.48) задача сводится к решению системы двумерных интегральных
уравнений Фредгольма второго рода
;
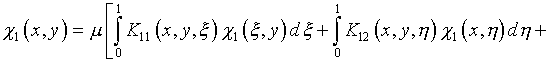
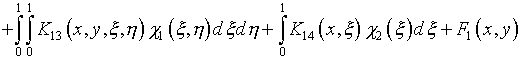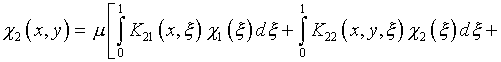
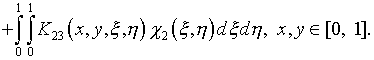
Здесь
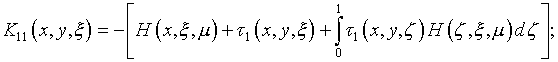
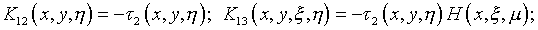
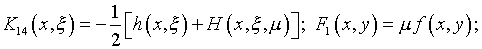
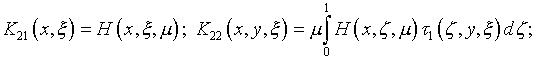
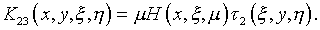
В дополнение (4.47), параметр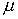 
не должен совпадать с характеристическими числами приведенной системы
уравнений. Для упрощения процедуры численной реализации его целесообразно
принять соответствующим условиям вида (4.55), (4.57).
Функция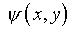 
,
удовлетворяющая уравнению (5.36) в смысле (4.59), находится по формуле
(5.38) с 
.
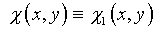Следует принять во внимание, что отмеченный в п.4.3 аппарат численной
реализации интегральных уравнений Фредгольма второго рода непосредственно
распространяется на рассматриваемый случай. При этом могут использоваться
специальные методы вычисления двумерных интегралов [14, п.3].
Литература к разделу
- Гурса Э. Курс математического анализа. – М.;
Л.: Гостехтеориздат, 1934. – Т.3. – Ч.2. – 318 с.
- Трикоми Ф. Интегральные уравнения. – М.: Изд-во
иностр. лит., 1960. – 299 с.
- Микеладзе Ш.Е. Новые методы интегрирования дифференциальных
уравнений и их приложения к задачам теории упругости. – М.; Л.:
Гостехтеориздат, 1951. – 291 с.
- Биргер И.А. Некоторые математические методы
решения инженерных задач. – М.: Оборонгиз, 1956. – 151 с.
- Голубенцев А.Н. Интегральные методы в динамике.
– Киев: Техніка, 1967. – 350 с.
- Медведев Ф.А. Очерки истории теории функций
действительного переменного. – М.: Наука, 1975. – 248 с.
- Тимошенко С.П., Войновский-Кригер С. Пластинки
и оболочки. – М.: Наука, 1966. – 635 с.
- Репман Ю.В. Общий метод расчета тонких плит
/Пластинки и оболочки. – М.;Л.: Госстройиздат, 1939. – С.149–179.
- Розин Л.А. Стержневые системы как системы конечных
элементов. – Л.: Изд-во Ленингр. ун-та, 1976. – 232 с.
- Габбасов Р.Ф. О численно-интегральном методе
решения краевых задач строительной механики для дифференциальных
уравнений в частных производных //Исследования по теории сооружений.
– М.: Стройиздат, 1976. – №22. – С.27–34.
- Алексидзе М.А. Фундаментальные функции в приближенных
решениях краевых задач. – М.: Наука, 1991. – 352 с.
- Белоцерковский С.М., Лифанов И.К. Численные
методы в сингулярных интегральных уравнениях. – М.: Наука, 1985.
– 256 с.
- Мюнтц Г. Интегральные уравнения. – Л.; М.: Гостехтеориздат,
1934. – 330 с.
- Крылов В.И., Шульгин Л.Т. Справочная книга по
численному интегрированию. – М.: Наука, 1966. – 370 с.
