-
ДРУГИЕ КЛАССЫ ЗАДАЧ
6.1. Начально-краевая задача для уравнения Кортевега-де
Вриза
Обратимся к постановке:
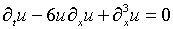 ,
(6.1)
,
(6.1)
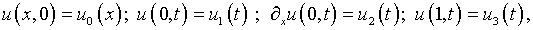 (6.2)
(6.2)
где функции 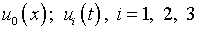 предполагаются заданными так, что не налагают каких-либо дополнительных
ограничений на модель рассматриваемого процесса.
предполагаются заданными так, что не налагают каких-либо дополнительных
ограничений на модель рассматриваемого процесса.
Следует принять во внимание, что сколько-нибудь
общая теория, которая позволяла бы априорно исследовать разрешимость
задач вида (6.1), (6.2) в адекватных для них классах функций, до
настоящего времени отсутствует. В этой связи основным средством
уточнения математической модели служат результаты численного эксперимента,
а также решения специальным образом упрощенных уравнений вблизи
границ (см. [1, п.10]).
Используя процедуру предыдущего раздела, нетрудно
произвести редукцию задачи (6.1), (6.2) к интегральному уравнению
первого рода относительно
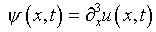 ,
,
откуда
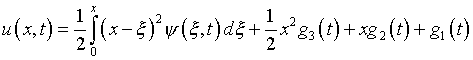 ,
(6.3)
,
(6.3)
где определяемые из граничных условий функции интегрирования
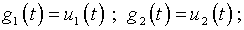
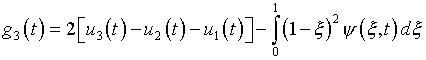 .
.
Подстановка в (6.3) приводит к выражению
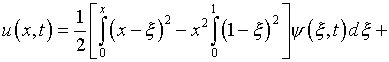
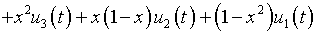 .
(6.4)
.
(6.4)
Уравнение (6.1) представим в виде
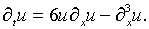 (6.5)
(6.5)
Подстановка (6.4) в правую часть (6.5) и интегрирование
от 0 до t с учетом начального условия (6.2) позволяет определить
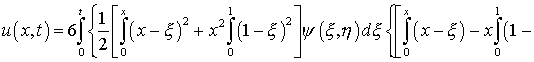
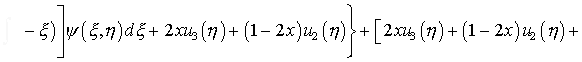
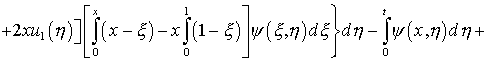
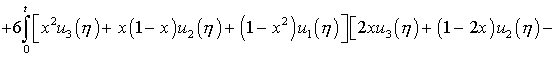
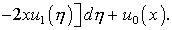 (6.6)
(6.6)
Исключая 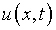 из (6.4), (6.6), получаем уравнение
из (6.4), (6.6), получаем уравнение
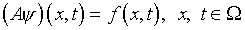
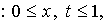 (6.7)
(6.7)
в котором выражения оператора А и свободного
члена f достаточно очевидны.
Пусть данные 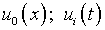 таковы, что
таковы, что 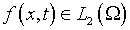 и, кроме того, решение задачи (6.1), (6.2) является
и, кроме того, решение задачи (6.1), (6.2) является 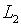 -функцией.
В этом случае, следуя п.4.1, можно воспользоваться соотношением
-функцией.
В этом случае, следуя п.4.1, можно воспользоваться соотношением
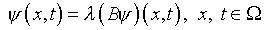 ,
,
где оператор В и параметр 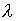 – те же.
– те же.
Алгоритм п.4.3 позволяет свести рассматриваемую
задачу к решению системы двух нелинейных интегральных уравнений
второго рода (5.37), в которой переменную y следует заменить
на t.
В силу непрерывной зависимости подынтегрального
выражения (6.6) от 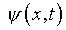 на основании принципа сжатых отображений при достаточно малом значении
параметра
на основании принципа сжатых отображений при достаточно малом значении
параметра 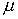 ,
удовлетворяющего условию (4.47), решение указанной системы уравнений
достигается методом простых итераций при произвольном выборе начальных
приближений из
,
удовлетворяющего условию (4.47), решение указанной системы уравнений
достигается методом простых итераций при произвольном выборе начальных
приближений из 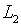 .
Оценка влияния погрешности вычислений, вопросы убыстрения сходимости
и другие аспекты численной реализации освещены в [2].
.
Оценка влияния погрешности вычислений, вопросы убыстрения сходимости
и другие аспекты численной реализации освещены в [2].
Следует подчеркнуть, что реализация условий сходимости
с помощью параметра 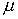 ,
позволяющая сравнительно простыми средствами определять, по существу,
частные решения, в нелинейном случае является особенно значимой.
Подразумевается, что другие решения могут устанавливаться в рамках
вычислительного эксперимента при больших
,
позволяющая сравнительно простыми средствами определять, по существу,
частные решения, в нелинейном случае является особенно значимой.
Подразумевается, что другие решения могут устанавливаться в рамках
вычислительного эксперимента при больших 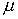 ,
связанного с исследованием неявных функций, разветвлений и бифуркаций.
,
связанного с исследованием неявных функций, разветвлений и бифуркаций.
Используя выражения (6.4), (6.6) решение можно представить
тождественно удовлетворяющим как начальному, так и граничным условиям
(6.2), а также оценить допускаемую погрешность по аналогии с изложенным
в п.5.2.

