ЗАКЛЮЧЕНИЕ

ЗАКЛЮЧЕНИЕ

Кратко подытожим изложенное выше. Итак, решение интегрального уравнения Фредгольма первого рода

(1)

в “удобном” для реализации вычислительных методов пространстве 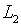, несомненно, представляет собой некорректно поставленную задачу. Ситуация с пространством 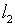является диаметрально противоположной: данные уравнения (1) могут удовлетворять условиям его корректности и, тем не менее, решение, определяемое по теореме Пикара, будет представлять ряд, расходящийся вследствие накопления погрешности округлений значащих цифр.

Следует принять во внимание, что даже собственно проверка принадлежности данных (1) пространству 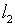, как правило, нереализуема. Кроме того, в качестве объективного фактора некорректности выступает погрешность экспериментального определения , а также и различные неточности идентификации исследуемой системы, то есть .

По существу, основу работы составляет предложение об адаптивной привязке уравнения (1) к пространству 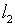путем использования функциональной модели допускаемой погрешности, включая сглаживание информации процедурой интегрирования, характеризующееся условием

(2)

Вначале из эвристических соображений, а затем и более основательно аргументирована целесообразность представления погрешности разностью искомой функции в явном виде и интегральной компоненты:

так, чтобы удовлетворение (2) осуществлялось посредством

В развитие выдвинутой концепции, постановка рассматриваемой задачи была подвергнута трансформации:

(3)

(4)

(5)

Здесь

При этом решение интегрального уравнения Фредгольма второго рода (3), выраженное через резольвенту ядра , собственно говоря, является определяющей предпосылкой достижения преследуемой цели, поскольку на и содержит функцию соответственно в явном виде и подынтегрально:

(6)

(7)

Далее с использованием данных задачи (1), что существенно, мы выразили посредством интегрирования функцию , являющуюся решением интегрального уравнения Фредгольма второго рода (4) при , а также

Из интегрального уравнения Фредгольма второго рода (5) появилось новое представление искомого решения через :

, (8)

меру нетождественности которого (6) как раз и отражает погрешность . Таким образом, решение задачи (1), понимаемое в смысле

, (9)

оказалось возможным определить выражениями принципиально различной структуры: с явно входящей функцией – (6) и без нее – (8).

Данное обстоятельство, предопределило сведение рассматриваемой задачи к решению интегрального уравнения Фредгольма второго рода

, (10)

где

(11)

путем подстановки выражений (6) – (8) в (4).

Структура уравнения (10) дает основание для следующей интерпретации. Вследствие (6), (11) и (9) получаемое в результате решение должно удовлетворять также и однородному уравнению

, (12)

естественно, с точностью, зависящей от 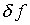. Это означает, что в процессе выкладок мы как бы выстраиваем ядро , для которого решение задачи является собственной функцией, причем уравнение (12) располагается на спектре.

Итак, традиционная постановка (1) преобразована в уравнение (10), предпочтительность которого определяется непрерывной зависимостью решения от данных задачи. Дополнительное преимущество состоит в возможности выбора параметра 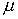из условия сходимости к решению простых итераций

Заметим, что ядро достаточно было наделить свойством полноты и вместе с тем весьма важными оказались его симметрия, зависимость от разности аргументов, а также периодичность, способствовавшие проведению выкладок в аналитической форме.

Показано, что к интегральным уравнениям Фредгольма первого рода сравнительно элементарным образом редуцируются широкие классы задач математического моделирования, после чего оговоренная процедура корректной постановки и численной реализации может быть распространена на них без существенных изменений. Кстати, при этом практически стирается традиционная дифференциация постановок задач математической физики на прямые и обратные. В условиях нелинейности, реализация итерационных алгоритмов решения получаемых интегральных уравнений посредством параметра 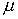является особенно значимой.

В свете изложенного можно сделать вывод о том, что если явление (процесс) допускает адекватное описание средствами математического моделирования, восстановление его побудительных причин, или же различных параметров по объективно достаточному объему дополнительной информации, не содержит принципиальных затруднений, поскольку соответствующие задачи могут быть поставлены корректно. С этой точки зрения, анализ реально наблюдаемых событий, включая многофакторные социально-экономические и экологические процессы, способен производиться с гораздо большей эффективностью.

Не следует ли предположить, что, вообще, процесс познания Мира значительно проще, нежели о нем принято судить в широкой аудитории под впечатлением отзвуков из сферы научного обслуживания, которая на современном этапе, вооружившись средствами электронной обработки информации, по существу предстает естественной монополией с едва ли не доминантной ролью коммерческого компонента, а соответственно и системной тягой к затратности?

Так, колоссальные средства расходуются на задачи восстановления зависимостей по эмпирическим данным и, в частности, дистанционное зондирование поверхности Земли средствами космического базирования. При этом фактически осуществляется эмпирический поиск минимально и максимально приемлемого значения параметра 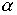в интегральном уравнении вида

Суть в необходимости установления паритета на стыке вычислительных и соответственно финансовых возможностей решения плохо обусловленной системы линейных алгебраических уравнений (подразумевается реализация одного из методов дискретизации) и приближения постановки рассматриваемой задачи к точной, которая ошибочно ассоциируется с фактором некорректности при .

Заметим в этой связи, что, конечно же, не следует полагать будто бы научные проблемы отсутствуют вообще, или же для их преодоления, независимо от обстоятельств, могут быть выработаны эффективные средства. Однако, по нашему мнению, осложнения принципиального характера присущи в первую очередь прямым постановкам отдельных задач, иначе говоря, построению математических моделей недостаточно изученных процессов и явлений.

Понятно, что при решении некоторых классов обратных задач математической физики также могут возникать весьма существенные препятствия и, тем не менее, распространенный тезис относительно некорректности процедуры восстановления причины по следствию в целом, представляется глубоко ошибочным.

Утверждение Ж.Адамара о корректности задач, адекватно описывающих реальные процессы, явилось гениальным предначертанием, конструктивное развитие которого позволит вывести потенциал средств математического моделирования на качественно более высокий уровень.

21 марта 2001 г.