6.7. Задача стефановского типа
Рассмотрим классическую модель [11]:
(6.29)
(6.30)
На движущейся границе, которая представляет собой
раздел фаз, задается дополнительное условие
(6.31)
где 
постоянная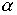 
может принимать как положительное, так и отрицательное значение;
.
Таким образом, данные задачи – 
и 
;
функци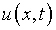и 
и 
подлежат определению.
В (6.29) – (6.31) целесообразно произвести неортогональное
отображение
(6.32)
на каноническую область 
Получаем
(6.33)
(6.34)
(6.35)
Аналогично предыдущему, из обозначения
условий (6.34) и уравнения (6.33) следует
(6.36)
(6.37)
Подстановка (6.36) в (6.35) дает
откуда
(6.38)
Соответственно в выражении (6.37)
.
Исключение 
из (6.36), (6.37) приводит к интегральному уравнению первого рода
(6.7), о решении которого было сказано выше. Найденную из него функцию
следует аппроксимировать аналитической зависимостью по 
для проведения обратной замены переменных. При этом искомая граница
определяется из нелинейного интегрального уравнения (6.38). Наконец,
по формулам (6.36), (6.37) с учетом (6.32) вычисляется функция .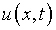
Литература к разделу
- Додд Р., Эйлбек Дж., Гиббон Дж., Моррис Х. Солитоны
и нелинейные волновые уравнения. – М.: Мир, 1988. – 694 с.
- Приближенное решение операторных уравнений /М.А.Красносельский,
Г.М.Вайникко, П.П.Забрейко и др. – М.: Наука, 1969. – 455 с.
- Погорелов А.В. Монжа – Ампера уравнение /Математическая
энциклопедия. – М.: Советская энциклопедия, 1982. – Т.3. – С.800–801.
- Бакельман И.Я. Геометрические методы решения
эллиптических уравнений. – М.: Наука, 1965. – 340 с.
- Коздоба Л.А. Методы решения нелинейных задач
теплопроводности. – М.: Наука, 1975. – 227 с.
- Пасконов В.М., Полежаев В.И., Чудов Л.А. Численное
моделирование процессов тепло- и массообмена. – М.: Наука, 1984.
– 285 с.
- Найфэ А. Введение в методы возмущений. – М.:
Мир, 1984. – 535 с.
- Ворожцов Е.В., Яненко Н.Н. Методы локализации
особенностей при численном решении задач гидродинамики. – Новосибирск:
Наука, 1985. – 224 с.
- Смирнов М.М. Уравнения смешанного типа. – М.:
Наука, 1970. – 295 с.
- Романов В.Г. Обратные задачи математической физики.
– М.: Наука, 1984. – 263 с.
- Рубинштейн Л.И. Проблема Стефана. – Рига: Звайгзне,
1967. – 457 с.
