6.6. Обратная задача о восстановлении коэффициента
дифференциального уравнения
Малые колебания в поперечном направлении растянутой
струны переменной плотности описываются уравнением
(6.24)
Здесь x, t – безразмерные координаты;
где N – натяжение; 
– плотность материала; 2l – длина струны; Т – временной
интервал.
Предполагается, что края струны закреплены и ее
плотность, а также колебания симметричны относительно координаты
x = 0. При этом граничные условия имеют вид
(6.25)
Используем также начальные условия
(6.26)
Необходимо определить коэффициент 
на основании (6.24) – (6.28) при данных 
и дополнительной информации о колебаниях среднего сечения струны
.
(6.27)
Известно [10], что решение сформулированной задачи
может существовать и являться единственным в классах функций, вполне
адекватных методу насто-ящей работы. Будем считать необходимые в
этом смысле требования выполненными.
По аналогии с неоднократно проделанным выше, используя
обозначение (6.16) и (6.24) – (6.26), находим представления
(6.28)
Исключая из них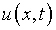 
,
получаем уравнение вида (6.7). Подстановка (6.28) в (6.27) приводит
к интегральному уравнению
где
О сходимости последовательных приближений к решению
сформированной таким образом системы уравнений можно судить по сглаживанию
зависимости коэффициента а от значений t в процессе
вычислений.
