6.5. Уравнение смешанного типа
Краевые задачи для таких уравнений характерны нетривиальностью
исследования вопросов существования и единственности решений (см.
[9]). Вследствие этого их приходится рассматривать в областях весьма
специального вида, что сужает круг практических приложений.
В качестве иллюстрации обратимся к известному уравнению
Трикоми
(6.21)
которое является гиперболическим и эллиптическим
соответственно при y < 0 и y
> 0. Ограничиваясь рамками вычислительного эксперимента,
то есть не рассматривая априори разрешимость задачи, используем,
например, следующие граничные условия
(6.22)
где функция 
задана так, что 
.
Обозначим
,
(6.23)
откуда с учетом (6.22)
.
Двукратное интегрирование уравнения (6.21) в пределах
–1, y с учетом (6.23) и (6.22) приводит к выражению
Задача сводится к решению интегрального уравнения
Фредгольма второго рода (6.13) в области 
с оператором
и свободным членом
.
Отметим естественное выполнение так называемого
условия склеивания на линии параболического вырождения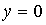 
,
которое предъявляется к решению уравнения (6.21) [9, c.27]:
Как и в предыдущем подразделе, данное обстоятельство
обуславливается переведением особенности задачи от главного члена
описывающего его оператора к подчиненному.
