6.4. Малый параметр при старшей производной дифференциального
уравнения задачи
Общие соображения проиллюстрируем задачей о распространении
тепла, обусловленном процессами теплопроводности и конвекции (соответственно
первое и второе слагаемое правой части дифференциального уравнения)
[6]:
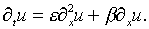(6.17)
Здесь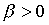 
– постоянная; 
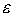– малый параметр,
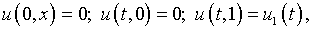(6.18)
где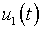 
– данная функция.
Из обозначения (6.16) с учетом граничных условий
(6.18) вытекает
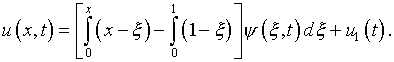(6.19)
Интегрирование (6.17) в пределах 0, t с использованием
(6.19) и начального условия (6.18) дает
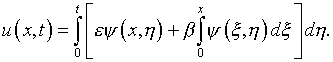
Задача сводится к линейному интегральному уравнению
первого рода (6.7), в котором
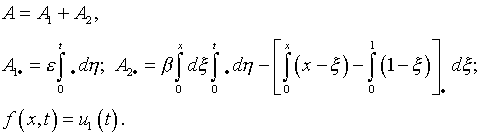
Алгоритм п.4 позволяет перейти к интегральному уравнению
Фредгольма второго рода
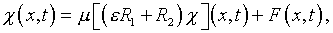(6.20)
где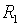 
и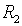 
– соответствующие операторы.
В результате разложения [7]
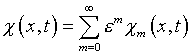
возникает последовательность рекуррентных соотношений
…
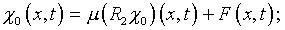
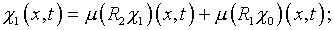
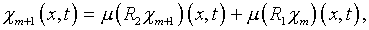
представляющих собой интегральные уравнения того
же типа канонической структуры.
На основании изложенного, следует констатировать,
что предлагаемый подход весьма эффективен в задачах математической
физики с сингулярным возмущением, численная реализация которых,
как правило, встречает существенные осложнения (см., в частности,
[8]). Действительно, сингулярное возмущение (6.17) оказалось возможным
перевести в регулярное (6.20), что способствовало радикальному упрощению
задачи *.
| * Согласно принятой классификации, сингулярные и регулярные
возмущения воздействуют со-ответственно на главные и подчиненные
члены операторов. |
