2. СУЩЕСТВУЮЩИЕ ПОДХОДЫ К РЕШЕНИЮ НЕКОРРЕКТНЫХ
ЗАДАЧ
2.1. Методология А.Н.Тихонова
Изложение данного подраздела базируется на материалах монографии
А.Н.Тихонова и В.Я.Арсенина [1], которую буквально пронизывает концепция
адекватности некорректных постановок и, в частности, интегральных
уравнений первого рода задачам математической физики. В качестве
иллюстрации показано, что решение интегрального уравнения Фредгольма
первого рода
 (2.1)
(2.1)
с 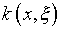 и
и 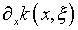 непрерывными по x может претерпевать сколь угодно значительные
изменения как в метрике C, так и L2 при
малых в
непрерывными по x может претерпевать сколь угодно значительные
изменения как в метрике C, так и L2 при
малых в  вариациях правой части вида
вариациях правой части вида

Ситуация с возмущением ядра  по существу аналогична, в связи с чем авторы ставят вопрос: что
следует понимать под решением уравнения (2.1), когда k и
f известны приближенно? По их мнению, подобная задача должна
рассматриваться как “недоопределенная” и соответственно для отбора
возможных решений необходимо привлекать дополнительную информацию
о функции
по существу аналогична, в связи с чем авторы ставят вопрос: что
следует понимать под решением уравнения (2.1), когда k и
f известны приближенно? По их мнению, подобная задача должна
рассматриваться как “недоопределенная” и соответственно для отбора
возможных решений необходимо привлекать дополнительную информацию
о функции  качественного, или же количественного характера, которая “обычно”
имеется. В этой связи обратим внимание на соображения Н.Г.Преображенского
относительно системы линейных алгебраических уравнений, получаемой
дискретизацией (2.1) [2, c.130]:
качественного, или же количественного характера, которая “обычно”
имеется. В этой связи обратим внимание на соображения Н.Г.Преображенского
относительно системы линейных алгебраических уравнений, получаемой
дискретизацией (2.1) [2, c.130]:
“Анализ показывает, что выбирая достаточно высокий порядок приближения
мы превращаем [указанную систему] в сколь угодно плохо обусловленную…
В этих условиях необходимо внесение в алгоритм какой-либо априорной
нетривиальной дополнительной информации, с помощью которой только
и можно надеяться отфильтровать вуалирующие ложные варианты и выделить
решение, наиболее близкое к истинному. Любые чисто математические
ухищрения, не привлекающие дополнительных априорных данных, эквивалентны
попытке создания информационного perpetuum mobile, производящего
информацию из ничего”.
На априорной количественной информации основывается так называ-емый
метод подбора решения некорректно поставленных задач. Показано,
что если компакт М метрического пространства Е1
взаимно однозначно и непрерывно отображается на множество F
метрического пространства Е2, то обратное отображение
F на М также непрерывно. Соответственно предположение
о принадлежности решения, в частности, уравнения (2.1) компакту
М позволяет считать оператор А-1 на множестве
F = AM непрерывным. Практическая реализация сводится к аппроксимации
М рядом с параметрами, изменяющимися в ограниченных пределах
(так, чтобы М представляло замкнутое множество конечномерного
пространства), которые находятся из условия минимизации невязки
удовлетворения (2.1). Отметим отсутствие сколько-нибудь общих рекомендаций
в отношении выбора М.
В свете изложенного, М.М.Лаврентьев сформулировал понятие корректности
по Тихонову для уравнения вида (2.1) с функциями y и f,
принадлежащими банаховым пространствам соответственно В1
и В2 [3]:
- Априори известно, что решение рассматриваемого уравнения
 существует
и принадлежит множеству М пространства В1.
существует
и принадлежит множеству М пространства В1.
- Решение
 единственно на множестве М.
единственно на множестве М.
- Оператор А-1 непрерывен на множестве АМ
пространства В2.
Если М – компакт (случай назван “обычным”)
последнее условие становится следствием предыдущих.
Оператор  назван регуляризирующим для уравнения (2.1), в случае если
он обладает свойствами:
назван регуляризирующим для уравнения (2.1), в случае если
он обладает свойствами:
- Определен для любых a > 0 и fÎ E2.
- При
 ,
где
,
где  и
и  – соответствующие точные выражения, существует такое
– соответствующие точные выражения, существует такое  ,
что для любого
,
что для любого  найдется
найдется  .
Здесь
.
Здесь  .
.
Подразумевается возможность выбора  так, что при
так, что при  регуляризованное решение
регуляризованное решение  ,
то есть
,
то есть  .
Вместе с тем отмечена алгоритмическая сложность построения зависимости
.
Вместе с тем отмечена алгоритмическая сложность построения зависимости
 ,
для которой оператор
,
для которой оператор  являлся бы регуляризирующим, применительно к классам практически
важных задач. Вопросам разрешения данной ситуации посвящены многочисленные
публикации последователей А.Н.Тихонова, о которых будет сказано
ниже.
являлся бы регуляризирующим, применительно к классам практически
важных задач. Вопросам разрешения данной ситуации посвящены многочисленные
публикации последователей А.Н.Тихонова, о которых будет сказано
ниже.
Непосредственно в [1], построение  выполнено с привлечением аппарата вариационного исчисления, сводящего
вычисление
выполнено с привлечением аппарата вариационного исчисления, сводящего
вычисление  к минимизации функционала
к минимизации функционала
 .
(2.2)
.
(2.2)
Для уравнения (2.1) его стабилизирующую компоненту рекомендовано
использовать в виде
 (2.3)
(2.3)
где p0, p1 ³ 0 – заданные
функции.
В случае симметричного ядра 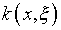 процедура минимизации эквивалентна решению интегро-дифференциального
уравнения
процедура минимизации эквивалентна решению интегро-дифференциального
уравнения
 (2.4)
(2.4)
при условиях
 .
(2.5)
.
(2.5)
Здесь  – произвольная вариация функции
– произвольная вариация функции  ,
не выводящая ее из класса допустимых.
,
не выводящая ее из класса допустимых.
По мнению авторов [4], подавляющее большинство обратных задач являются
некорректно поставленными, причем попытки их решения, ввиду огромной
практической важности, предпринимались на протяжении длительного
периода. “Но только в результате … появления фундаментальных работ
академика А.Н.Тихонова была создана современная теория решения обратных
задач, в основу которой легло понятие регуляризующего алгоритма”
(с.7). Далее продемонстрирована эффективность процедуры численной
реализации интегральных уравнений Фредгольма первого рода, связанных
с интерпретацией астрофизических наблюдений, посредством выделения
компакта возможных решений в классе монотонно ограниченных функций.
Как отметил О.А.Лисковец [5]: “… корректность по Тихонову достигается
за счет сужения допустимого множества решений до класса корректности”
(с.13). Представляет интерес также следующая выдержка из указанной
монографии: “В отличие от господствовавшего прежде мнения о том,
что все задачи, описывающие физическую реальность, корректны, по
современным представлениям каждая реальная задача регуляризуема,
то есть имеет хотя бы один регуляризатор” (с.14).
Приведем заключение В.А.Морозова [6, c.9]: “Метод регуляризации
А.Н.Тихонова оказался необременительным на практике, так как не
требовал фактического задания компакта М, в котором содержится искомое
решение уравнения (2.1). … Основная трудность применения данного
метода заключается в формулировке алгоритмических принципов выбора
параметра регуляризации a ”. Из его же монографии [7, c.4]:
“Значимость статьи А.Н.Тихонова [8] трудно переоценить. Она послужила
толчком для выполнения целого ряда работ других исследователей в
самых различных областях математического анализа и естествознания:
спектроскопии, электронной микроскопии, идентификации и автоматическом
регулировании, гравиметрии, оптике, ядерной физике, физике плазмы,
метеорологии, автоматизации научных исследований и ряде других разделов
науки и техники”.
Достаточно характерны соображения В.В.Воеводина [9]: “Успех применения
метода регуляризации к решению неустойчивых систем алгебраических
уравнений объясняется в значительной мере тем, что А.Н.Тихонов и
его последователи не ограничились исследованиями отдельных фрагментов
этой сложной задачи, а рассмотрели весь комплекс связанных с ней
вопросов. Это в первую очередь четкая постановка самой задачи, построение
устойчивого к возмущению входных данных алгоритма ее решения, разработка
эффективного численного метода, получение оценок отклонения реально
вычисляемого объекта от искомого в зависимости от возмущения входных
данных и ошибок округления”.
Из предисловия к сборнику [9] А.А.Самарского и А.Г.Свешникова: “Фундаментальное
значение для всей современной математики имеет выяснение Андреем
Николаевичем Тихоновым роли некорректных задач в классической математике
и ее приложениях (обратные задачи). Им предложен принципиально новый
подход к этому классу задач и развиты методы построения их устойчивых
решений, основанные на принципе регуляризации”.

