2.2. Краткий экскурс в
развитие обозначенных концепций
Результаты исследований,
посвященных установлению параметра регуляризации a,
подытожены в [10]. В предположении о том, что погрешности определения
свободного члена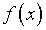 
и ядра 
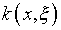уравнения (2.1) известны, используются различные принципы минимизации
невязки вида
При этом вычисление параметра
a как корня соответствующего уравнения
не вызывает затруднений, однако выбор m
, по существу, сопряжен со значительной неопределенностью. Главное
препятствие состоит в том, что весьма проблематичной является достоверная
оценка погрешности, обусловленной несовместностью конкретно рассматриваемого
уравнения 
Значительные усилия предпринимались
с целью сокращения объема информации, необходимой для вычисления
параметра a . Заметный шаг в этом
направлении сделан А.Н.Тихоновым и В.Б.Гласко, предложившими критерий
минимизации по a >
0 функционала 
[11] (см. также [1,
п.2.7]), однако его теоретическое обоснование оказалось возможным
лишь для сравнительно узких классов задач. Ряд способов определения
a связан с использованием решений
уравнения (2.1) для выражений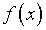
специального вида.
В [10] освещено также состояние
исследований по оценке точности методов решения интегрального уравнения
(2.1). При этом в случае принадлежности 
компакту серьезных осложнений, как правило, не возникает и основной
интерес представляет алгоритм регуляризации. Если в (2.3)
p1º0 и
параметр a
– конечен, (2.4) становится
интегральным уравнением Фредгольма второго рода, на которое, в предположении
известной погрешности определения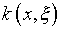 
и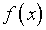 
,
распространяется общая теория приближенных методов Л.В.Канторовича
[12, п.14.1].
Вместе с тем, как показал
В.А.Винокуров [13], при отсутствии априорной информации о решении
уравнения (2.1) оценка погрешности вычисления 
средствами регуляризации принципиально неосуществима. Правомерна
лишь постановка вопроса о сходимости вычислительной процедуры, или
же регуляризуемости соответствующей задачи.
Отметим в этой связи соображение
А.Б.Бакушинского и А.В.Гончарского [14, c.13]: “К сожалению, в общем
случае невозможно оценить меру близости 
к 
без
дополнительной информации о решении уравнения (2.1). Это характерная
особенность некорректных задач. В общем случае регуляризирующий
алгоритм гарантирует лишь асимптотическую сходимость приближенного
решения к точному при 
”.
С именем М.М.Лаврентьева
связывают фактически частный случай практической реализации метода
А.Н.Тихонова, состоящий в сведении задачи (2.4), (2.5) к решению
интегрального уравнения Фредгольма второго рода
(2.6)
где a
> 0 – малый
параметр.
Показано, что 
при 
и 
.
Здесь g –
погрешность в определении ядра ,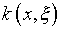
аналогичная d (см. п.2.1).
Метод В.К.Иванова [15] позволяет
находить так называемое квазирешение, минимизирующее невязку удовлетворения
(2.1) для класса функций 
,
где 
– компакт, условия определения которого, вообще говоря, созвучны
используемым в теореме Пикара (см. п.1.2). Квазирешение уравнения
(2.1) на таком компакте имеет вид
(2.7)
Здесь
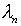и 
– соответственно характеристические числа и собственные функции
ядра ;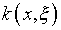
параметр l =
0 и представляет положительный
корень уравнения
(2.8)
при условиях соответственно
(2.9)
Специальные методы регуляризации
разработаны для ситуаций, при которых о решении уравнений вида (2.1)
имеется значительный объем информации статистического характера
(спектральные плотности, математические ожидания и т.п.). Так, В.Н.Вапник
[16] вполне конструктивно использовал специфику задач о распознавании
образов, связанную с неоднозначностью и вследствие этого экстремальным
поведением искомых функций. Обратим внимание на приведенное в указанной
монографии определение (с.8), которое, по всей видимости, подразумевалось
многими, однако не находило столь отчетливой формулировки.
“Задача восстановления зависимостей
по эмпирическим данным была и, вероятно, всегда будет центральной
в прикладном анализе. Эта задача является математической интерпретацией
одной из основных проблем естествознания: как найти существующую
закономерность по разрозненным фактам”.
